 |
Экспоненциальное сглаживание
|
|
|
|
Для экспоненциального сглаживания ряда используется рекуррентная формула:
(6.1)
где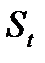 
- значение экспоненциальной средней в момент t;
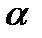- параметр сглаживания, 
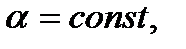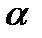0< <1;
.
Если последовательно использовать соотношение (7.1), то экспоненциальную среднюю 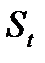можно выразить через предшествующие значения уровней временного ряда:
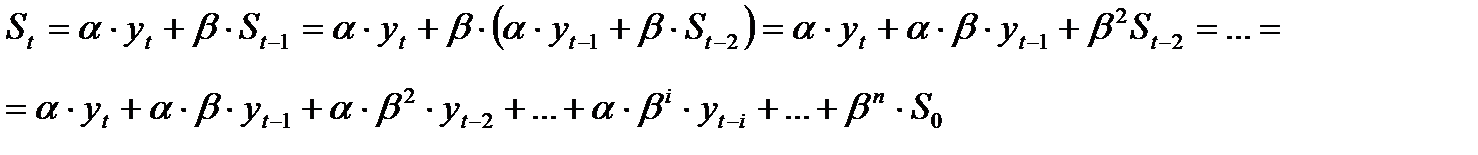
Таким образом,
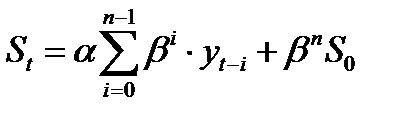(6.2)
где n – длина ряда.
При 
, следовательно,
(6.3)
Таким образом, величина 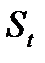оказывается взвешенной суммой всех членов ряда. Причем веса отдельных уровней ряда убывают по мере их удаления в прошлое соответственно экспоненциальной функции (в зависимости от «возраста» наблюдений). Именно поэтому величина 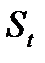называется экспоненциальной средней.
Автор модели английский математик Р. Браун показал, что математическое ожидание ВР и экспоненциальной средней совпадут, но в то же время дисперсия экспоненциальной средней D[ 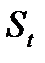] меньше дисперсии ВР 
:
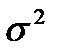(6.4)
Так как 0< 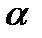<1, D[ 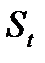] меньше дисперсии временного ряда, равной .
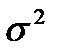При высоком значении 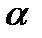дисперсия экспоненциальной средней незначительно отличается от дисперсии ряда. С уменьшением 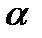дисперсия экспоненциальной средней сокращается, возрастает ее отличие от дисперсии ряда. Тем самым экспоненциальная средняя начинает играть роль «фильтра», поглощающего колебания временного ряда.
Таким образом, с одной стороны, следует увеличивать вес более свежих наблюдений, что может быть достигнуто повышением 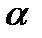, с другой стороны, для сглаживания случайных отклонений значение 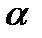нужно уменьшить. Эти два требования находятся в противоречии. Поиск компромиссного значения параметра сглаживания 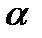составляет задачу оптимизации модели. При краткосрочном прогнозировании желательно как можно быстрее отразить изменения ряда и в то же время очистить ряд, отфильтровав случайные колебания. Для этого величине 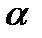следует присваивать одно из промежуточных значений от 0 до 1. При этом для оперативных, конъюнктурных прогнозов в большей степени должна учитываться свежая информация, поэтому 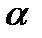следует брать большим. При увеличении срока прогнозирования 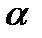следует уменьшить. В некоторых работах приводится формула для расчета :
|
|
|
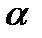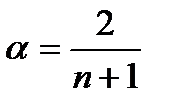, (6.5)
где n – длина ряда.
При расчете экспоненциальной средней в момент времени t всегда требуется значение экспоненциальной средней в предыдущий момент времени. Часто на практике в качестве начального значения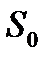 
используется среднее арифметическое значение из всех имеющихся уровней ВР или из какой-то их части.
При использовании экспоненциальной средней для краткосрочного прогнозирования предполагается, что модель ряда имеет вид:
, (6.6)
где 
– варьирующий во времени средний уровень временного ряда;
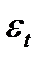– случайные неавтокоррелированные отклонения с нулевым мат. ожиданием и дисперсией .
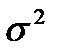Прогнозная модель определяется равенством:
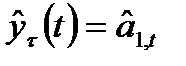, (6.7)
где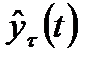 
- прогноз, сделанный в момент t на 
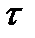единиц времени вперед;
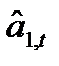– оценка .
Единственный параметр модели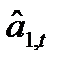 
определяется экспоненциальной средней:
= ;
= 
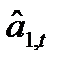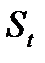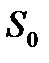
Выражение (1) можно представить по другому, перегруппировав члены:
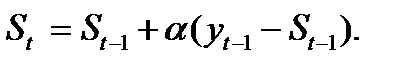(6.8)
Величину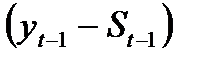 
можно рассматривать как погрешность прогноза. Тогда новый прогноз 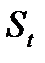получается в результате корректировки предыдущего прогноза с учетом его ошибки. В этом и состоит адаптация модели[19].
Вопросы для самоконтроля:
1 Укажите характерные особенности адаптивных методов прогнозирования.
2 Какие типы адаптивных моделей вы знаете?
3 Чем объясняется название «экспоненциальная средняя»?
4 Какую роль играет параметр адаптации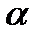 
в процедуре экспоненциального сглаживания?
|
|
|
5 Как влияет значение параметра адаптации 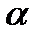на характер ряда, полученного после экспоненциального сглаживания?
Глава 7
_________________________________________________________________
Моделирование и прогнозирование временного ряда с помощью ARMA- и ARIMA- процессов _________________________________________________________________
7.1. Стационарные ВР и их основные характеристики.
7.2. Модели стационарных временных рядов.
7.3. Прогнозирование ARMA – процессов.
7.4. Методология Бокса – Дженкинса.
|
|
|
