 |
Моделирование сезонных колебаний с помощью фиктивных переменных
|
|
|
|
Рассмотрим ещё один метод моделирования ВР, содержащего сезонные колебания, – построение модели регрессии с включением фактора времени и фиктивных переменных.
Количество фиктивных переменных в такой модели должно быть на единицу меньше числа моментов (периодов) времени внутри одного цикла колебаний. Каждая фиктивная переменная отражает сезонную (циклическую) компоненту ВР для какого – либо одного периода. Она равна 1 для данного периода и нулю для всех остальных.
Пусть имеется временной ряд, содержащий циклические колебания периодичностью К.Модель регрессии с фиктивными переменными для этого ряда:
(5.33)
где 
Например, при моделировании сезонных колебаний на основе поквартальных данных за несколько лет число кварталов внутри одного года K=4, а общий вид модели:
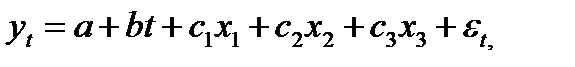(5.34)
где 
(5.35)
(5.36)
(5.37)
Уравнение тренда для каждого квартала будет иметь следующий вид:
для 1 квартала: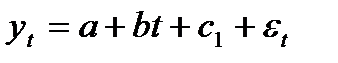 
(5.38)
для 2 квартала: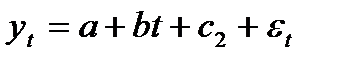 
(5.39)
для 3 квартала: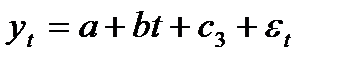 
(5.40)
для 4 квартала: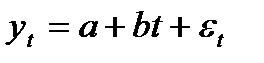 
(5.41)
Таким образом, фиктивные переменные позволяют дифференцировать величину свободного члена уравнения регрессии для каждого квартала. Она составит:
для 1 квартала (а+с1) (5.42)
для 2 квартала (а+с2) (5.43)
для 3 квартала (а+с3) (5.44)
для 4 квартала а (5.45)
Параметр b в этой модели характеризует среднее абсолютное изменение уровней ряда под воздействием тенденции.
Вопросы для самоконтроля:
1 Что понимается под сезонными колебаниями?
2 Расскажите методику построения аддитивной модели сезонности.
3 Расскажите методику построения мультипликативной модели сезонности.
4 В чем суть спектрального анализа?
5 Как проводится моделирование сезонных колебаний с помощью фиктивных переменных?
|
|
|
Глава 6
_________________________________________________________________
Моделирование и прогнозирование временных рядов с помощью адаптивных методов прогнозирования _________________________________________________________________
6.1. Сущность адаптивных методов.
6.2. Экспоненциальное сглаживание.
6.1 Сущность адаптивных методов
В настоящее время одним из наиболее перспективных направлений исследования и прогнозирования одномерных временных рядов считаются адаптивные методы.
Адаптивными называются методы прогнозирования, позволяющие строить самокорректирующиеся (самонастраивающиеся) экономико-математические модели, которые способны оперативно реагировать на изменение условий путем учета результата прогноза, сделанного на предыдущем шаге, и учета различной информационной ценности уровней ряда.
При обработке временных рядов, как правило, наиболее ценной бывает информация последнего периода, т.к. необходимо знать, как будет развиваться тенденция, существующая в данный момент, а не тенденция, сложившаяся в среднем не всем рассматриваемом периоде. Адаптивные методы позволяют учесть различную информационную ценность уровней ВР, степень «устаревания» данных.
Прогнозирование методом экстраполяции на основе кривых роста в какой-то мере тоже содержат элемент адаптации, поскольку с получением «свежих» фактических данных параметры кривых пересчитываются заново. Поступление новых данных может привести и к замене выбранной ранее кривой на другую модель. Однако степень адаптации в данном случае весьма незначительна, кроме того, она падает с ростом длины временного ряда, т.к. при этом уменьшается «весомость» каждой новой точки. В адаптивных методах различную ценность уровней в зависимости от их «возраста» можно учесть с помощью системы весов, придаваемых этим уровням.
Важнейшее достоинство адаптивных методов – построение самокорректирующихся моделей, способных учитывать результат прогноза, сделанного на предыдущем шаге. Пусть модель находится в некотором состоянии, для которого определены текущие значения ее коэффициентов. На основе этой модели делается прогноз. При поступлении фактического значения оценивается ошибка прогнозного значения (разница между этим значением и полученным по модели). Ошибка прогнозирования через обратную связь поступает в модель и учитывается в ней в соответствии с принятой процедурой перехода от одного состояния в другое. В результате вырабатываются «компенсирующие» изменения, состоящие в корректировании параметров в целях большего согласования поведения модели с динамикой ряда. Затем рассчитывается прогнозная оценка на следующий момент времени, и весь процесс повторяется вновь.
|
|
|
Таким образом, адаптация осуществляется итеративно с получением каждой новой фактической точки ряда. Модель постоянно «впитывает» новую информацию, приспосабливается к ней и поэтому отражает тенденцию развития, существующую в данный момент.
Быстроту реакции модели на изменения в динамике процесса характеризует параметр адаптации. Он должен быть выбран таким образом, чтобы обеспечивалось адекватное отображение тенденции при одновременной фильтрации случайных отклонений. Значение параметра адаптации может быть определено:
· на основе эмпирических данных;
· выведено аналитическим способом;
· получено на основе метода проб.
В качестве критерия оптимальности при выборе параметра адаптации обычно
принимают критерий минимума среднего квадрата ошибок прогнозирования[18].
|
|
|
