 |
Методология Бокса – Дженкинса
|
|
|
|
Экономические временные ряды за редким исключением нестационарны. Нестационарность чаще всего проявляется в наличии зависящей от времени неслучайной составляющей f(t). Для описания таких рядов используется модель авторегрессии – проинтегрированного скользящего среднего ARIMA (p,d,q) (модель Бокса-Дженкинса).
Модель ARIMA используется для описания временных рядов, обладающих свойствами:
1. ряд включает аддитивно составляющую f(t), имеющую вид алгебраического полинома;
2. ряд, получившийся после применения к нему процедур последовательных разностей, может быть описан моделью ARMA (p,q).
Пусть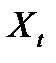 
- нестационарный процесс со стационарными разностями d - го порядка, т.е. 
- стационарный процесс, а 
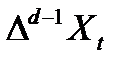- нестационарный. Это означает, что 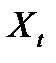интегрируем d - го порядка.
Если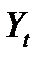 
- процесс ARMA (p,q), т.е.
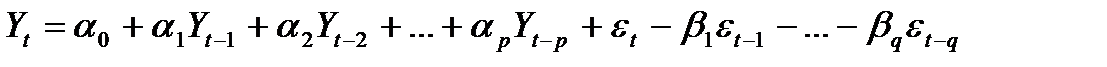, (7.28)
тогда 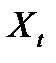называется процессом ARIMA (p,d,q). Часто среднее или свободный член приравнивается к нулю (опускается)[24].
Построение модели ARIMA по реализации случайного процесса Бокс и Дженкинс предложили разбить на несколько этапов:
1. Устанавливается порядок интеграции d, т.е. добиться стационарности ряда, взяв достаточное количество последовательных разностей. Для определения значения d может быть применен эвристический критерий. Использование данного критерия основано определении оценки
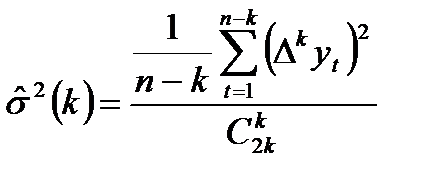, (7.29)
где 
- последовательные разности исходного ряда 
,
k – порядок разностей, k = 1,2,…
Начиная с некоторого значения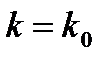 
величина 
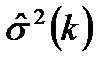стабилизируется, оставаясь примерно на одном и том же уровне при росте k. Тогда порядок разности 
следует принять равным 
.
Также о том, что необходимая для стационарности ряда степень разности достигнут, будет свидетельствовать быстрое затухании АКФ.
|
|
|
2. Для полученного стационарного временного ряда строятся АКФ и ЧАКФ. Исследуя характер их поведения, выдвигаются гипотезы о значениях параметров p и q, т.е. подбирается модель ARMA(p,q). На данном этапе формируется базовый набор моделей, включающий 1,2 или даже больше количество моделей.
3. Для всех моделей, отобранных на 2 этапе оцениваются коэффициенты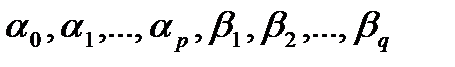 
, используя следующие методы:
· традиционный МНК;
· метод максимального правдоподобия;
· нелинейный МНК;
· алгоритм Марквардта.
Все эти оценки при больших объемах выборок асимптотически эквивалентны.
4. Выбирается наиболее подходящая модель среди оцененных:
а) проверяется адекватность модели на основе анализа остатков (у адекватной модели остатки должны быть похожи на белый шум). Для этого проводится проверка значимости коэффициентов автокорреляции используя следующие подходы:
· если выборочный коэффициент автокорреляции 
выходит за интервал 
, то гипотеза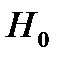 
о равенстве нулю коэффициента автокорреляции 
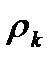отвергается;
· проверяется равенства нулю сразу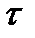 
первых значений АКФ на основе Q – статистики Бокса – Пирса:
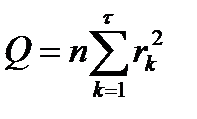(7.30)
или тест Бокса – Льюнга:
. (7.31)
Если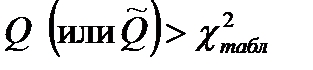 
с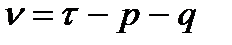 
степенями свободы, то как группа первые 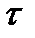коэффициентов автокорреляции значимы (рекомендуется рассматривать 
);
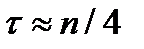б) отбирается оптимальная модель по наивысшему качеству с меньшим числом параметров с использованием информационного критерия Акайка и Шварца:
· информационный критерий Акайка
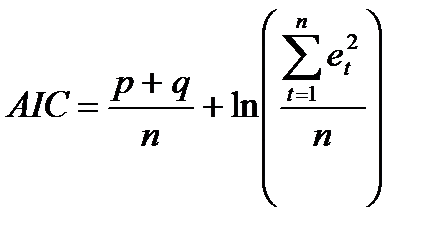; (7.32)
· критерий Шварца:
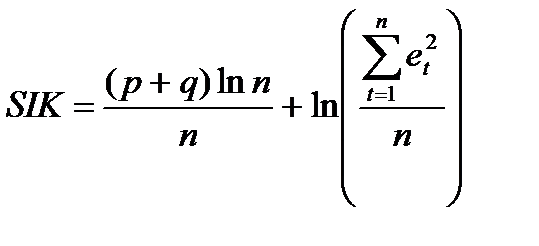(7.33)
Предпочтение следует отдать модели с меньшим значением критерия.
Прогнозирование ARIMA – процессов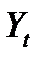 
может быть представлено в виде двухшаговой процедуры:
1) экстраполируется стационарный ARMA – процесс;
2) Вместо взятия разностей провести обратную операцию интегрируемости, т.е. суммирования спрогнозированных на шаге 1 приращений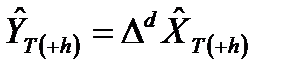 
, чтобы получить сначала 
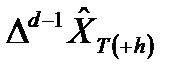, а затем по аналогии 
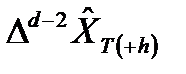и, наконец, 
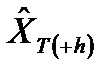. Оценка дисперсии ошибки прогноза, а следовательно, и ширины доверительного интервала прогноза проводится аналогичным образом – повторным суммированием дисперсий ошибок прогноза ARMA-процесса 
.
|
|
|
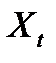Другим возможным вариантом является построение индивидуальной одношаговой формулы для получения прогноза.
С этой целью в уравнение вместо 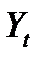подставляют разности
. (7.34)
Решив полученное уравнение относительно 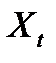, получим формулу которая может быть экстраполирована для 
и таким образом преобразована в формулу для прогнозирования на 
шагов вперед величин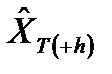 
с началом отсчета в момент времени Т.
Вопросы для самоконтроля:
1 Что такое стационарные временные ряды в широком и узком смысле?
2 Какие существуют классы моделей для прогнозирования стационарных временных рядов?
3 Как проводится идентификация AR(p) моделей с помощью анализа автокорреляционной и частной автокорреляционной функций?
4 Как проводится идентификация MA(q) моделей с помощью анализа автокорреляционной и частной автокорреляционной функций?
5 Назовите основные этапы построения модели ARIMA.
6 Какие критерии применяются при окончательном выборе модели ARIMA?
Глава 8
___________________________________________________________________
|
|
|
