Процентильная нормализация суммарных баллов

Экстра-версия Xj	Час- тота fj	Накоп-ленная частота Fj	Скор. накопл. част. F*j	Процен-тильный ранг PRj	s	zj
					-2,06	0,88
					-1,40	2,2
			6,5		-1,13	2,74
					-0,64	3,72
					-0,05	4,9
			35,5		0,56	6,12
					1,08	6,16
			47,5		1,64	8,28
			49,5		2,33	9.66

 

Б. Подсчитать накопленные частоты (F_j).

В. Вычислить скорректированные накопленные частоты (F*_j) по приведенной ниже формуле:

F*_j = F_j – 0,5 f_j.

Г. Вычислить процентильные ранги по следующей формуле:

PR_j = F_j × 100/ n,

где PR_j – процентильные ранги,

F_j – накопленная частота,

n – число испытуемых.

Д. По таблице функции нормального распределения
(см. приложение 1) определить значения s, соответствующие вычисленным процентильным рангам.

Е. Выразить полученные результаты в стандартной шкале стенайнов, воспользовавшись следующей формулой:

z_j = 2×s_j + 5.

2. Произвести линейную стандартизацию суммарных баллов по таблице 19.

А. Вычислить среднее арифметическое по «сырым» баллам :

;

= (4 ×2 + 5×2 + 6×5 +7 ×8 +8×14 +9 ×9 +10 ×6 +11 ×3+12 ×1) / 50 = = 402 / 50 = 8,04.

Б. Найти разности x _i – и их квадраты – (x _i – )².

В. Вычислить стандартное отклонение по формуле:

;

S_x = [(16 ×2+9 ×2+4 ×5+1 ×8+0 ×14+1 ×9+4 ×6+9 ×3+16 ×1) / (50-1)]^1/2 = = (154/49)^1/2 = 3,14^1/2 = 1,77.

Г. Перевести «сырые» баллы в стандартную шкалу стеанайнов по формуле:

.

Д. Округлить полученные значения z_j и z′_j и вписать в таблицу (см. табл. 19).

 

Таблица 19

Линейная стандартизация шкалы

 

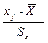
Экстра-версия Xj	хj –	(хj – )2		z′j	Округленные значения
zj	z'j
	-4		-2,26	0,48
	-3		-1,69	2,62
	-2		-1,13	2,74
	-1		-0,85	3,3
			0,85	6,7
			1,13	7,26
			1,69	8,38
			2,26	9,52

 

Анализ результатов и выводы

Сравнить значения z_j и z′_j.

В нашем примере в 5 парах значения z_j и z′_j не совпадают друг с другом.

Сделать вывод о нормальности распределения частот суммарных баллов и репрезентативности выборки. Если сравниваемые пары значений совпадают, то делается вывод о нормальности эмпирического распределения и репрезентативности выборки. В нашем случае выводы состоят в следующем.

1. Распределение частот суммарных баллов отличается от нормального.

2. Выборка испытуемых нерепрезентативна по отношению к генеральной совокупности.

 

 

Лабораторная работа № 12

Проверка устойчивости распределения

С помощью критерия хи-квадрат

Вводные замечания. Традиционный способ доказательства устойчивости сводится к выяснению степени приближения эмпирического распределения к какому-либо теоретическому. Если эмпирическое распределение не приближается к теоретическому, несмотря на значительное увеличение численности выборки, то приходится прибегать к более общему индуктивному методу доказательства.

Цель: определить устойчивость распределения тестовых оценок первичной формы опросника сравнением эмпирического и теоретического распределений.

Материал: оцениваемый тест, таблица по математической статистике, результаты тестирования испытуемых по проверяемому опроснику, калькулятор.

 

Ход работы

1. Случайным образом составить выборку стандартизации.

2. Провести обследование испытуемых с помощью оцениваемого теста.

3. Полученные результаты внести в таблицу для вычисления теоретических частот (см. табл. 20).

Таблица 20

Расчет теоретических частот, соответствующих

Нормальному распределению первичных тестовых оценок

Оценка теста	Эмпирическая частота (р)	хi –	(хi – )2		f (z)	Теоретическая частота
		-5,4	29,16	-1,93	0,06195	1,327
		-4,4	19,36	-1,62	0,01741	2,302
		-3,4	11,56	-1,19	0,19652	4,21
		-2,4	5,76	-0,85	0,27798	5,96
		-1,4	1,96	-0,51	0,35029	7,506
		-0,4	0,16	-0,14	0,39505	8,465
		0,6	0,36	0,21	0,38761	8,306
		1,6	8,56	0,58	0,33718	7,225
		2,6	6,76	0,9	0,26129	5,6
		3,6	12,96	1,33	0,16474	3,53
		4,6	21,16	1,61	0,10915	2,339
		5,6	31,36		0,05399	1,157
∑			149,12

 

А. Вычислить среднее арифметическое по формуле:

.

Б. Вычислить для каждого х_i разность х_i – и полученные значения возвести в квадрат.

В. Вычислить среднее квадратичное отклонение S_x

.

Г. Вычислить .

Д. Найти по таблице значения ординаты нормальной кривой f (z)(см. приложение 2).

Е. Вычислить теоретические частоты по формуле:

_.

Полученные результаты внести в таблицу (см. табл. 20).

4. Оценить расхождение между теоретическим и эмпирическим распределением частот, используя для расчетов данные таблицы 20. Пример расчета показан в таблице 21.

 

Таблица 21

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: