Расчет силы отдельных пунктов опросника

 

№ испытуемых п/п	Номера пунктов и ответы на них
			…
	+	+	-		-
	-	+	-		-
	+	-	-		+
	+	+	+		+
	+	+	-		+
	+	+	+		+
	+	+	-		+
	-	-	+		+
	+	-	-		-
	-	+	+		+
	+	+	-		+
	-	+	+		+
	+	-	+		+
	-	+	-		-
	+	+	-		+
	-	-	+		+
	+	-	-		-
	-	+	-		-
	+	+	+		+
	+	+	-		-
	-	-	+		+
	+	+	-		+
	+	-	-		-
	-	-	-		-
	+	+	-		-
Кол-во ответов «да»
Сила пункта
Очень сильные
Очень слабые
Оптимальные	+	+	+		+

 

4. Оценить статистическую значимость различий пунктов по силе, используя таблицу критических значений критерия χ² (см. приложение 3) для α = 0,05 и числа степеней свободы υ = 2.

Сравнить эмпирическое и критическое значения c². Если эмпирическое значение меньше критического, то различия не значимы, случайны. Если эмпирическое значение больше критического, то различия значимы, то есть пункты существенно отличаются друг от друга по силе.

Анализ результатов и выводы

1. Выявить чрезмерно сильные пункты, то есть те, которые содержат утверждения, с которыми большинство испытуемых не может согласиться. К ним относятся утверждения, сила которых меньше 25 %.

2. Выявить чрезмерно слабые пункты, то есть те, которые содержат утверждения, индекс силы которых больше 75 % и большинство испытуемых вынуждено согласиться с их содержанием.

3. Отметить те пункты, которые являются оптимальными по силе. Это пункты, индекс силы которых равен 25-75 %.

4. Вычислить среднее значение индекса силы у пунктов, признанных оптимальными по силе.

5. Сделать вывод о сбалансированности пунктов опросника по силе. Опросник считается сбалансированным по силе, если среднее значение индекса силы по всем ее пунктам приблизительно равно 50 %. В ином случае необходимо удалить либо более сильные, либо более слабые пункты.

Сделать вывод о дальнейшей судьбе каждого пункта. При использовании дихотомической шкалы ответов (ответы «да» или «нет»), чрезмерно сильные или чрезмерно слабые пункты требуют корректировки или должны быть удалены из опросника.

 

 

Лабораторная работа № 5

Расчет коэффициента дискриминативности

 

Вводные замечания. Коэффициент дискриминативности (или согласованности) отдельной задачи с тестом – второй статистический показатель, позволяющий оценить, насколько точно задача дифференцирует испытуемых по измеряемому признаку. Он равен коэффициенту корреляции между средним результатом анализируемой задачи (по принципу правильный – неправильный ответ) и средним первичным результатом по всем задачам теста. Для расчета коэффициента дискриминативности применяют коэффициент точечно-бисериальной корреляции.

Цель: усвоить процедурувычисления коэффициента дискриминативности на примере одного пункта оцениваемого опросника.

Материал: результаты тестирования испытуемых с помощью оцениваемого теста, калькулятор.

Ход работы

 

1. Обследовать группу испытуемых с помощью оцениваемого опросника.

2. Полученные результаты внести в общую таблицу, в которой указываются ответы испытуемых на каждый пункт и суммарный балл по тесту (см. табл. 10).

 

Таблица 10

Результаты обследования испытуемых
с помощью первичной формы опросника

 

№ испытуемого п/п	№ пунктов и ответы на них	Суммарный балл
		…
	+	+		+	-
	-	+		+	-
	+	-		-	+
	+	+		+	+
	+	+		+	+
	+	+		+	+
	+	+		-	+
…
	+	+		-	-
Сумма ответов «да»

 

3. В таблице 10 представлены результаты тестирования по 12 пунктам опросника. Все пункты предполагают ответ «да» или «нет», при совпадении которого с ключом испытуемому присваивается один балл. Поскольку расчет коэффициента дискриминативности – довольно трудоемкий процесс, предлагаем вычислить его только для одного пункта (в нашем примере для одиннадцатого пункта). Для расчета коэффициента дискриминативности следует заполнить следующую таблицу (см. табл. 11).

 

Таблица 11

Расчет коэффициента дискриминативности
для одиннадцатого пункта теста

 

хi	f	f∙x	f∙x 2	f п11	f п11 ∙x
	N = 25	∑ х = 163	∑ х 2 = 1121	N п11 = 10	∑ х п11 = 77

 

Примечание:

х_i – первичный результат, полученный испытуемым по тесту;

f – количество, испытуемых получивших результат х_i;

f_{п 11} – количество испытуемых, получивших результат х_i и ответивших «да» на одиннадцатый пункт (ответ «да» в данном случае означает совпадение с ключом). Эти данные содержатся в таблице 10.

 

4. Подставить полученные в последней строке таблицы значения в формулу для расчета коэффициента дискриминативности. Он рассчитывается по формуле точечно-бисериального коэффициента корреляции:

_.

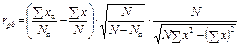5. Сравнить полученный результат с силой данного пункта и сделать выводы.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: