 |
Динамические режимы работы ТТГГ
|
|
|
|
Для исследования динамических режимов процессов горения уравнение Бори дополняется уравнением состояния газа в виде уравнения Менделеева-Клайперона – изменение давления от изменения массы в объёме камеры сгорания:
где:
V - объём камеры сгорания ТГ,
m - масса газа в пределах свободного объёма камеры сгорания,
R - универсальная газовая постоянная [ кГ∙см/(кг∙°К) ],
Т - температура газа [ °К ].
Дифференцируя уравнение состояния по частям (правое и левое выражения), получаем:
Так как процесс изменения объёма камеры сгорания линейно зависит от скорости горения
то, подставляя в дифференциальное уравнение газового баланса, получим:
Уравнение нелинейно, решение находится методом Лагранжа при замене переменной Рn =z [2] или с использованием программного продукта Simulink MatLab.
Для анализа динамического состояния протекания внутрикамерных процессов в ТГ достаточно эффективна линеаризованная модель, которая позволяет, используя преобразование Лапласа, строить переходные процессы изменения давления в камере сгорания от действия возмущающих факторов, наиболее часто встречающихся в практике проектирования зарядов ТГ и отработки конструкции.
Остановимся на двух, наиболее часто встречающихся возмущениях: изменение площади проходного сечения сопла и изменение поверхности горения топлива.
2.3.1. РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА В ТГ НА ИЗМЕНЕНИЕ ПЛОЩАДИ ПРОХОДНОГО СЕЧЕНИЯ СОПЛА
Исходные данные:
1. Давление в камере ТГ Р [ 
]
2. Массовый секундный расход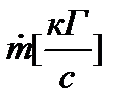 
3. Закон горения топлива
где:
u1 =0,011 - коэффициент чувствительности скорости горения к температуре,
ν =0,62 - показатель степени в законе горения.
|
|
|
4. Начальный объём Vо [cм3].
5. Универсальная газовая постоянная R=4000
| К |
| кГ |
| см |
| кг |
| × |
| × |
6. Температура газа T=1200 ºК.
7. Время действия возмущения τ [с].
8. Изменение критического сечения Ds [cм2].
9. Удельный вес g= 1,55∙10-3 [кГ/см3].
Методические указания.
1.Дифференциальное уравнение, описывающее работу ТГ на основании уравнения сохранения массы, имеет вид:
где:
V=Vo+u1·Pν·τ·S - текущее значение объёма.
k =1,25 - коэффициент изоэнтропы.
3. Процедура линеаризации уравнения 1) в приращениях ∆Р и ∆σ относительно «замороженных» значений Р0 и s0 приводит его к виду:
С учётом того, что ΔР·Δσ ~0 и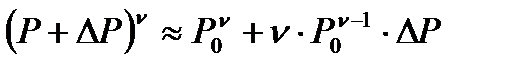 
,
получим:
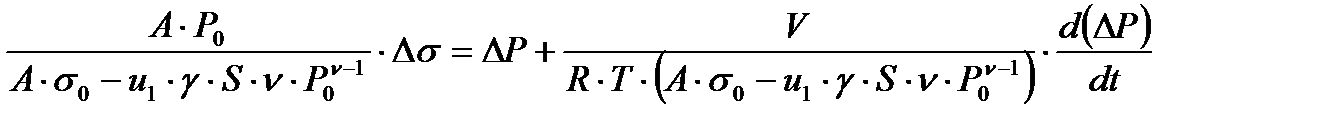
или с учётом обозначения 
- оператором дифференцирования (Лапласа), опустив приращение 
, получим:
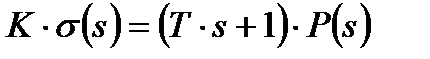
где:
4. Передаточная функция ТГ при изменении критического сечения:
является апериодическим звеном первого порядка с переходной функцией, полученной на ступенчатое изменение проходного сечения в виде:
График переходного процесса Р(t) на ступенчатое уменьшение критического сечения представлен на рис. 2.5
| -Ds |
| РК0 |
| s0 |
| t |
Рис. 2.5. Переходный процесс Р=f(t) на ступенчатое изменение σ
Примечание. Определение стационарного значения проходного сечения сопла производят из уравнения Бори для стационарного режима работы ТГ:
После определения численных значений параметров дифференциальных уравнений составляют математическую модель решения линейной и нелиненой задач: определение реакции давления на ступенчатое изменение площади проходного сечения сопла, структура которой представлена на рис. 2.6.
Структура составлена таким образом, чтобы можно было сравнить результаты решений линейной и нелиненой задач на участке переходного процесса и тем самым определить динамическую и статическую ошибки решений (рис.2.7).
|
|
|
Рис. 2.6. Структурная схема линейной и нелиненейной моделей ТГ
Рис. 2.7. Переходный процесс изменения Р=f(t) на ступенчатое
уменьшение проходного сечения сопла и ошибка ∆Р=Рл-Рн
линейной по отношению к нелинейной задаче
2.3.2. РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА В ТГ НА ИЗМЕНЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ ГОРЕНИЯ
Исходные данные:
1. Давление в камере ТГ Р [кГ/см2]
2. Массовый расход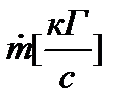
3. Закон горения топлива
где:
u1 =0,01 - коэффициент чувствительности скорости горения к температуре,
ν =0,62 - показатель степени в законе горения.
4. Начальный объём V [cм3].
5. Универсальная газовая постоянная R=4000 [кг∙cм/(кГ·ºК)].
6. Температура газа T=1200 ºK.
7. Время действия возмущения τ [с].
8. Возмущение ΔS.
9. Удельный вес топлива g=1,55∙10-3 [кГ/см3].
Методические указания.
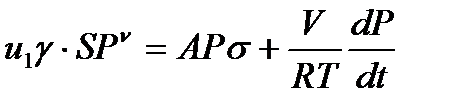
1.Дифференциальное уравнение работы ТГ на основании уравнения сохранения массы
где:
V=Vo+u1PντS - текущее значение объёма.
k =1,25 - коэффициент изоэнтропы.
2.Линеаризация уравнения (1):
С учётом:
ΔР·ΔS ~0,
получим:
или с учётом обозначения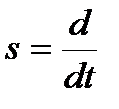 
- оператором дифференцирования:
где:
3. Передаточная функция ТГ при изменении поверхности горения:
является апериодическим звеном первого порядка с переходной функцией на ступенчатое изменение поверхности горения в виде соотношения:
график которого представлен на рис. 2.8
| +DS |
| РК0 |
| S0 |
| t |
Рис. 2.8. Переходный процесс Р=f(t) на ступенчатое изменение S
Примечание:
Оценку стационарного значения поверхности горения следует производить при использовании уравнения Бори:
После определения численных значений параметров дифференциальных уравнений составляют математическую модель решения линейной и нелиненой задач: определение реакции давления на ступенчатое изменение площади проходного сечения сопла, структура которой представлена на рис. 2.9.
Структура составлена таким образом, чтобы можно было сравнить результаты решений линейной и нелиненой задач на участке переходного процесса и тем самым определить динамическую и статическую ошибки решений рис.2.10.
Рис. 2.9. Структурная схема линейной и нелиненейной моделей ТТГГ
|
|
|
Рис. 2.10. Переходный процесс изменения Р=f(t) на ступенчатое
увеличение поверхности горения S для линейной и нелинейной задач
Возмущающее воздействие в виде изменения поверхности горения DS(t) характерно для случая программной смены режима работы ТГ. Как правило, для экономии массы ТГ свод заряда профилируют или изменяют величину проходного критического сопла в соответствии с участками работы возмущённого движения ЛА, полученными в результате моделирования. При этом статистический анализ возмущённых траекторий показывает, что наиболее напряжёнными являются участки:
1) Разделения ступеней,
2) Действие в процессе полёта специальных факторов ПФЯВ.
S
2)
1)
t
Знание динамики горения топлива при переходе с режима на режим расширяет область применения ТТГГ с различными потребителями газовой энергии.
Возмущение в виде изменения площади критического сечения сопла характерно при длительном времени работы ТГ к моменту окончания работы, когда происходит или зашлаковка сопла или разгар сопла.
Следует отметить, что переходные процессы изменения давления в камере сгорания на возмущения в виде изменения поверхности или критического сечения могут быть идентичны, что затрудняет анализ аномалий в ТТГГ в процессе эксплуатации.
Применяемые в настоящее время методы определения зашлаковки сопел сводятся к замерам фактических размеров сопла до и после испытаний и к анализу характера зависимости Р(t). Однако эта процедура не даёт истинной картины состояния сопла во время работы, поскольку подъём и последующие спады давления могут происходить как из-за зашлаковки сопла, так и из-за аномальной работы порохового заряда (длительное или кратковременное изменение поверхности горения). Сравнение диаметра критического сечения сопла до и после испытаний не позволяет определить действительную причину аномальной работы, так как сопло, работавшее основное время без изменения своего состояния, может подвергнуться интенсивной зашлаковки по окончании работы ТГ при спаде давления и догорании остатков топлива, когда в продуктах сгорания из-за низкой температуры газа содержание К -фазы повышено.
|
|
|
В основу метода идентификации возмущений положено сравнение переходных процессов, протекающих в ресивере – камере-анализаторе переходных процессов при действии двух основных видов возмущения: изменение критического сечения сопла (изменения оборотов газового мотора или проходного сечения регулятора давления в ВА) и изменения величины поверхности горения.
РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА В РЕСИВЕРЕ ТГ (Рис. 2.11) НА ВОЗМУЩАЮЩЕЕ ВОЗДЕЙСТВИЕ В КАМЕРЕ СГОРАНИЯ-РИЗМЕНЕНИЕ КРИТИЧЕСКОГО СЕЧЕНИЯ СОПЛА КАМЕРЫ СГОРАНИЯ (ИМИТАЦИЯ ЗАШЛАКОВКИ ПРОДУКТАМИ СГОРАНИЯ)
| Р Рр |
| фильтр |
| Эталонное сопло |
| Испытуемое сопло |
Рис. 2.11. Расчётная схема ТГ с ресивером
Исходные данные:
1. Давление в камере ТГ Р [ кГ/см2]
2. Массовый расход 
[кГ/с]
3. Закон горения топлива
где:
u1 =0,01 - коэффициент чувствительности скорости горения к температуре,
ν =0,62 - показатель степени в законе горения.
4. Начальный объём камеры сгорания Vо [cм3].
5. Универсальная газовая постоянная R=4000 [кгсм/(кГ·ºК)].
6. Температура газа T=1200 ºK.
7. Время действия возмущения τ [с].
8. Объём ресивера Vр [cм3].
9. Проходное сечение сопла ресивера σр=2σо [cм2].
10. Изменение проходного сечения сопла Δσo=0,1σо
11. Удельный вес g=1,55∙10-3 [кГ/см3].
Методические указания.
1.Дифференциальные уравнения изменения процессов горения топлива в камере сгорания топлива в ТГ и камере ресивера на основании уравнения сохранения массы имеет вид
где:
V=Vo+u1PντS - текущее значение объёма.
Рр - давление в ресивере.
k =1,25 - коэффициент изоэнтропы.
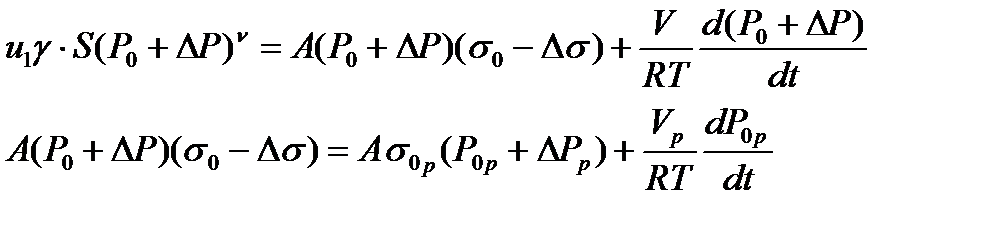
2.Линеаризуя уравнения (1):
с учётом:
ΔР·Δσ ~0,
получим:
или с учётом обозначения 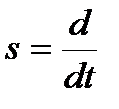- оператором дифференцирования (Лапласа):
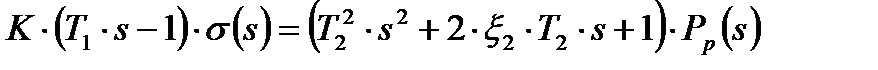
где:
4. Передаточная функция ТГ при изменении критического сечения:
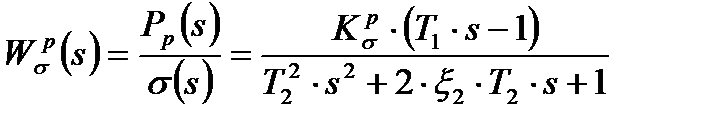
представляется неминимально-фазовым колебательным звеном с переходной функцией на ступенчатое изменение проходного сечения в виде:
где 
Примечание. Определение стационарного значения проходного сечения сопла и стационарного давления в ресивере при отсутствии возмущения находят в результате решения уравнения Бори для стационарного режима работы ТГ:
Графики переходных процессов представлены на рис. 2.12
| РК |
| Р Р |
| РР0 |
| РК0 |
| s0 |
| -Ds |
| t |
Рис. 2.12. Переходные процессы изменения Рк, Рр=f(t) при
ступенчатом изменении σ
Как следует из графиков переходных функций изменения давления в камере сгорания и в ресивере, качественная картина их имеет существенное различие. При скачкообразном уменьшении величины критического сечения увеличение давления в камере сгорания носит экспоненциальный характер, в то время как реакция давления в ресивере имеет на момент действия возмущения характерный провал с последующим экспоненциальным ростом. Такая картина свойственна реакции устойчивого неминимально-фазового звена на скачок возмущения. Физически провал давления образуется из-за инерционности процесса роста скорости горения на первоначальное уменьшение критического сечения при последующем увеличении газоприхода и перехода давления на новый повышенный стационарный уровень.
|
|
|
После определения численных значений параметров дифференциальных уравнений составляют математическую модель решения линейной и нелиненой задач: определение реакции давления на ступенчатое изменение площади проходного сечения сопла, структура которой представлена на рис. 2.13.
Структура составлена таким образом, чтобы можно было сравнить результаты решений линейной и нелиненой задач на участке переходного процесса и тем самым определить динамическую и статическую ошибки решений рис.2.14.
Рис. 2.13. Структурная схема линейной и нелинейной моделей
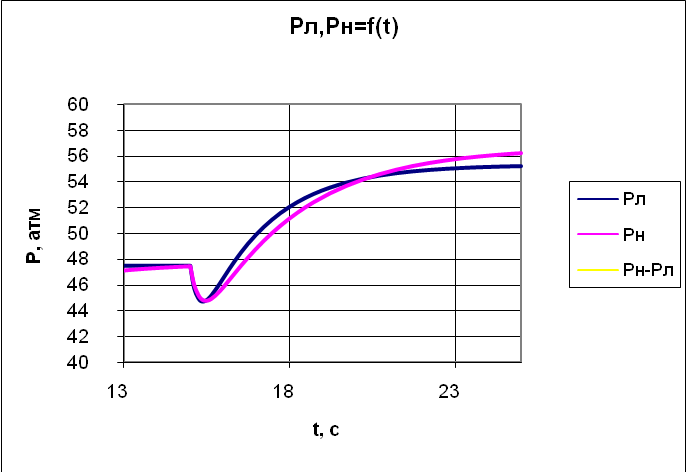
Рис. 2.14. Переходный процесс изменения давления в ресивере на
|
|
|
