Расчёт индикаторной диаграммы – характеристики эффективности газового мотора
Энергетические показатели газового мотора, его рабочий цикл характеризуются индикаторной диаграммой каждого поршня, который производит работу за счёт расширения подпоршневого объёма. Индикаторная диаграмма строится в плоскости «давление – объём». Степень совершенства рабочего цикла оценивается полнотой индикаторной диаграммы, другими словами, интегралом (площадью) под кривой давления, а также, минимизацией потерь механической энергии в процессе впуска газа в полость силового цилиндра. Чем больше площадь, ограниченной кривой Р=f(V), тем большую работу совершает поршень.
В работе [5] показано, что оптимальным для режима работы газового двигателя в диапазоне частот вращения 6000…10000 об/мин является круглое отверстие впуска с диаметром ~ 4,5 мм.
При составлении расчётной методики получения индикаторной диаграммы использованы методы расчёта динамики глухих камер для турбулентных и ламинарных дросселей [6]. Все рассуждения проводятся при двух общих допущениях.
1. Неустановившиеся процессы течения газа через переменный дроссель рассматриваются как квазистатические, т. е. принимается, что в переходном процессе в каждый момент времени мгновенное значение расхода газа через дроссель такое же, каким оно было бы при данной разнице давлений в условиях установившегося течения; действие сил инерции, неучтённое при введении этого допущения, приводит к запаздываниям, характеризуемых постоянными времени, обычно несоизмеримо малыми в сравнении с постоянными времени, обусловленными ёмкостью камер.
2. Предполагается, что изменение состояния газа в полости блока цилиндров подчинено адиабатическому закону; в действительности при переходных процессах чаще всего состояние некоторой массы газа в полости не следует закону адиабаты, и обычно для камер рассматриваемых типов процессы изменения состояния являются промежуточными между адиабатическими и изотермическими процессами. Однако разница между временами заполнения и опорожнения полостей при изотермическом и адиабатическом изменениях состояния газа в полости невелика.
При получении выражений для построения индикаторной диаграммы ГМ следует различать полости с дросселями турбулентными (истечение газа через переменное отверстие блока цилиндров) и ламинарными (истечение газа через кольцевой зазор между плунжером и блоком цилиндров).
Алгоритм расчёта охватывает три цикла индикаторной диаграммы:
1. Цикл заполнения полости через дроссель переменного сечения при переменном расширении объёма.
2. Цикл расширения объёма и опорожнения газа через торцовый и кольцевой зазор.
3. Цикл опорожнения газа через переменное выхлопное отверстие.
РАБОЧИЙ ЦИКЛ ВПУСКА ГАЗА В ПЕРЕМЕННЫЙ ОБЪЁМ ЧЕРЕЗ ПЕРЕМЕННОЕ СЕЧЕНИЕ ВПУСКНОГО ОТВЕРСТИЯ
Для получения характеристик заполнения и опорожнения будем пользоваться расчётной схемой, представленной на рис. 2.27
f(w· t)
Р к, V(w· t)
Р1
V
Vo
aотс aвых wt
+
+
+ a= wt
Рис. 2.27. Расчётная схема цикла впуск газа
Считая, что заполнение полости цилиндра происходит при Р1=const (игнорируются высокочастотные пульсации с малой амплитудой), и учитывая, что температура газа Т=const, получим из характеристического уравнения выражение для изменения параметров в полости:
Выражение для изменения массы газа в полости имеет вид:
из которого следует зависимость для массового cекундного расхода газа:
С другой стороны, в соответствии с формулой для массового прихода газа через проходное сечение f(w∙t) в поршневую полость переменного объёма блока цилиндров газового мотора имеем:
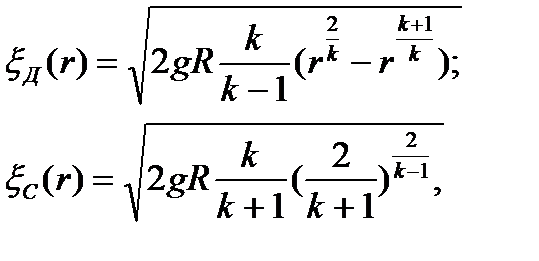
где для докритического и сверхкритического характера истечений значения комплекс x(r) записывают в следующем виде:
где:
r=PК/Р1 – относительное давление в полости цилиндра; Р1=Const – давление газа на входе в газовый мотор, k – показатель адиабаты; R – газовая постоянная; V(ωt) – величина текущего значения объём полости блока цилиндров; f(ωt) – величина текущего значения площади проходного сечения для газа; e - коэффициент расхода газа; Т – абсолютная температура.
Приравняв правые части выражений для массового секундного расхода и прихода газа  и разделив переменные r и t, получаем:
и разделив переменные r и t, получаем:
Считаем с погрешностью < 5…7%, что f(ωt)=kf ∙ w∙t,

где:
n – частота вращения вала в минуту газового мотора,
fmax – максимальная площадь отверстия в блоке цилиндров,
Da - угловой размер (растр) отверстия в блоке цилиндров для впуска газа в полость,
Vo – “начальный” объём полости ГМ,
Vmax – максимальный объём, образуемый при движении поршня,
dц – диаметр поршня,
Dб – диаметр делительной окружности расположения поршней блока цилиндров,
g - угол наклона оси выходного вала ГМ к оси вращения блока цилиндров.

Для wt=52° < 60°: Coswt ~1-(w∙t)2/2. Подставив f(ωt)=kf∙w∙t и V(ωt) в последнее равенство, получим:
где:


Подставив функцию xс(r) для сверхкритического истечения газа в полость ГМ и выполнив интегрирование левой и правой частей дифференциального уравнения в пределах 0…t и ro…rкр, получим:
где:
- 
относительное начальное давление в полости цилиндра, равное относительному давлению выхлопа газа,
rкр – относительное критическое давление в полости цилиндра.
Интегрируя правую и левую части, получим:
Преобразование полученного соотношения позволяет получить зависимость давления в полости блока цилиндров от времени t (или угла  ) для сверхкритического истечения газа в полость в виде:
) для сверхкритического истечения газа в полость в виде:

Для определения времени заполнения полости при сверхкритическом истечении следует в tзc подставить относительный критический перепад давления

Для нахождения зависимости давления от времени при докритическом перепаде между входным давлением и относительном критическом перепаде давления необходимо комплекс xД(r) подставить в исходное выражении. В результате имеем:

После интегрирования получаем:


откуда:

Подстановка r=1, при котором уравниваются давления на входе и в полости газового мотора, и прекращается заполнение полости, получаем время заполнения полости при докритическом перепаде давления.

Полное, суммарное время заполнение полости ГМ находят сложением соответствующих времён при сверхкритическом и докритическом перепадах давления:
Воспользуйтесь поиском по сайту:


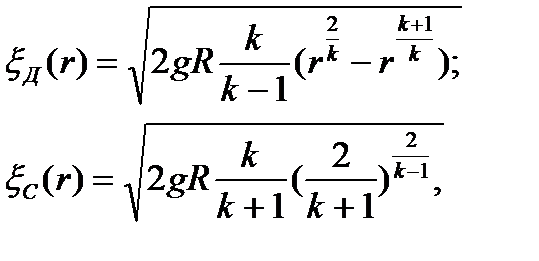
 и разделив переменные r и t, получаем:
и разделив переменные r и t, получаем:




 ) для сверхкритического истечения газа в полость в виде:
) для сверхкритического истечения газа в полость в виде:








