Рабочий цикл расширения газа в переменном

ОБЪЁМЕ ПОЛОСТИ БЛОКА ЦИЛИНДРОВ

 

Цикл опорожнения полости газового мотора после отсечки от отверстия впуска до подхода блока цилиндров к отверстию выхлопа происходит через кольцевой зазор, образуемый между полостью и двигающимся поршнем (рис.2.28), при увеличивающемся, по мере поворота ГМ, объёме полости.

 

α=ωt

 

 

 

 

 

Рис.2.28. Расчётная схема цикла расширения

Для полости с движущимся поршнем дифференциальное уравнение имеет вид:

,

)

(

к

к

f∙Р

dt

dP

RT

t

V

-

=

w

где:

p

d

m

ц

f

d

lRT

=

-

f - проводимость кольцевого зазора; d_ц – диаметр поршня; d - кольцевой зазор в плунжерной паре, m =(374+5,03Т)10^-12 Н∙с/см² – динамическая вязкость газа; l – длина плунжера.

ú

û

ù

ê

ë

é

-

÷

÷

ø

ö

ç

ç

è

æ

+

=

-

+

=

t

Cos

k

V

k

t

Cos

k

V

t

V

V

o

V

V

o

w

w

w

)

(

)

(

 

 

 

Разделив переменные, произведём интегрирование в пределах Р_t…P_к:

 

где Р_t – текущее значение давления (Р_t<Р_к) или в безразмерном виде r= Р_t/Р_к.

Обозначив V_o/k_V+1=a>1, получим:

 

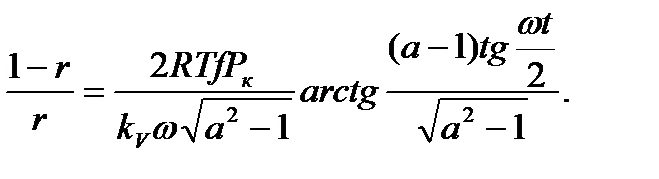
Откуда выражение для определения времени (или угла), при котором происходит работа расширения в полости блока цилиндров, для случая истечения газа через ламинарный дроссель (кольцевой зазор) имеет вид:

 

Так как w∙t=a - угол поворота блока цилиндров относительно распределителя газа является геометрическим параметром, то подставив a=ω∙t_ОП=2π, можно определить давление газа в полости ГМ к моменту выхлопа.

 

РАБОЧИЙ ЦИКЛ НА ВЫХЛОПЕ ИЗ ГАЗОВОГО МОТОРА

 

После окончания цикла расширения газа при его истечении через зазор наступает цикл выхлопа газа из полости в выхлопную магистраль (рис. 2.29).

 

 

α=ωt

 

 

Рис. 2.29. Расчётная схема цикла выхлопа газа.

Так как угол, при котором опорожняется полость, мал (a=wt <14°), то V(ωt)=Const и Coswt=0, а объём полости достигает максимальное значение и вычисляется по соотношению:

 

Полагая r=P_вых/Р_к, Р_вых=Const, имеем

Подставляя последнее равенство в характеристическое уравнение d =(V/RT)dP_к, записываем следующее дифференциальное уравнение, описывающее процесс изменения давления в цикле выхлопа газа из ГМ:

 

 

Уравнение истечения газа из полости газового мотора

),

(

)

(

к

r

T

R

P

t

f

m

dt

dm

x

w

e

=

=

&

имеет вид:

 

 

)

(

)

(

r

r

dr

V

t

f

T

x

w

e

-

=

Для сверхкритического перепада давления, когда r_кр<0,5, преобразованное дифференциальное уравнение имеет вид:

 

В пределах интегрирования t=0…t, r=1…r_кр время опорожнения вычисляется по выражению:

 

 

Для докритического перепада давления между полостью и магистралью выхлопа, когда r_кр>0,5, дифференциальное уравнение имеет вид:

 

Интегрирование правой части для произвольных «k» не производится. Произведём эту операцию для горячего газа k=1,25 и воздуха k=1,4.

Для горячего газа в пределах интегрирования 0…t и r_кр…r_o=1 время опорожнения определяется по выражению:

где Ф(r_кр) определяется в результате подстановки r_кр в Ф(r).

Для воздуха в пределах интегрирования 0…t и r_кр…r_o=1 время опорожнения определяется по выражению:

 

 

где:

Время полного опорожнения полости определяется равенством:

.

 

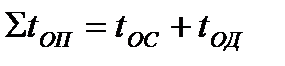Построение индикаторной диаграммы давления в полости блока цилиндров состоит в припасовке соответствующих циклов диаграммы. Качественнная картина индикаторной диаграммы представлена на рис. 2.30.

 

 

P

 

 

 

 

V

 

Рис. 2.30. Индикаторная диаграмма газового мотора:

- реальная диаграмма,

- идеальная диаграмма.

Разница в площадях идеальной S_и и реальной S_p диаграмм свидетельствует об эффективности, совершенстве газового цикла в газовом моторе. Объёмный КПД определяется по соотношению

 

 

Для разработанного ряда газовых моторов объёмный КПД составляет K_Q=0,7…0,8.

ОЦЕНКА ВЛИЯНИЯ ПУЛЬСАЦИЙ ДАВЛЕНИЯ В

СИСТЕМЕ ТГ-ГМ

Совместная работа ТГ и ГМ характеризуется наличием пульсаций давления на входе в газовый мотор, появляющихся в результате отсечки отверстия впуска, через которое происходит течения газа в полости ГМ от ТГ.

Считая, что основная часть газоприхода идёт на заполнение полости поршня (только 20…25% затрачивается на компенсацию непроизводительных утечек) целесообразно рассмотреть влияние пульсаций давления в полости ГМ на работу ТГ.

Частота появления в просвете газовода переменных объёмов полостей цилиндров, а, следовательно, частота изменения расхода обусловлена скоростью вращения блока цилиндров в соответствии с механической характеристикой энергоблока ТГ-ГМ и может быть рассчитана по соотношению

 

где:

z – количество поршней блока цилиндров;

w - угловая скорость вращения блока цилиндров.

Для наглядности представления методики оценки пульсаций целесообразно использовать расчётную схему, представленную на рис. 2.31:

Р1

Р2

 

w

 

Рис. 2.31. Расчётная схема пульсаций давления:

1 -ТГ; 2 -фильтр; 3 -газовод: 4 -ГМ

 

При выводе уравнений приняты следующие допущения:

- продукты сгорания твёрдого топлива подчиняются уравнению состояния для идеального газа;

- температура газа и перепад давления на фильтре постоянны.

Уравнение сохранения массы для камеры сгорания 1 заряда имеет вид:

 

 

где V - свободный объём камеры сгорания заряда, Р₁ -давление газа в камере сгорания, _рас - массовый секундный расход газа.

Расход газа через фильтр 2 при докритическом перепаде давления между камерой сгорания 1 и газоводом 3 (Р₂/Р₁>0,5) определяется выражением:

 

 

где s₁ -площадь эффективного сечения, которое представляет собой фильтр, обеспечивающий перепад давления DР= Р₂ - Р₁, давление Р₂ -давление в газоводе.

После подстановки, уравнение состояния будет иметь вид:

 

 

Дифференциальное уравнение нелинейно. Проведение линеаризации правой части в окрестности установившихся параметров Р₁₀, Р₂₀ разложением в ряд Тейлора и отбрасывание членов второго порядка малости даёт погрешность результата динамики процессов не превышающей 10…12%.

Линеаризация первого члена правой части приводит к результату в виде:

 

Линеаризацию второго члена следует провести по двум переменным Р₁ и Р₂, при этом:

где:

Подставив линеаризованные члены уравнения в уравнение расхода, получим линейное дифференциальное уравнение первого порядка для оценки давления в камере сгорания:

Используя преобразование Лапласа, получим передаточную функцию, как реакцию давления в камере сгорания на изменение давления в газоводе:

 

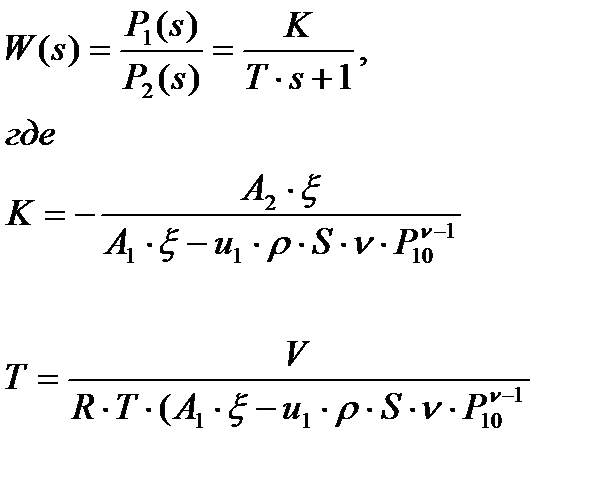
Для апериодического звена первого порядка амплитудно-частотная записывается в виде:

 

График АЧХ представлен на рис. 2.32 для следующих параметров: k=1,25; n=0,5; u₁=0,03; r=1,55*10^-3 кГ/см³; S=35,7 cм²; Р₁₀=6 Мпа; Р₂₀=5,5 МПа; s₁=0,232 см²; R=4000 кГсм/(кг·°К); Т=1400 °К; V=500 cм³; А₁·ξ=-0,62; А₂·ξ =-0,467.

А(w)

 

1,0

0,75

0,5

0,25

w [рад/с]

0 25 50 75 100

 

Рис. 2.32. АЧХ ТГ при изменении частоты давления Р₂

 

Из графика следует, что амплитуда колебаний давления в камере ТГ при возмущении в газоводе колебаний давления на частотах w близких к 0 составляет 0,77 изменения в газоводе. При увеличении частоты колебаний в газоводе в диапазоне 5…50 рад/с отмечено падение коэффициента передачи колебаний до ~ 15%, а при рабочих частотах >100 рад/с ослабление амплитуды становится пренебрежимо мало.

 

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: