 |
Формулы, описывающие ограничения модели
|
|
|
|
| Левая часть ограничения | Формула Excel |
| =СУММПРОИЗВ(B$3:D$3;B13:D13) |
| =СУММПРОИЗВ(B$3:D$3;B14:D14) |
| =СУММПРОИЗВ(B$3:D$3;B15:D15) |
| =СУММПРОИЗВ(B$3:D$3;B16:D16) |
| =СУММПРОИЗВ(B$3:D$3;B17:D17) |
Напоминаем, что ввод соответствующей формулы в каждую ячейку необязателен, достаточно в ячейку E13 внести формулу =СУММПРОИЗВ(B$3:D$3;B13:D13), а потом воспользоваться возможностью автозаполнения формул в других ячейках.
В экранной форме (Рис. 3) в ячейках E13, E14, E15, E16, E17 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рис. 3. Окно после ввода зависимостей в математической модели
4. Установите целевую ячейку и укажите направление поиска, для этого:
· зайдите в меню Сервис à Поиск решения;
· в поле «Установить целевую ячейку» укажите целевую ячейку $B$9;
· введите направление оптимизации ЦФ, щелкнув один раз левой клавишей мыши по кнопке «минимальному значению»;
5. Укажите диапазон изменения ячеек, для этого в окне «Поиск решения» в поле «Изменяя ячейки» впишите адреса $B$3:$D$3.
Напоминаем, что необходимые адреса можно вносить в поле автоматически, путем выделения мышью соответствующих ячеек переменных непосредственно в экранной форме.
6. Внесите условие неотрицательности для переменных (в окне «Поиск решения») (Рис. 4), для этого:
· нажмите кнопку «Добавить», после чего появится окно «Добавление ограничения»;
· в поле «Ссылка на ячейку» введите адреса ячеек переменных $B$3:$D$3;
· в поле знака откройте список предлагаемых знаков и выберите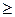 
;
· в поле «Ограничение» введите число 0.
Рис. 4. Добавление условия неотрицательности переменных
7. Аналогичным образом введите оставшиеся ограничения (Рис. 5).
|
|
|
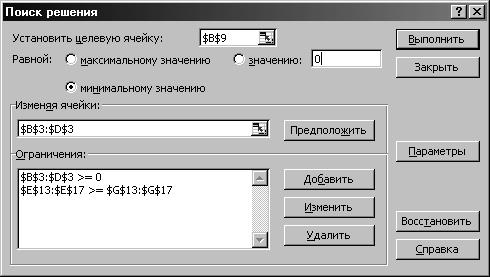
Рис. 5. Ввод ограничений
В нашем случае все ограничения содержат один знак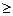 
, поэтому мы ввели ограничение $E$13:$E$17>=$G$13: $G$17. Если же ограничения задачи содержат разные знаки, то каждое ограничение надо вводить отдельно, например, $E$13>=$G$13.
Если при вводе условия задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делают, нажав кнопки «Изменить» или «Удалить».
Задача запускается на решение в окне «Поиск решения» нажатием на кнопку «Выполнить». Но предварительно для установления конкретных параметров решения задач оптимизации необходимо нажать кнопку «Параметры» и заполнить некоторые поля окна «Параметры поиска решения».
8. Установите параметры решения задачи (Рис. 6) и подтвердите установленные параметры нажатием кнопки «OK».
Параметр «Максимальное время» служит для назначения времени (в секундах), выделяемого на решение задачи. В поле можно ввести время, не превышающее 32 767 секунд (более 9 часов).
Параметр «Предельное число итераций» служит для управления временем решения задачи путем ограничения числа промежуточных вычислений. В поле можно ввести количество итераций, не превышающее 32 767.
Рис. 6. Параметры поиска решения, подходящие для большинства задач ЛП
Параметр «Относительная погрешность» служит для задания точности, с которой определяется соответствие ячейки целевому значению или приближение к указанным границам. Поле должно содержать число из интервала от 0 до 1. Чем меньше количество десятичных знаков во введенном числе, тем ниже точность. Высокая точность увеличит время, которое требуется для того, чтобы сошелся процесс оптимизации.
Параметр «Допустимое отклонение» служит для задания допуска на отклонение от оптимального решения в целочисленных задачах. При указании большего допуска поиск решения заканчивается быстрее.
|
|
|
Параметр «Сходимость» применяется только при решении нелинейных задач.
Установка флажка «Линейная модель» обеспечивает ускорение поиска решения линейной задачи за счет применения симплекс-метода.
9. Запустите задачу на решение путем нажатия кнопки «Выполнить».
После запуска на решение задачи ЛП на экране появляется окно «Результаты поиска решения» (Рис. 7 ).
Рис. 7. Сообщение об успешном решении задачи
10. В появившемся окне нажмите кнопку ОК и посмотрите на экране оптимальное решение задачи (Рис. 8).
После запуска на решение задачи ЛП на экране может появиться окно «Результаты поиска решения» с одним из сообщений, представленных на Рис. 9, Рис. 10. Если все данные на предыдущих этапах были внесены верно, то это означает, что оптимальное решение не может быть найдено.
Рис. 8. Экранная форма задачи после получения решения
Рис. 9. Сообщение при несовместной системе ограничений задачи
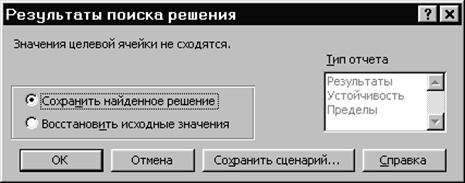
Рис. 10. Сообщение при неограниченности ЦФ в требуемом направлении
Если Вы не смогли найти решение задачи, следовательно, Вы допустили ошибки на предыдущих этапах. Откройте из папки МАТ_МОД файл ошибки.doc и внимательно прочтите приведенную там информацию.
Задание 3
Сохраните файл в своей папке с именем lab_1(a).
Пригласите преподавателя и продемонстрируйте полученный результат.
Допустим, что к условию задачи добавилось требование целочисленности значений всех переменных. В этом случае описанный выше процесс ввода условия задачи необходимо дополнить следующими шагами.
Задание 4
Найдите целочисленное оптимальное решение задачи о дневном рационе, для этого:
· в окне «Поиск решения» (меню «Сервис»®«Поиск решения»), нажмите кнопку «Добавить»;
· в появившемся окне «Добавление ограничений» введите ограничения следующим образом: в поле «Ссылка на ячейку» введите адреса ячеек переменных задачи, то есть $B$3:$D$3;
· в поле ввода знака ограничения установите «целое» (Рис. 11);
Рис. 11. Ввод условия целочисленности переменных задачи
· подтвердите ввод ограничения нажатием кнопки OK и проанализируйте полученный результат (Рис. 12).
Рис. 12. Решение задачи при условии целочисленности ее переменных
Задание 5
Сохраните файл в своей папке с именем lab_1(b).
|
|
|
|
|
|
