Поступательное движение твёрдого тела.

Кинематика материальной точки.

Определение положения точки в пространстве.

 

Для описания движения точки, т.е. изменения ее положения с течением времени, прежде всего, надо в любой момент времени ука­зать ее местоположение координатным или векторным способом. Оба способа задания положения тела в пространстве эквивалентны, т.е. зная координаты точки, можно указать ее радиус-вектор, и наоборот. Из рис. 1 видно, что радиус-вектор представить можно

 

диагональю прямоугольного параллелепипеда со сторонами, численно равными координатам точки Х_а, Y_a и Z_a. Отсюда очевидна связь модуля радиус-вектора точки с ее координатами:

Для определения направления радиус-вектора в пространстве можно определить углы a, b, g, которые радиус-вектор образует с координатными осями OX, OY, и OZ соответственно. Тогда:

 

Таким образом, зная координаты точки, можно определить величину (1) радиус-вектора, и его направление в пространстве по так называемым направляющим косинусам (2), (3) и (4).

При движении точки ее координаты и радиус-вектор с течением времени изменяются, для определения характеристик движения вводят три вектора: перемещения, скорости и ускорения.

ВЕКТОР ПЕРЕМЕЩЕНИЯ.

 

 

Рис. 2

Для определения перемещения точки в пространстве вводят вектор перемещения.

Например, за промежуток времени Dt точка перемещается из положения 1 в положение 2 (рис. 2), определяемые векторным способом указанием радиус-векторов и; вектором перемещения называют вектор, проведенный из начального положения 1 в конечное 2 перемещаемого тела. Из векторного треугольника видно, что вектор перемещения равен приращению радиус-вектора точки.

 

Наряду с изменением радиус-вектора точки происходит изменение ее координат, т.е. перемещение точки вдоль отдельных координатных направлений. Из рис.3 видно, что

 

 

 

Вектор перемещения за конечный промежуток времени в общем случае не совпадает с направлением движения (направлением касательной к траектории движения). Очевидно, что эти направления будут совпадать в общем случае движения только для бесконечно малых перемещений точки.

 

ВЕКТОР СКОРОСТИ.

Вектором скорости называют вектор, определяющий быстроту и направление движения.

Вектором средней скорости называют отношение вектора перемещения к промежутку времени, за который это перемещение происходит:

 

Так как в произвольном случае движения вектор перемещения за конечный промежуток времени не определяет точно направление движения, это не может сделать и вектор средней скорости. Следо­вательно, необходимо рассматривать перемещения за бесконечно ма­лые промежутки времени.

Вектором истинной (мгновенной) скорости называют предел, к которому стремится значение вектора средней скорости при бесконечном убывании промежутка времени:

Так как при движении тела в общем случае изменяются все три его координаты, часто бывает удобным рассматривать скорость дви­жения точки вдоль отдельных координатных направлений (компоненты или составляющие вектора скорости). Компоненты средней скорости равны:

 

 

Компоненты же мгновенной скорости определяются как

 

 

Вектор скорости с его компонентами связан такими же по виду соотношениями, как радиус-вектор с

 

координатами точек:

 

ВЕКТОР УСКОРЕНИЯ.

 

 

Вектором ускорения называют вектор, определяющий быстроту и направление изменения вектора

скорости. Аналогично определени­ям для вектора скорости вводятся понятия среднего и мгновенного

ускорения:

 

При движении точки по произвольной траектории вектор изме­нения скорости ΔJ и, следовательно, вектор ускорения направлены в сторону вогнутости траектории независимо от того, увели­чивается или уменьшается величина скорости (рис. 4, 5):

Рис. 4. Ускоренное движение Рис. 5. Замедленное движение

Как видно из рисунков, в обоих случаях вектор dJ направлен в сторону вогнутости траектории. При ускоренном движении он отклоняется в сторону движения, при замедленном - в противоположную

Для определения мгновенного ускорения надо рассматривать бесконечно малые перемещения, т.е. векторы скорости J₁ и J₂ в соседних точках траектории. Поэтому вектор ускорения лежит в плоскости, содержащей касательную к траектории в данной точке и прямую, параллельную касательной в соседней точке траектории. Такая плоскость называется соприкасающейся. Поэтому наряду с представлением вектора ускорения компонентами

 

 

 

можно рассматривать составляющие вектора в соприкасающейся плос­кости (т.е. только две компоненты). Для определения этих составляющих в любой точке траектории проводят соприкасавшуюся плос­кость и в ней две оси - нормальную O_n. в сторону вогнутости тра­ектории и касательную O_t по касательной к траектории. Изменение скорости и, соответственно, ускорение можно рассматривать в про­екциях на эти оси (рис. 6).

Двигаясь вдоль траектории, за промежуток времени Dt точка про­ходит путь DS скорость ее изменяется от J до J₁, при этом J₁ составляет угол Da (альфа) с осью O_t. По определению мгновенного ускорения:

Рис. 6

 

 

 

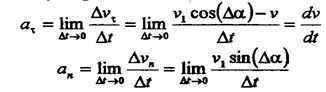Преобразуем выражение предела, умножив и разделив его на Da и DS:

 

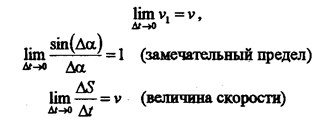Отметим, что при Dt=0 бесконечно убывает и пройденный путь, и угол (DS=0, Da=0). При этом условии значения пределов равны:

 

Предел же называется кривизной траектории К. Кривизна траектории обратно

 

пропорциональна радиусу кривизны траектории:

 

 

С учетом этих замечаний выражение для нормальной составляющей вектора ускорения принимает вид

 

 

Для выяснения физического смысла ускорения рассмотрим два частных случая движения.

Равномерное криволинейное движение (V=const, k<>0). В этом случае, как видно из (14) и (16),

 

Неравномерное прямолинейное движение (V<>соnst, K=0). При таком движении

 

Следовательно, касательная составляющая ускорения определяет изменение вектора скорости по величине, а нормальная - по направлению.

 

Кинематика твердого тела.

Для нахождения кинематического закона движения, т.е. r=r(t) или х = х(t), у=y(t), z=z(t) надо найти закон движения каждой точки тела, т.е. решить бесконечно большое число уравнений, что сопряжено с непреодолимыми математическими трудностями.

Однако особенности самого твердого тела и особенности его движения могут значительно упростить задачу.

ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ.

 

Числом степеней свободы называют число независимых механичес­ких координат полностью и однозначно определяющих положение тела в пространстве. Или: число независимых механических движений, которые одновременно может совершать тело.

Из таких определений следует, что число степеней свободы для свободной материальной точки равно 3. Для совокупности из n невзаимодействующих между собой точек число степеней свободы равно 3n.

Любые связи (взаимодействия) ограничивают число степеней сво­боды. Например, точка двигается по поверхности, задаваемой уравнением F(x,y,z)=0. В этом случае необходимо задать независимо 2 координаты, третья же не является независимой - она определяет­ся из уравнения поверхности, по

 

 

которой движется точка. Иначе говоря, для точки, движущейся по поверхности, число степеней сво­боды равно 2. Для точки, движущейся вдоль линии, число степеней свободы равно 1. Действительно, любую линию можно пересечением двух поверхностей, т.е. для определения положения точки в пространстве нужно указать независимо только одну координату, две другие же определяются из уравнения линии.

Рассмотрим теперь систему точек, связанных жесткими связями. Пусть таких точек 2 (рис. 7). Для определения положения одной из точек системы в пространстве нужно указать 3 координаты, т.е. эта часть системы обладает 3-мя степенями свободы. Если эту точ­ку закрепить неподвижно, у системы будет отнято 3 степени свободы. Вторая точка при этом может двигаться только по поверхности сферы, т.е. обладает 2-мя степенями свободы. Следовательно, вся система обладает 5-ю степенями свободы.

 

 

Рис. 7 Рис. 8

 

Аналогично определяется число степеней свободы для системы, состоящей из трех жестко связанных между собой точек (рис. 8). Если одну из точек системы закрепить, у системы отнимается 3 степени свободы При закреплении второй точки дополнительно отнимается еще а степени свободы При этом третья точка сможет двигать­ся только вдоль линии, т.е. обладает одной степенью свободы. поэтому вся система обладает 6-ю степенями свободы. Легко убедиться» что добавляя к такой системе 4-ю, 5-ю и т.д. точки, мы не увеличим число степеней свободы, т.е. максимальное число степеней свободы для системы жестко связанных между собой точек равно. Абсолютно твердое тело как раз представляет собой такую систему, следовательно, обладает 6-ю степенями свободы.

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТВЁРДОГО ТЕЛА.

Поступательным называют такое движение твердого тела, при котором любая прямая, проведенная в теле, при движении тела остается параллельной самой себе. Будем рассматривать движение абсолютно твердого тела. Выделим в теле произвольно т. т. А₁ и В₁. Через промежуток времени Dt они займут положения А₂ и В₂ соответственно (рис. 9).

 

 

Рис. 9

 

Эти положения можно задать векторным способом, указав радиус-векторы r_a1, r_b1, r_a2, r_b2. Перемещения точек равны Dr_a, и Dr_b. Векторы (A₁B₁)и (A₂B₂) равны между собой, так как равны их модули (тело абсолютно твердое) и одинаковы направления (тело перемещается поступательно).

 

 

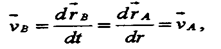Поэтому перемещения точек А и В равны (Dr_a = Dr_b) Поскольку точ­ки выбирались произвольно, можно сделать вывод, что при поступательном движении тела все его точки совершают одинаковые перемещения. По определению:

 

 

т.е. и скорости всех точек тела одинаковы. Аналогично можно пока­зать, что и ускорения всех точек тела одинаковы. Следовательно, при поступательном движении все точки тела движутся одинаково и для описания движения тела достаточно рассмотреть движение только одной его точки (чаще всего центра масс тела). Пример поступа­тельного движения - движение кузова автомобиля на прямолинейном участке дороги.

12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: