 |
Свойства линейного пространства
|
|
|
|
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
Определение линейного пространства
Определение. Множество X элементов x, y, z, … называется линейным пространством, если выполнены условия:
1) задано сложение элементов множества X, т. е. задан закон, по которому любым двум элементам x и y множества Х ставится в соответствие элемент z этого множества, называемый суммой элементов x и y и обозначаемый z = x + y;
2) задано умножение элемента на число, т. е. задан закон, по которому любому элементу х множества Х и любому вещественному числу l ставится в соответствие элемент z ÎX, называемый произведением элемента х на число l и обозначаемый z = l x;
3) указанные линейные операции (законы) подчиняются аксиомам линейного пространства:
а) x + y = y + x (коммутативность сложения);
б) (x + y) + z = x + (y + z) (ассоциативность сложения);
в) существует элемент 0 Î X такой, что для любого элемента х множества Х выполняется равенство х+ 0 =х;
г) для любого элемента х множества Х найдется элемент (– х)Î X такой, что х + (– х) = 0;
д) для любого элемента х множества Х выполняется условие 1 × х = х;
е) для любого элемента х множества Х и любых чисел l и m имеет место ассоциативность умножения на число, т. е. l(m х) = = (lm) х;
ж) умножение на число и сложение связаны законом дистрибутивности по числам (l + m) х = l х + m х;
з) умножение на число и сложение связаны законом дистрибутивности по элементам l(x + y) = l х + l у.
Элементы линейного пространства принято называть векторами. Элемент 
называется нулевым вектором, а элемент 
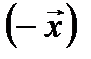– противоположным элементом к вектору 
.
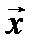Фактически линейное пространство – это совокупность множества элементов и двух операций, введенных на этом множестве.
Согласно определению линейного пространства сумма определена для любых элементов из множества Х и сама является элементом этого пространства. Говорят, что множество Х замкнуто относительно операции сложения. Так как для любого элемента линейного пространства определена операция умножения на число, результат которой также принадлежит этому пространству, то линейное пространство замкнуто относительно умножения на число.
|
|
|
В качестве линейных пространств можно рассмотреть множество матриц размера т´п, элементами которых являются вещественные числа, относительно матричных операций сложения и умножения на число; множество всех свободных векторов на плоскости или в пространстве с линейными операциями над векторами и т.д.
Пример. Множество R всех вещественных чисел есть линейное пространство. Множество R+ положительных вещественных чисел не является линейным пространством, потому что при умножении любого его элемента на отрицательное число или на нуль полученный элемент уже не будет принадлежать R+.
Однако можно ввести такие операции «сложения» и «умножения на число», что множество R+ будет образовывать линейное пространство. Любой паре положительных чисел а и b поставим в соответствие число ab, которое назовем их «суммой», а произведением элемента а из множества R+ на вещественное число l назовем положительное число 
, т. е. 
и 
.
Проверим выполнение аксиом линейного пространства:
a) коммутативность сложения:
;
б) ассоциативность сложения:
;
в) нейтральным элементом по сложению является 1:
г) для любого положительного числа 
противоположный элемент по сложению ˗ число 
:
д) для любого вещественного положительного числа 
выполняется условие
;
е) ассоциативность умножения на число:
;
ж) дистрибутивность по числам:
;
з) дистрибутивность по элементам:
.
Свойства линейного пространства
1. Любое линейное пространство имеет только один нулевой вектор.
|
|
|
Доказательство. Доказательство проведем методом от противного. Предположим, что существуют два нулевых вектора 
и 
, причем 
. Тогда 
(так как 
– нулевой вектор). По аксиоме линейного пространства о коммутативности сложения, учитывая, что 
– нулевой вектор, имеем: 
. Получили противоречие, свойство доказано.
2. Любой вектор линейного пространства имеет только один противоположный вектор.
Доказательство. Доказательство проведем методом от противного. Предположим, что существуют два противоположных элемента 
и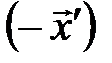 
к элементу 
, причем 
. Тогда 
. Получили противоречие с предположением о том, что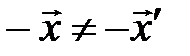 
. Утверждение доказано.
3. Если вектор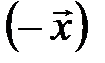 
противоположен вектору 
, то вектор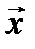 
противоположен вектору 
.
Доказательство. Рассмотрим четыре утверждения: (I) вектор 
противоположен вектору 
; (II) 
; (III) вектор 
противоположен вектору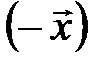 
; (IV) 
. Тогда (I) 
(II), (III) 
(IV). Однако утверждения (II) и (IV) эквивалентны, следовательно, утверждения (I) и (III) эквивалентны. Свойство доказано.
4. Для любых векторов 
и 
уравнение 
имеет решение и притом единственное.
Доказательство. Покажем, что решением уравнения является вектор 
: 
. Докажем единственность такого решения. Пусть 
– произвольное решение уравнения 
. Тогда 
, или 
, т. е. произвольное решение совпадает с указанным ранее. Свойство доказано.
Определение.Разностью двух векторов 
называется вектор 
, являющийся решением уравнения 
, т. е. 
.
5. Произведение любого элемента линейного пространства на число 0 равно нулевому вектору.
Доказательство. Рассмотрим уравнение 
. Решением 
уравнения будет нулевой вектор. С другой стороны, решением этого уравнения является вектор 
, так как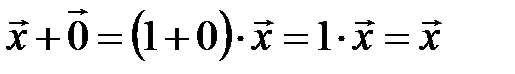 
, таким образом, вектор 
совпадает с нулевым вектором.
6. Вектор, противоположный вектору 
, равен произведению вектора 
на 
.
Доказательство. Рассмотрим вектор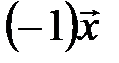 
. Тогда по свойству 5: 
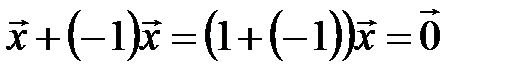. Вектор 
удовлетворяет аксиоме линейного пространства о существовании противоположного (обратного) элемента, следовательно,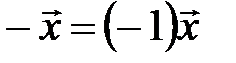 
.
7. Произведение нулевого вектора на любое число есть нулевой вектор.
Доказательство. Учитывая, что 
, возьмем в качестве вектора 
нулевой вектор. Имеем 
. Свойство доказано.
|
|
|
