 |
Нормированные пространства
|
|
|
|
Норма - обобщение длины свободного вектора. Длину вектора в линейном пространстве 
или 
можно рассматривать как функцию, определенную на множестве или , которая каждому вектору рассматриваемого линейного пространства ставит в соответствие его длину.
Норму вектора в линейном пространстве иногда называют длиной.
Определение. Заданная на линейном пространстве 
функция, которая каждому вектору 
из ставит в соответствие действительное число 
, называется нормой, если она удовлетворяет аксиомам нормы:
a) 
, причем 
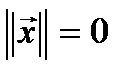, если 
;
б) 
, 
, 
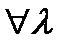R;
в) 
- неравенство треугольника.
Определение. Линейное пространство, в котором задана норма, называется нормированным пространством.
Евклидовы и нормированные пространства являются линейными пространствами с дополнительными структурами: скалярным умножением и нормой соответственно.
Теорема. Всякое скалярное умножение в евклидовом пространстве 
определяет норму согласно формуле
. (3.4)
Доказательство. Так как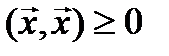 
, то функция определена для любого вектора 
евклидова пространства 
. Проверим выполнение аксиом нормы:
a) 
, так как 
, причем 
, если ;
б) 
;
в) из неравенства Коши ˗ Буняковского 
следует, что 
или 
. Тогда 
. 
. Таким образом, 
. Теорема доказана.
Введение нормы по формуле (3.4) опирается только на общие свойства скалярного произведения, поэтому норму, определяемую равенством (3.4), называют евклидовой, или сферической.
Ортогональное дополнение
Любое линейное подпространство Н в линейном пространстве L имеет прямое дополнение 
такое, что 
. Такое линейное подпространство не единственное. Однако евклидово пространство представляет собой особый случай.
Определение. Ортогональным дополнением линейного подпространства Н в евклидовом пространстве Е называется множество 
всех векторов евклидова пространства, ортогональных каждому из векторов линейного подпространства Н, т. е.
|
|
|
.
Теорема. Ортогональное дополнение 
линейного подпространства 
в евклидовом пространстве 
является линейным подпространством в , причем 
и 
.
Доказательство. Рассмотрим произвольные векторы 
и произвольный вектор 
линейного подпространства . Имеем 
, 
, т. е. 
и 
. Следовательно, 
˗ линейное подпространство в евклидовом пространстве . Пусть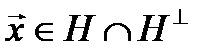 
. Этот вектор ортогонален самому себе, так как, с одной стороны, 
, а с другой, - 
, т. е. вектор 
ортогонален любому вектору из 
. Таким образом, 
. По свойству скалярного произведения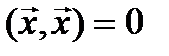 
только в том случае, если 
. Получили, что 
. Это означает, что 
.
Пусть 
- ортонормированный базис в линейном подпространстве . Учитывая, что 
, дополним базис 
до базиса во всем евклидовом пространстве векторами 
. Используя процесс ортогонализации Грама ˗ Шмидта, построим ортонормированный базис 
во всем евклидовом пространстве. Так как первые т векторов попарно ортогональны и имеют единичную длину, то в процессе ортогонализации их оставим без изменения. Векторы 
ортогональны каждому из векторов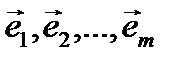 
базиса линейного подпространства 
, поэтому они ортогональны всему подпространству 
, так как его оболочкой служат векторы 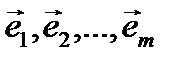. Следовательно, все векторы принадлежат 
. Рассмотрим произвольный вектор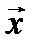 
из евклидового пространства 
и разложим его по базису :
,
где 
, 
, следовательно, 
и 
. Теорема доказана.
Следствие. Каково бы ни было линейное подпространство в евклидовом пространстве , любой вектор 
евклидового пространства можно представить в виде 
, где 
, 
. Это утверждение и означает, что 
.
Определение. Разложение вектора 
на две составляющие 
и 
называется суммой ортогональных проекций вектора 
на линейные подпространства 
и 
. Вектор 
называется ортогональной составляющей вектора 
относительно подпространства 
.
|
|
|
|
|
|
