 |
Размерность линейного пространства
|
|
|
|
Определение. Максимальное количество линейно независимых векторов в данном линейном пространстве называется размерностью линейного пространства.
Пространство Х называется конечномерным, если оно обладает хотя бы одним базисом, состоящим из конечного числа векторов. Это число называется размерностью линейного пространства и обозначается  .
.
Если размерность линейного пространства Х равна п, т. е. существует линейно независимая система из п векторов, а любая система, содержащая п +1 и более векторов, линейно зависимая, то говорят, что линейное пространство п -мерное.
Все п -мерные линейные пространства конечномерны. Однако существуют линейные пространства, в которых можно выбрать линейно независимую систему, содержащую сколь угодно большое количество векторов. Пример такого линейного пространства ˗ система функций, непрерывных на отрезке  : система 1,
: система 1,  ,
, 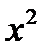 , …,
, …,  линейно независима для любого натурального п, так как линейная комбинация
линейно независима для любого натурального п, так как линейная комбинация  равна нулю только в том случае, если
равна нулю только в том случае, если  ,
, 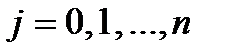 .
.
Теорема. В п -мерном линейном пространстве Х любая линейно независимая система, состоящая из п векторов, является его базисом.
Доказательство. Пусть  ,
,  , …,
, …,  - система линейно независимых векторов в линейном пространстве Х. Согласно определению размерности пространства любые (п +1) векторов будут линейно зависимы. Пусть
- система линейно независимых векторов в линейном пространстве Х. Согласно определению размерности пространства любые (п +1) векторов будут линейно зависимы. Пусть  - произвольный вектор Х, не входящий в базис
- произвольный вектор Х, не входящий в базис  ,
,  , …,
, …, 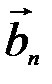 . Тогда существуют вещественные числа α0, α1, …, α n такие, что
. Тогда существуют вещественные числа α0, α1, …, α n такие, что  и
и 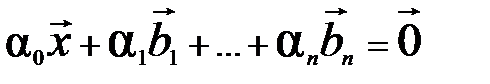 . В этой линейной комбинации
. В этой линейной комбинации 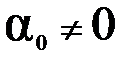 (если
(если  , то
, то  и система векторов
и система векторов  ,
, 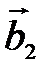 , …,
, …,  будет линейно зависимой), поэтому
будет линейно зависимой), поэтому  , т. е. произвольный вектор
, т. е. произвольный вектор  из Х представляется в виде линейной комбинации линейно независимой системы векторов
из Х представляется в виде линейной комбинации линейно независимой системы векторов  ,
,  , …,
, …,  , следовательно, эта система образует базис. Теорема доказана.
, следовательно, эта система образует базис. Теорема доказана.
|
|
|
Определение. Базисным минором матрицы  называется минор k -го порядка этой матрицы такой, что он отличен от нуля, а все миноры
называется минор k -го порядка этой матрицы такой, что он отличен от нуля, а все миноры  -го порядка равны нулю либо минор
-го порядка равны нулю либо минор  -го порядка не существует.
-го порядка не существует.
Порядок любого базисного минора матрицы совпадает с рангом этой матрицы, причем любой столбец (строка) этой матрицы является линейной комбинацией линейно независимых столбцов (строк) матрицы, в которых расположен базисный минор.
Теорема. Если в линейном пространстве  существует базис из п векторов, то
существует базис из п векторов, то  .
.
Доказательство. Пусть  - базис в
- базис в 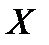 . Достаточно показать, что любая система векторов
. Достаточно показать, что любая система векторов  ,
,  , …,
, …,  ,
,  будет линейно зависимой. Разложим каждый из этих векторов по базису
будет линейно зависимой. Разложим каждый из этих векторов по базису  :
:
 ,
, 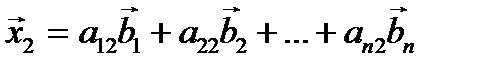 ,
,
……………………….., 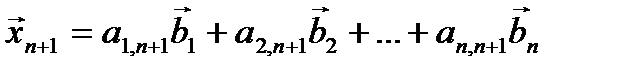 .
.
Составим матрицу из столбцов координат:  . Линейная зависимость системы векторов
. Линейная зависимость системы векторов  ,
,  , …,
, …, 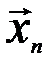 ,
,  равносильна линейной зависимости столбцов матрицы
равносильна линейной зависимости столбцов матрицы  . В матрице
. В матрице 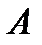 n строк и n+ 1 столбец, следовательно,
n строк и n+ 1 столбец, следовательно,  , поэтому столбцы линейно зависимы и линейно зависима система векторов
, поэтому столбцы линейно зависимы и линейно зависима система векторов  ,
,  , …,
, …, 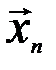 ,
,  , т. е.
, т. е.  . Теорема доказана.
. Теорема доказана.
Следствие. В любом п -мерном линейном пространстве Х два базиса содержат одно и то же количество векторов, которое совпадает с размерностью линейного пространства Х.
Пример. Показать, что векторы  ,
,  и
и  , заданные своими координатами в одном и том же базисе, сами образуют базис.
, заданные своими координатами в одном и том же базисе, сами образуют базис.
Решение. Каждый из векторов имеет три координаты, т. е. в линейном пространстве имеется базис из трех векторов. Поэтому любая линейно независимая система из трех векторов образует базис. Проверим, что данные векторы линейно независимые. Составим матрицу, столбцами которой являются координаты векторов и найдем ее ранг:
 ~
~  ~
~  .
.
Ранг матрицы равен трем, следовательно, ее столбцы линейно независимы, и, соответственно, векторы линейно независимы и образуют базис.
Преобразование координат вектора
При замене базиса
|
|
|
Пусть  - п -мерное линейное пространство, в котором заданы два базиса
- п -мерное линейное пространство, в котором заданы два базиса 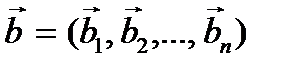 и
и 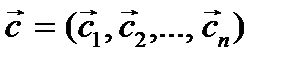 . Так как векторы
. Так как векторы  образуют базис, то любой вектор из базиса
образуют базис, то любой вектор из базиса  может быть представлен в виде
может быть представлен в виде  ,
,  . Следовательно, базис
. Следовательно, базис  выражается через базис
выражается через базис 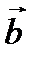 следующим образом:
следующим образом:
 ,
,
или  , (1.3)
, (1.3)
где 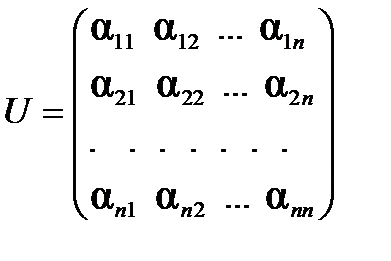 .
.
Определение. Матрица  , столбцами которой являются координаты векторов из базиса
, столбцами которой являются координаты векторов из базиса  в базисе
в базисе 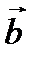 , называется матрицей перехода от старого базиса
, называется матрицей перехода от старого базиса 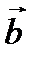 к новому базису
к новому базису 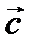 .
.
Матрицы перехода обладают следующими свойствами.
1. Матрица перехода  - невырожденная, т. е.
- невырожденная, т. е.  .
.
Доказательство. Столбцами матрицы  являются столбцы координат векторов нового базиса в старом. Векторы базиса линейно независимы, следовательно, столбцы матрицы линейно независимы и
являются столбцы координат векторов нового базиса в старом. Векторы базиса линейно независимы, следовательно, столбцы матрицы линейно независимы и  . Свойство доказано.
. Свойство доказано.
2. Если в линейном п -мерном пространстве 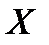 задан базис
задан базис  и существует невырожденная матрица
и существует невырожденная матрица  , то в линейном пространстве
, то в линейном пространстве  существует базис
существует базис  такой, что матрица
такой, что матрица  будет матрицей перехода от базиса
будет матрицей перехода от базиса  к базису
к базису  .
.
Доказательство. Определитель  отличен от нуля, следовательно,
отличен от нуля, следовательно, 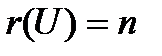 , ее столбцы базисные и линейно независимые. Эти столбцы являются столбцами координат системы векторов
, ее столбцы базисные и линейно независимые. Эти столбцы являются столбцами координат системы векторов  , т. е.
, т. е.  . Столбцы линейно независимы, таким образом, система векторов
. Столбцы линейно независимы, таким образом, система векторов  линейно независима и содержит п векторов. Любые п линейно независимых вектора в п -мерном пространстве являются базисом, следовательно, система векторов
линейно независима и содержит п векторов. Любые п линейно независимых вектора в п -мерном пространстве являются базисом, следовательно, система векторов  - базис. Свойство доказано.
- базис. Свойство доказано.
3. Если 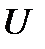 - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  в линейном пространстве, то
в линейном пространстве, то  - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису 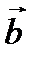 .
.
Доказательство. Если 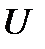 - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  в линейном пространстве, то
в линейном пространстве, то  и, следовательно, существует обратная матрица
и, следовательно, существует обратная матрица  . Умножим равенство
. Умножим равенство  на матрицу
на матрицу  справа. Имеем
справа. Имеем  , т. е.
, т. е.  - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису 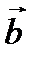 . Свойство доказано.
. Свойство доказано.
4. Если в линейном пространстве  заданы базисы
заданы базисы  ,
,  ,
, 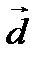 и
и  ,
,  , то
, то  - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  .
.
Доказательство.  , т. е.
, т. е.  - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  . Свойство доказано.
. Свойство доказано.
Рассмотрим произвольный вектор  линейного пространства
линейного пространства  , в котором заданы два базиса:
, в котором заданы два базиса: 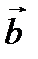 (старый) и
(старый) и 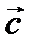 (новый). Пусть этот вектор имеет координаты
(новый). Пусть этот вектор имеет координаты  и
и  в базисах
в базисах 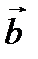 и
и 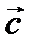 соответственно, т. е.
соответственно, т. е.  и
и  . Если
. Если 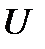 - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  , то
, то  . Из единственности разложения вектора в одном и том же базисе следует, что
. Из единственности разложения вектора в одном и том же базисе следует, что  , или
, или
|
|
|
 . (1.4)
. (1.4)
Формула (1.4) устанавливает связь между координатами одного и того же вектора в двух различных базисах одного и того же линейного пространства.
Пример. Даны два базиса  и
и  . Найти связь координат одного и того же вектора в этих двух базисах, если
. Найти связь координат одного и того же вектора в этих двух базисах, если  ,
,  ,
, 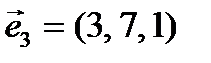 ,
, 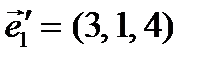 ,
,  ,
, 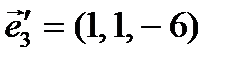 .
.
Решение. Для того чтобы найти матрицу  перехода от базиса
перехода от базиса  к базису
к базису  , надо решить уравнение
, надо решить уравнение  , которое в матричной форме имеет вид
, которое в матричной форме имеет вид 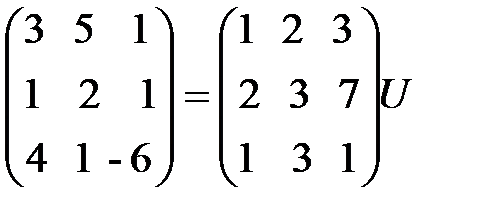 . Из этого уравнения находим матрицу перехода:
. Из этого уравнения находим матрицу перехода:
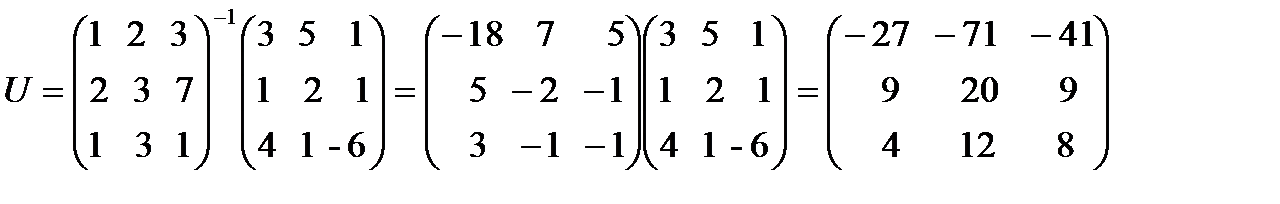 .
.
Тогда связь координат одного и того же вектора в этих двух базисах определяется соотношениями  или
или  ,
,  ,
,  .
.
Пример. Найти координаты вектора 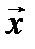 в базисе
в базисе  , если известны его координаты
, если известны его координаты  в базисе
в базисе 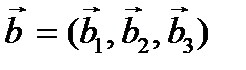 и
и  ,
, 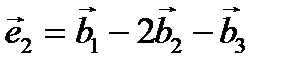 ,
,  .
.
Решение. Координаты базиса  заданы в базисе
заданы в базисе 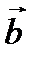 , поэтому матрицей
, поэтому матрицей  перехода от базиса
перехода от базиса 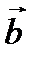 к базису
к базису  будет матрица, столбцами которой являются координаты векторов базиса
будет матрица, столбцами которой являются координаты векторов базиса  в базисе
в базисе 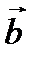 , т. е.
, т. е.  . Поэтому
. Поэтому  , где
, где  и
и 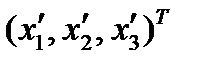 - координаты вектора
- координаты вектора  в базисах
в базисах  и
и  соответственно. Определитель матрицы перехода
соответственно. Определитель матрицы перехода  отличен от нуля, поэтому
отличен от нуля, поэтому  , т. е. вектор
, т. е. вектор  в базисе
в базисе  имеет координаты
имеет координаты  .
.
ЛИНЕЙНЫЕ ПОДПРОСТРАНСТВА
|
|
|


