 |
Линейная зависимость элементов
|
|
|
|
Линейного пространства
Пусть векторы  являются элементами линейного пространства. С помощью линейных операций (сложения и умножения на число) составим выражение вида
являются элементами линейного пространства. С помощью линейных операций (сложения и умножения на число) составим выражение вида
 , (1.1)
, (1.1)
где  – вещественные числа. Выражение (1.1) называется линейной комбинацией векторов
– вещественные числа. Выражение (1.1) называется линейной комбинацией векторов  , а числа
, а числа  – коэффициентами линейной комбинации. Если
– коэффициентами линейной комбинации. Если  , то комбинация называется тривиальной. Если существует номер
, то комбинация называется тривиальной. Если существует номер 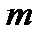 ,
,  такой, что
такой, что  , то линейная комбинация называется нетривиальной.
, то линейная комбинация называется нетривиальной.
Определение. Конкретный набор векторов  из линейного пространства Х называется системой векторов, а любая его часть – подсистемой.
из линейного пространства Х называется системой векторов, а любая его часть – подсистемой.
Определение. Система векторов  в линейном пространстве Х называется линейно зависимой (говорят, что векторы линейно зависимы), если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т. е. векторы
в линейном пространстве Х называется линейно зависимой (говорят, что векторы линейно зависимы), если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору, т. е. векторы  линейно зависимы, если найдутся вещественные числа
линейно зависимы, если найдутся вещественные числа 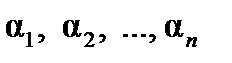 , удовлетворяющие условию
, удовлетворяющие условию 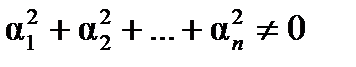 , такие, что
, такие, что  .
.
Теорема. Для того чтобы система векторов  была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных, т. е. векторы
была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных, т. е. векторы  ,
, 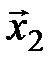 , …,
, …, 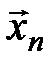 линейно зависимы тогда и только тогда, когда существует номер
линейно зависимы тогда и только тогда, когда существует номер 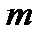 ,
,  такой, что выполняется равенство
такой, что выполняется равенство  .
.
Доказательство. А) Необходимость. Пусть векторы  линейно зависимы. Тогда существуют вещественные числа
линейно зависимы. Тогда существуют вещественные числа 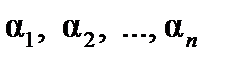 , не равные одновременно нулю, такие, что
, не равные одновременно нулю, такие, что  . Для определенности будем считать, что
. Для определенности будем считать, что  (
( ). Тогда
). Тогда
 .
.
Введем обозначения:  , (
, ( ). С учетом этих обозначений вектор
). С учетом этих обозначений вектор  представляется в виде
представляется в виде  , т. е. является линейной комбинацией остальных векторов.
, т. е. является линейной комбинацией остальных векторов.
Б) Достаточность. Пусть вектор 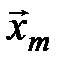 представляется в виде
представляется в виде  . Следовательно,
. Следовательно, 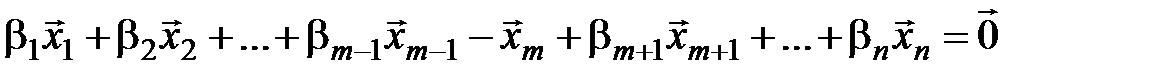 . Эта линейная комбинация, равная нулевому вектору, является нетривиальной, так как коэффициент перед
. Эта линейная комбинация, равная нулевому вектору, является нетривиальной, так как коэффициент перед  равен –1, поэтому векторы
равен –1, поэтому векторы  ,
, 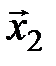 , …,
, …,  линейно зависимы. Теорема доказана.
линейно зависимы. Теорема доказана.
|
|
|
Свойства систем векторов
Из аксиом линейного пространства следуют простейшие свойства систем векторов  ,
,  , …,
, …,  произвольного линейного пространства Х.
произвольного линейного пространства Х.
1. Если существует такой номер  , что
, что 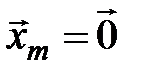 , то система векторов
, то система векторов  ,
,  , …,
, …,  линейно зависима.
линейно зависима.
Доказательство. Составим линейную комбинацию векторов  ,
,  , …,
, …,  :
:  . Эта линейная комбинация равна нулевому вектору и не является тривиальной, следовательно, система векторов линейно зависима.
. Эта линейная комбинация равна нулевому вектору и не является тривиальной, следовательно, система векторов линейно зависима.
Свойство доказано.
2. Если система векторов содержит линейно зависимую подсистему, то система линейно зависима.
Доказательство. В системе векторов 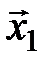 ,
,  , …,
, …, 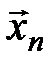 линейного пространства Х выделим линейно зависимую подсистему
линейного пространства Х выделим линейно зависимую подсистему 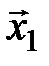 ,
,  , …,
, …,  (
( ). Тогда существуют числа
). Тогда существуют числа  ,
,  , …,
, …, 
 такие, что
такие, что  .
.
Рассмотрим линейную комбинацию 
 , в которой
, в которой  . Эта линейная комбинация равна нулевому вектору и не является тривиальной, так как
. Эта линейная комбинация равна нулевому вектору и не является тривиальной, так как  , следовательно, система векторов
, следовательно, система векторов  ,
,  , …,
, …,  линейно зависима. Свойство доказано.
линейно зависима. Свойство доказано.
3. Если система векторов линейно независима, то любая ее подсистема линейно независима.
Доказательство. Доказательство проведем от противного. Пусть в линейно независимой системе векторов  ,
,  , …,
, …,  линейного пространства Х подсистема векторов
линейного пространства Х подсистема векторов  ,
, 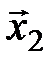 , …,
, …,  (
( ) является линейно зависимой. Тогда по предыдущему свойству вся система линейно зависима. Пришли к противоречию с предположением, что система векторов линейно независима.
) является линейно зависимой. Тогда по предыдущему свойству вся система линейно зависима. Пришли к противоречию с предположением, что система векторов линейно независима.
Свойство доказано.
4. Если векторы  ,
,  , …,
, …, 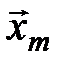 линейного пространства Х линейно независимы, а вектор
линейного пространства Х линейно независимы, а вектор  ,
,  Х не является линейной комбинацией векторов
Х не является линейной комбинацией векторов 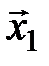 ,
,  , …,
, …,  , то расширенная система векторов
, то расширенная система векторов  ,
,  , …,
, …,  ,
,  линейно независима.
линейно независима.
Доказательство. Доказательство проведем от противного. Пусть расширенная система векторов  ,
, 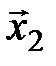 , …,
, …,  ,
, 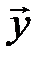 линейно зависима, т. е. существует нетривиальная линейная комбинация
линейно зависима, т. е. существует нетривиальная линейная комбинация 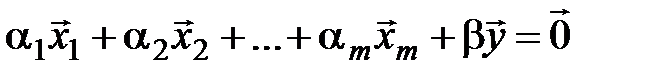 . Коэффициент
. Коэффициент  равен нулю (в противном случае вектор
равен нулю (в противном случае вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  ,
, 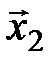 , …,
, …, 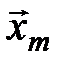 ). Тогда
). Тогда  , и векторы
, и векторы  ,
, 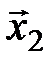 , …,
, …,  будут линейно независимы, если
будут линейно независимы, если  . Следовательно, линейная комбинация
. Следовательно, линейная комбинация  , равная нулевому вектору, является тривиальной. Получили противоречие с предположением существования нетривиальной линейной комбинации
, равная нулевому вектору, является тривиальной. Получили противоречие с предположением существования нетривиальной линейной комбинации 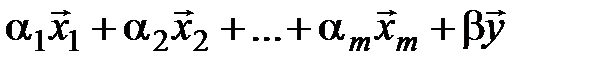 , равной нулевому вектору. Свойство доказано.
, равной нулевому вектору. Свойство доказано.
|
|
|
Пример. Рассмотрим векторы 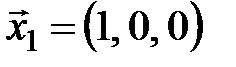 ,
,  ,
,  в трехмерном пространстве. Составим линейную комбинацию этих векторов
в трехмерном пространстве. Составим линейную комбинацию этих векторов 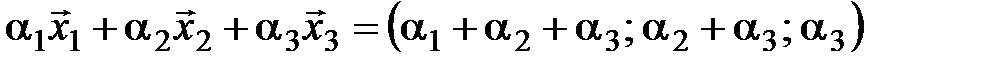 . Эта линейная комбинация будет равна нулевому вектору, если выполняются условия:
. Эта линейная комбинация будет равна нулевому вектору, если выполняются условия: 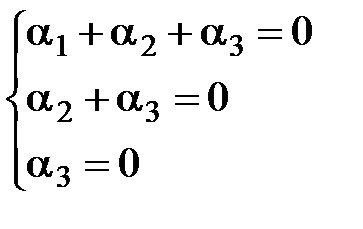 . Система линейных однородных уравнений относительно
. Система линейных однородных уравнений относительно  ,
,  и
и  имеет единственное нулевое решение. Следовательно, линейная комбинация векторов
имеет единственное нулевое решение. Следовательно, линейная комбинация векторов 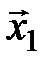 ,
,  ,
,  , равная нулевому вектору, будет тривиальной, т. е. векторы линейно независимы.
, равная нулевому вектору, будет тривиальной, т. е. векторы линейно независимы.
|
|
|


