Базис линейного пространства

Определение. Базисом линейного пространства Х называется упорядоченная система векторов, для которой выполнены условия: а) эта система векторов линейно независима; б) любой вектор линейного пространства Х может быть представлен в виде линейной комбинации векторов этой системы.

Пусть векторы , , …, образуют базис в линейном пространстве Х. Тогда любой вектор , Х, может быть представлен в виде

. (1.2)

Формула (1.2) называется разложением вектора по базису .

Теорема. В произвольном линейном пространстве Х разложение любого вектора по данному базису единственно.

Доказательство. Пусть , , …, - базис в линейном пространстве Х и вектор имеет два разложения по этому базису, т. е. . и . . Найдем разность этих векторов, используя аксиомы линейного пространства: . Так как система векторов , , …, линейно независима, то , , т. е. два разложения вектора в одном и том же базисе совпадают. Теорема доказана.

Замечание. Условие линейной независимости векторов базиса означает, что нулевой вектор в этом базисе имеет единственное разложение – тривиальное. Из единственности разложения нулевого вектора следует единственность разложения любого вектора по базису.

Определение. Коэффициенты разложения вектора по базису линейного пространства Х, записанные в соответствии с порядком векторов в базисе, называются координатами вектора в данном базисе.

При изменении порядка векторов в базисе получается новый базис.

Базис 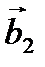, …, в данном линейном пространстве Х удобно записывать как матрицу-строку , а координаты вектора в этом базисе – как матрицу-столбец . Тогда , т. е. разложение вектора по базису , , 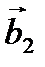…, можно записать как произведение матрицы-строки на матрицу-столбец.

Пример. Рассмотрим в трехмерном пространстве вектор , координаты которого заданы в базисе, состоящем из векторов , , . Имеем .

Теорема. При сложении в линейном пространстве Х любых двух векторов их координаты в одном и том же базисе складываются, а при умножении вектора на число – его координаты умножаются на это число.

Доказательство. Пусть 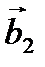, …, – базис в линейном пространстве Х, в котором даны разложения векторов и : , . С использованием аксиом линейного пространства можно записать: . В матричной форме , , . Аналогично доказывается, что при умножении вектора на число его координаты умножаются на это число. Теорема доказана.

Следствие. Линейная зависимость (независимость) векторов линейного пространства эквивалентна линейной зависимости (независимости) столбцов их координат в одном и том же базисе данного линейного пространства.

Определение.Стандартным базисом в пространстве Rⁿ называется базис, образованный векторами , , …, .

Пример. Показать, что векторы , и образуют базис, и найти в этом базисе координаты вектора .

Решение. Для того чтобы доказать, что векторы , , образуют базис, надо показать, что эти векторы линейно независимы и любой вектор в пространстве R³ является их линейной комбинацией. Запишем в стандартном базисе , и столбцы координат векторов , , , и 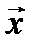: , , , , . Из столбцов координат векторов , , составим матрицу . Определитель этой матрица равен 9, т. е. матрица невырожденная, следовательно, все ее столбцы линейно независимы, поэтому векторы , , линейно независимы. Рассмотрим систему линейных алгебраических уравнений, имеющую в матричной записи вид , где . Эта система всегда имеет единственное решение относительно неизвестных , 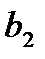и (по теореме Крамера), поэтому любой вектор является линейной комбинацией векторов , , , т. е. эти векторы образуют базис. В качестве произвольного вектора можно взять вектор . В этом случае относительно , 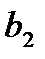и имеем систему уравнений . Решением этой системы будут , , , которые являются координатами вектора в базисе , , .