 |
Характеристическое уравнение матрицы
|
|
|
|
Пусть 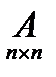 - произвольная матрица. Рассмотрим определитель
- произвольная матрица. Рассмотрим определитель  матрицы
матрицы 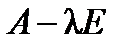 , где
, где 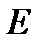 - единичная матрица п -го порядка,
- единичная матрица п -го порядка, 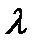 - действительное переменное:
- действительное переменное: 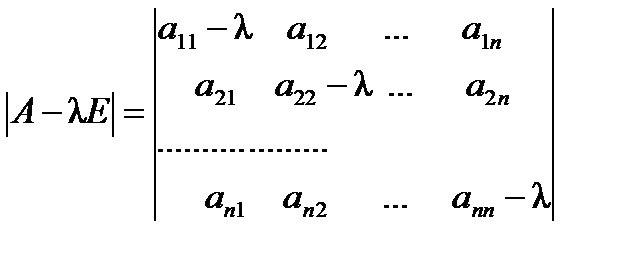 . Относительно
. Относительно 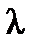 этот определитель является многочленом степени п и может быть записан в виде
этот определитель является многочленом степени п и может быть записан в виде 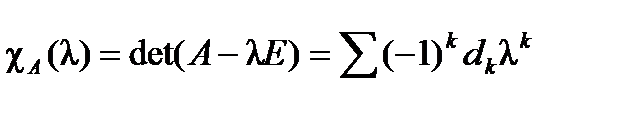 . В этом выражении коэффициенты
. В этом выражении коэффициенты 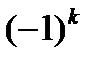 введены для удобства.
введены для удобства.
Определение. Многочлен 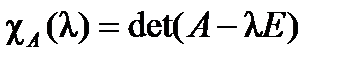 называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы 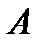 , а уравнение
, а уравнение 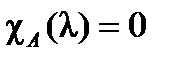 . - характеристическим уравнением матрицы
. - характеристическим уравнением матрицы 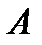 .
.
Пример. Написать характеристический многочлен 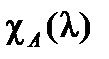 матрицы
матрицы 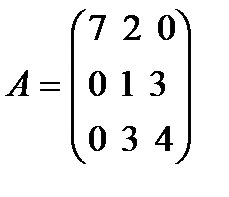 .
.
Решение. 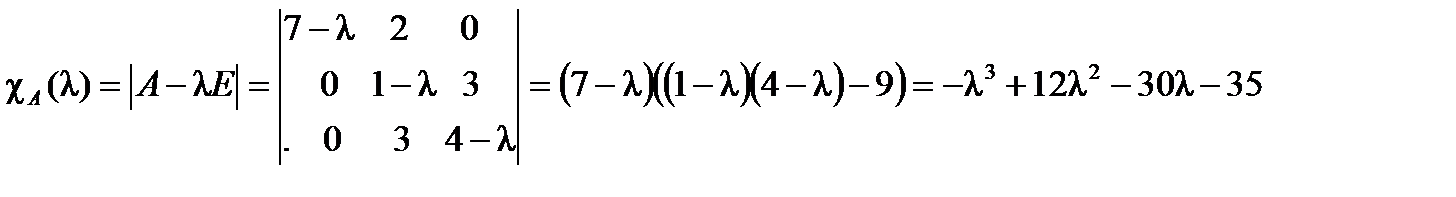 .
.
Квадратную матрицу можно использовать в качестве значения переменного в произвольном многочлене. Тогда значением многочлена от матрицы будет матрица того же порядка, что и исходная.
Пусть дана l-матрица  . Для каждого элементарного преобразования данной матрицы существует обратное преобразование, которое также будет элементарным.
. Для каждого элементарного преобразования данной матрицы существует обратное преобразование, которое также будет элементарным.
Определение. Канонической l-матрицей называется l-матрица, обладающая следующими свойствами:
1. Эта матрица диагональная, т. е. имеет вид 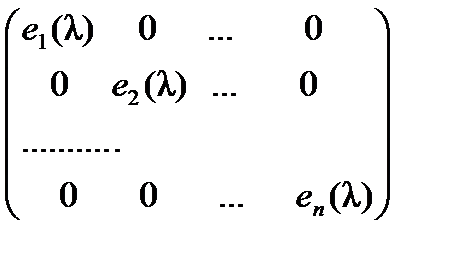 .
.
2. Всякий многочлен 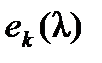 , 1 ≤ k ≤ n, нацело делится на многочлен
, 1 ≤ k ≤ n, нацело делится на многочлен 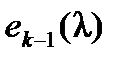 .
.
3. Старший коэффициент каждого многочлена равен 1, если этот многочлен отличен от нуля.
Если среди многочленов, стоящих на главной диагонали канонической матрицы, встречаются равные нулю, то они на главной диагонали занимают последние места. Многочлены нулевой степени занимают первые места.
К числу канонических l-матриц относятся, например, нулевая и единичная.
Любая l-матрица путем элементарных преобразований приводится к каноническому виду, т. е. всякая l-матрица эквивалентна некоторой канонической l-матрице.
Рассмотрим произвольную матрицу 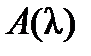 порядка п. Зафиксируем некоторое натуральное число k, 1 ≤ k ≤ n и рассмотрим все миноры k -го порядка матрицы. Вычисляя эти миноры, получим конечную систему многочленов от l; наибольший общий делитель этой системы многочленов, взятый со старшим коэффициентом 1, обозначим
порядка п. Зафиксируем некоторое натуральное число k, 1 ≤ k ≤ n и рассмотрим все миноры k -го порядка матрицы. Вычисляя эти миноры, получим конечную систему многочленов от l; наибольший общий делитель этой системы многочленов, взятый со старшим коэффициентом 1, обозначим 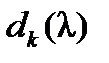 . Все многочлены, входящие в эту систему, однозначно определяются матрицей А. При этом
. Все многочлены, входящие в эту систему, однозначно определяются матрицей А. При этом 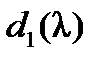 есть наибольший общий делитель всех элементов матрицы, взятый с коэффициентом 1.
есть наибольший общий делитель всех элементов матрицы, взятый с коэффициентом 1.
|
|
|
Наибольший общий делитель 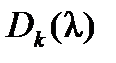 всех миноров k -го порядка матрицы
всех миноров k -го порядка матрицы 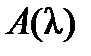 не меняется при выполнении в матрице
не меняется при выполнении в матрице 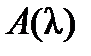 элементарных преобразований.
элементарных преобразований.
Рассмотрим матрицу 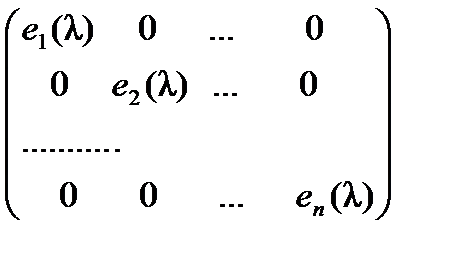 , эквивалентную матрице
, эквивалентную матрице 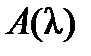 . Вычислим многочлен
. Вычислим многочлен 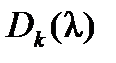 . Этот минор, стоящий в левом верхнем углу, равен
. Этот минор, стоящий в левом верхнем углу, равен 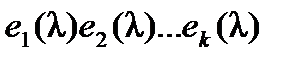 . Если минор k -го порядка содержит первую строку, то он делится на
. Если минор k -го порядка содержит первую строку, то он делится на 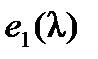 , так как он либо содержит множитель
, так как он либо содержит множитель 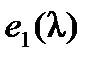 , либо равен нулю. Если минор k -го порядка на содержит первую строку, а содержит вторую, то он делится на
, либо равен нулю. Если минор k -го порядка на содержит первую строку, а содержит вторую, то он делится на 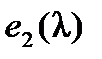 , а соответственно и на
, а соответственно и на 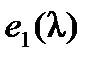 . Поэтому все миноры k -го порядка делятся на
. Поэтому все миноры k -го порядка делятся на 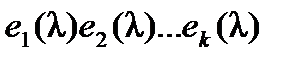 , т. е. это выражение является наибольшим общим делителем для всех миноров k -го порядка. Таким образом,
, т. е. это выражение является наибольшим общим делителем для всех миноров k -го порядка. Таким образом,
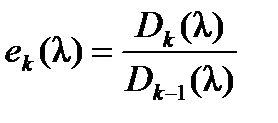 . (5.1)
. (5.1)
Определение. Аннулирующими многочленами называются многочлены, значения которых от данной матрицы есть нулевые матрицы.
В этом случае многочлен является аннулируемым данной матрицей А.
Определение. Многочлен наименьшей степени со старшим коэффициентом, равным единице, аннулируемый матрицей А, называется минимальным многочленом этой матрицы.
Теорема. Всякий многочлен f (l), аннулируемый матрицей А, делится на минимальный многочлен j(l) этой матрицы.
Доказательство. Если 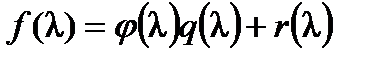 , где степень
, где степень 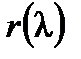 меньше степени
меньше степени 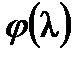 , то
, то 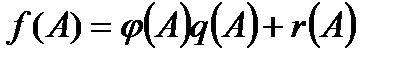 и из условия
и из условия 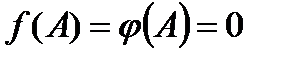 следует
следует 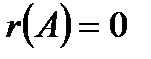 , что противоречит определению минимального многочлена. Теорема доказана.
, что противоречит определению минимального многочлена. Теорема доказана.
Теорема. Минимальный многочлен 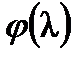 матрицы и ее характеристический многочлен
матрицы и ее характеристический многочлен 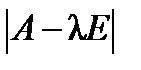 связаны соотношением
связаны соотношением
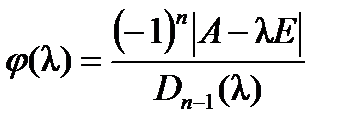 , (5.2)
, (5.2)
где 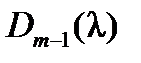 ˗ наибольший общий делитель всех миноров (п -1)-го порядка матрицы
˗ наибольший общий делитель всех миноров (п -1)-го порядка матрицы 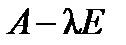 .
.
Доказательство. Следует из определения минимального и характеристического многочленов и формулы (5.1)
|
|
|
Пример 1. Найти минимальный многочлен матрицы 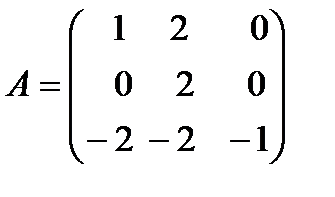 .
.
Решение. Найдем характеристический многочлен матрицы А: 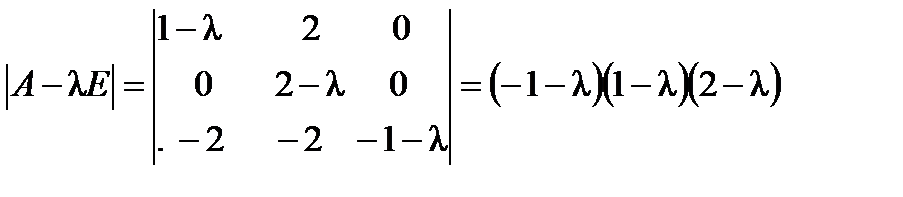 . Рассмотрим миноры второго порядка матрицы
. Рассмотрим миноры второго порядка матрицы 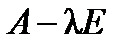 :
: 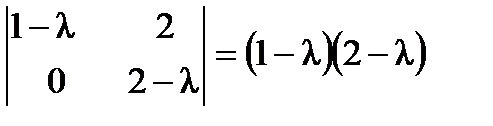 ,
, 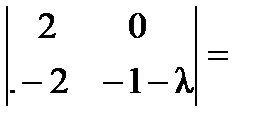
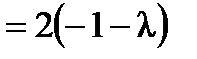 ,
, 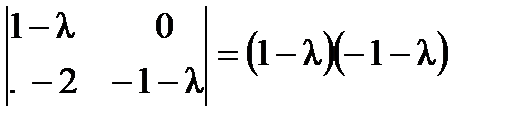 ,
, 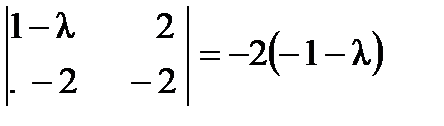 ,
, 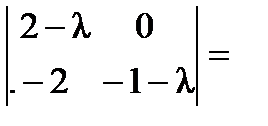
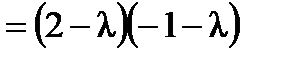 ,
, 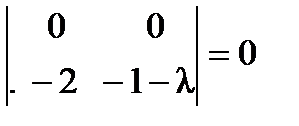 ,
, 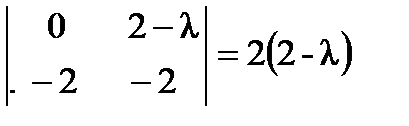 . Все остальные миноры равны нулю. Ненулевые миноры являются взаимно простыми, поэтому наибольший общий делитель всех миноров второго порядка матрицы
. Все остальные миноры равны нулю. Ненулевые миноры являются взаимно простыми, поэтому наибольший общий делитель всех миноров второго порядка матрицы 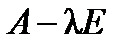 равен единице. Поэтому
равен единице. Поэтому  .
.
Пример 2. Найти минимальные многочлены матриц 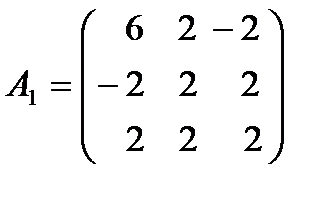 и
и 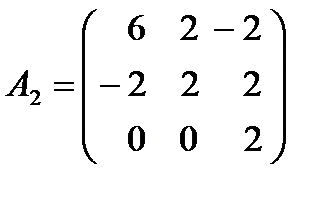 .
.
Решение. Составим характеристический многочлен матрицы 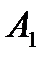 :
: 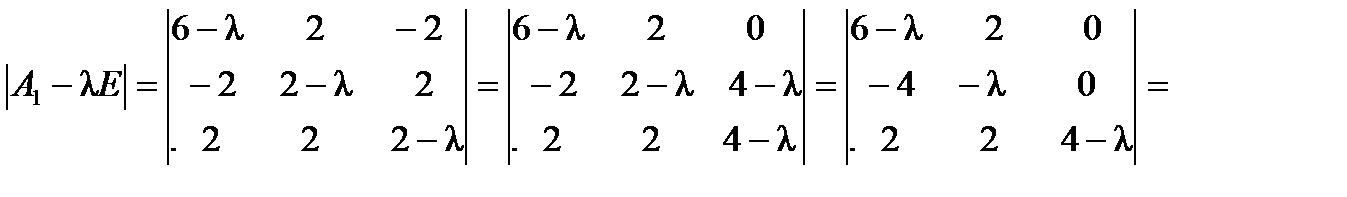
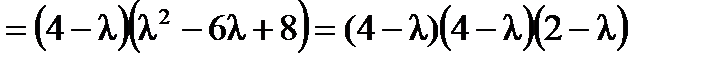 . Вычислим все миноры второго порядка:
. Вычислим все миноры второго порядка:
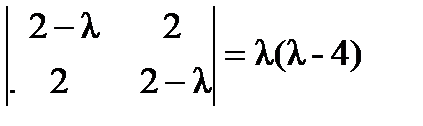 ;
; 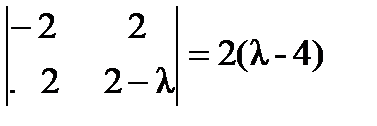 ;
; 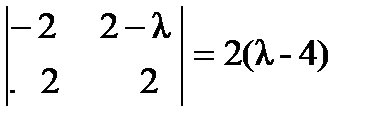 ;
;
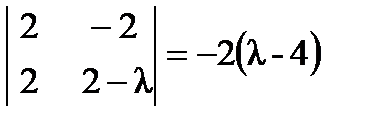 ;
; 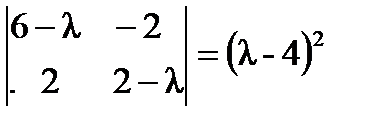 ;
; 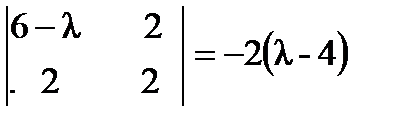 ;
;
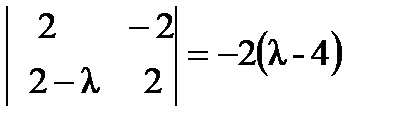 ;
; 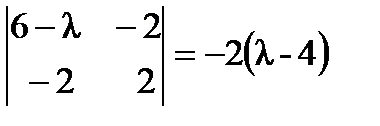 ;
; 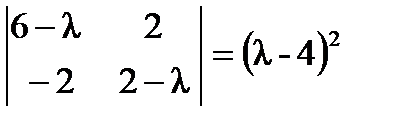 .
.
Для всех этих миноров 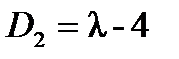 , поэтому минимальный многочлен матрицы
, поэтому минимальный многочлен матрицы 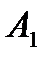 :
: 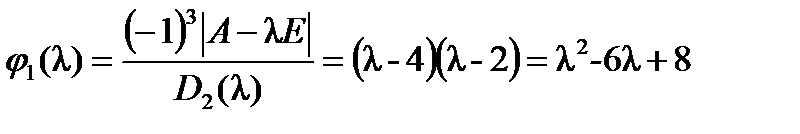 .
.
Для матрицы 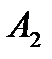 непосредственным вычислением найдем характеристический многочлен
непосредственным вычислением найдем характеристический многочлен 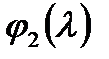 :
:
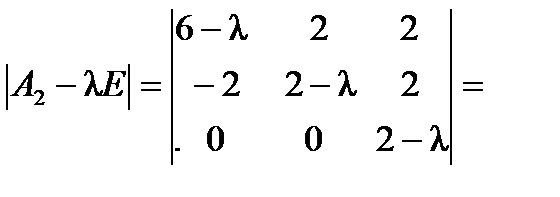
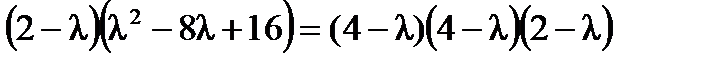 . Вычислим все миноры второго порядка:
. Вычислим все миноры второго порядка:
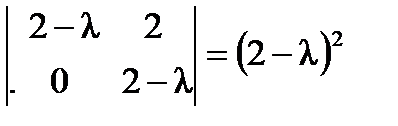 ,
, 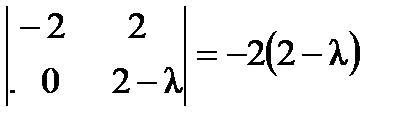 ,
, 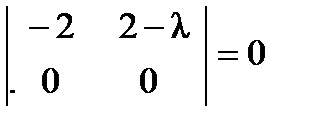 ,
, 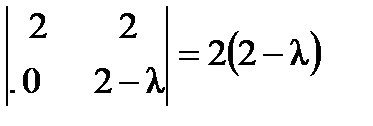 ,
, 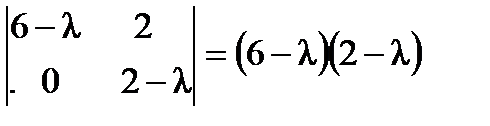 ,
, 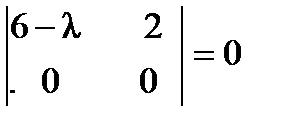 ,,
,, 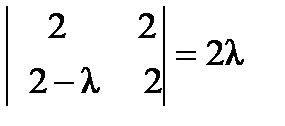 ,
, 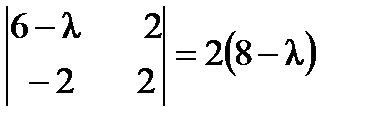 ,
, 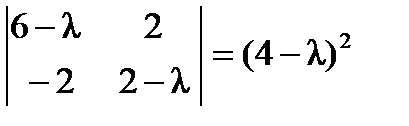 .
.
Первый и последний из этих миноров являются взаимно простыми, поэтому 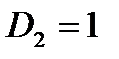 и
и 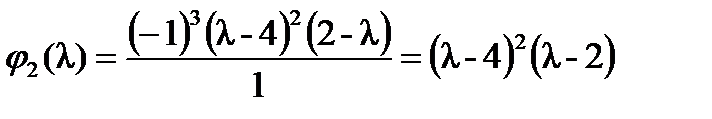 .
.
Теорема Кэли ˗ Гамильтона. Для любой квадратной матрицы характеристический многочлен является ее аннулирующим многочленом.
Теорема. Характеристические многочлены (уравнения) подобных матриц совпадают.
Доказательство. Пусть квадратные матрицы 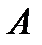 и
и  одного порядка подобны. Тогда существует невырожденная матрица
одного порядка подобны. Тогда существует невырожденная матрица 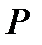 такая, что
такая, что 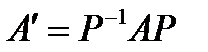 . Следовательно,
. Следовательно,
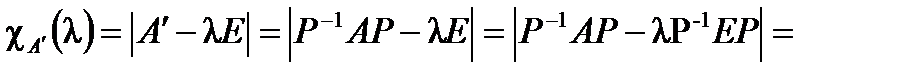
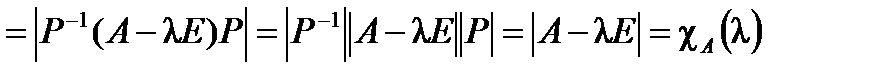 .
.
Теорема доказана.
|
|
|


