 |
векторов линейного оператора
|
|
|
|
Характеристическое уравнение линейного оператора  является алгебраическим уравнением п - й степени с действительными коэффициентами. Комплексные корни этого уравнения не относятся к собственным значениям линейного оператора, так как собственное значение - вещественное число по определению.
является алгебраическим уравнением п - й степени с действительными коэффициентами. Комплексные корни этого уравнения не относятся к собственным значениям линейного оператора, так как собственное значение - вещественное число по определению.
Вычисление собственных значений линейного оператора и его собственных векторов осуществляется в следующем порядке.
1. Выбрать в линейном пространстве некоторый базис и сопоставить оператору  матрицу
матрицу  этого линейного оператора в выбранном базисе.
этого линейного оператора в выбранном базисе.
2. Составить характеристическое уравнение  и найти все его действительные корни
и найти все его действительные корни  , которые будут собственными значениями оператора.
, которые будут собственными значениями оператора.
3. Для каждого собственного значения  найти фундаментальную систему решений для системы линейных однородных уравнений
найти фундаментальную систему решений для системы линейных однородных уравнений  . Столбцы фундаментальной системы решений представляют собой координаты векторов некоторого базиса в собственном подпространстве
. Столбцы фундаментальной системы решений представляют собой координаты векторов некоторого базиса в собственном подпространстве 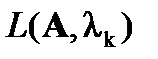 линейного оператора
линейного оператора 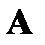 . Эти векторы будут собственными векторами, соответствующими собственному значению
. Эти векторы будут собственными векторами, соответствующими собственному значению  .
.
П р и м е р. Найти собственные значения и собственные векторы линейного оператора 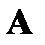 , имеющего в некотором базисе матрицу
, имеющего в некотором базисе матрицу 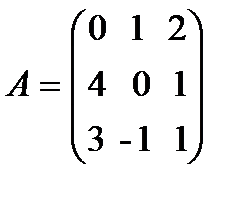 .
.
Решение. 1. Оператор уже представлен своей матрицей в некотором базисе.
2. Найдем собственные значения линейного оператора, решив характеристическое уравнение 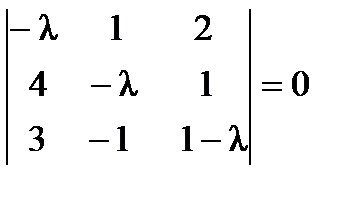 или
или 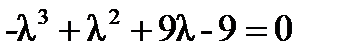 . Это уравнение имеет три вещественных корня
. Это уравнение имеет три вещественных корня  ,
,  ,
,  , которые и будут собственными значениями заданного линейного оператора.
, которые и будут собственными значениями заданного линейного оператора.
3. Для каждого собственного значения найдем собственные векторы. Столбцы координат собственных векторов являются решениями системы линейных однородных уравнений 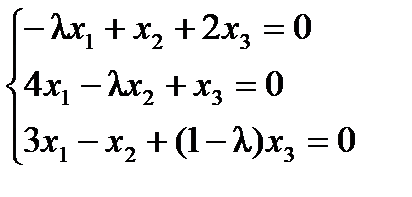 . Для
. Для  система уравнений имеет вид
система уравнений имеет вид  . Ранг матрицы этой системы равен 2, поэтому фундаментальная система содержит одно решение, например
. Ранг матрицы этой системы равен 2, поэтому фундаментальная система содержит одно решение, например 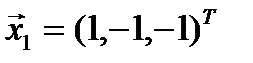 . Все множество собственных векторов линейного оператора с собственным значением
. Все множество собственных векторов линейного оператора с собственным значением  в координатной форме имеет вид
в координатной форме имеет вид  . Для
. Для  получаем систему уравнений
получаем систему уравнений  , ранг матрицы которой равен 2. Одним из ее решений будет
, ранг матрицы которой равен 2. Одним из ее решений будет 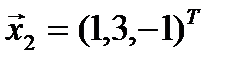 , поэтому все множество собственных векторов линейного оператора с собственным значением
, поэтому все множество собственных векторов линейного оператора с собственным значением  в координатной форме имеет вид
в координатной форме имеет вид  . Одним из решений системы уравнений для
. Одним из решений системы уравнений для 
 будет вектор
будет вектор  . Так как фундаментальная система содержит только одно решение, то все множество собственных векторов линейного оператора с собственным значением
. Так как фундаментальная система содержит только одно решение, то все множество собственных векторов линейного оператора с собственным значением  в координатной форме имеет вид
в координатной форме имеет вид 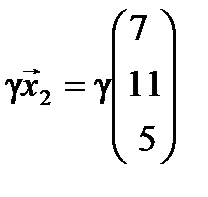 .
.
|
|
|
Определение. Матрица называется ортогональной, если ее обратная совпадает с транспонированной.
Определение. Вещественная строка называется нормированной, если сумма квадратов ее элементов равна единице.
Определение. Строки матрицы называются ортогональными, если сумма произведений соответствующих элементов равна нулю.
Ортогональность матрицы равносильна тому, что ее строки нормированы и попарно ортогональны. Из ортогональности матрицы следует ортогональность транспонированной с ней матрицы и обратно; а из нормированности и попарной ортогональности ее строк следует нормированность и ортогональность ее столбцов.
Свойства ортогональных матриц:
1. Если матрица ортогональна, то и обратная к ней ортогональна.
2. Произведение ортогональных матриц есть ортогональная матрица.
3. Единичная матрица ортогональна.
4. Определитель ортогональной матрицы равен ±1.
Ортогональные матрицы разбиваются на два класса – собственно ортогональные с определителем 1 и не собственно ортогональные с определителем ˗1.
Определение. Линейное преобразование φ евклидова пространства называется ортогональным, если оно сохраняет скалярный квадрат любого вектора, т. е. 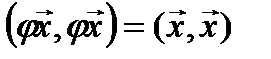 . Другими словами, ортогональное преобразование евклидова пространства сохраняет скалярное произведение любых двух векторов.
. Другими словами, ортогональное преобразование евклидова пространства сохраняет скалярное произведение любых двух векторов.
|
|
|
При ортогональном преобразовании евклидова пространства образы всех векторов любого ортонормированного базиса сами составляют ортонормированный базис.
Верно и обратное: если линейное преобразование евклидова пространства переводит хотя бы один ортонормированный базис в ортонормированный, то это преобразование ортогонально.
Ортогональное преобразование евклидова пространства в любом ортонормированном базисе задается ортогональной матрицей. Если же линейное преобразование евклидова пространства хотя бы в одном ортонормированным базисе задается ортогональной матрицей, то это преобразование ортогонально.
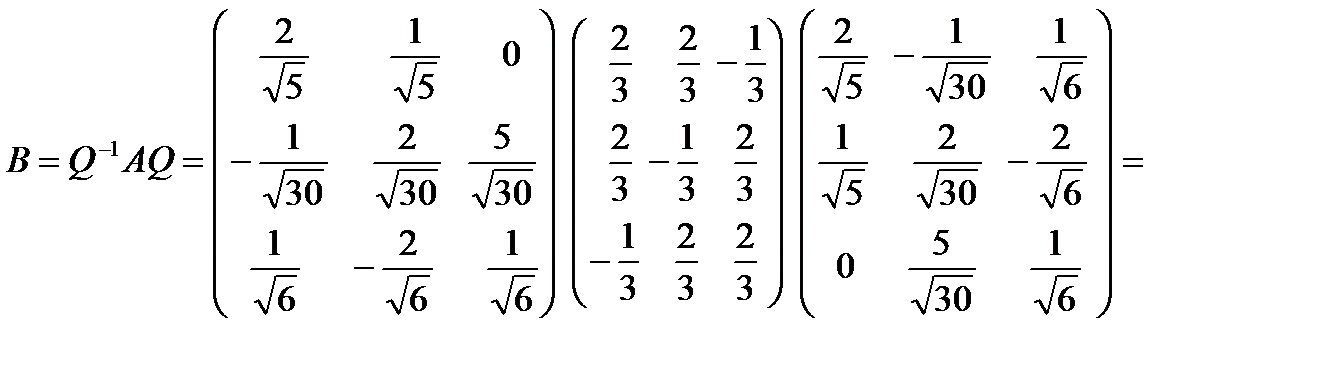
Пример. Для ортогонального преобразования  , заданного в ортонормированном базисе матрицей
, заданного в ортонормированном базисе матрицей  , найти ортонормированный базис, в котором матрица
, найти ортонормированный базис, в котором матрица  этого преобразования имеет канонический вид. Найти канонический вид. (Искомый базис определен неоднозначно.)
этого преобразования имеет канонический вид. Найти канонический вид. (Искомый базис определен неоднозначно.)  .
.
Решение. Составим характеристическое уравнение:  .
. 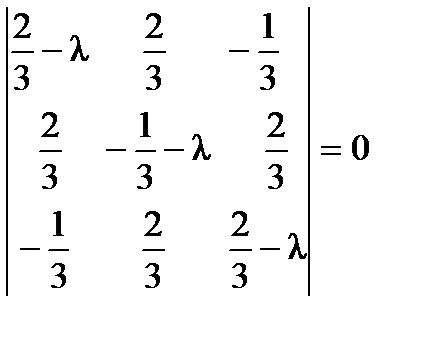 ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  .
.
Это уравнение имеет корни  .
.  , которые являются собственными значениями матрицы
, которые являются собственными значениями матрицы  . Найдем собственные векторы. Для
. Найдем собственные векторы. Для 
 ~
~  . Вектор
. Вектор  является собственным вектором. Второй собственный вектор
является собственным вектором. Второй собственный вектор  должен быть ортогональным вектору
должен быть ортогональным вектору  , поэтому его координаты удовлетворяют системе уравнений
, поэтому его координаты удовлетворяют системе уравнений 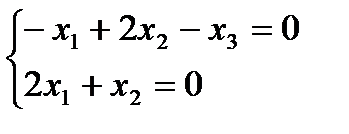 . Один из таких ˗ вектор
. Один из таких ˗ вектор  . Собственному значению
. Собственному значению  соответствует собственный вектор
соответствует собственный вектор  , который должен быть ортогонален векторам
, который должен быть ортогонален векторам  и
и  , поэтому
, поэтому  .
.
Искомый ортонормированный базис ˗ тот, в котором матрица имеет канонический вид, состоит из векторов 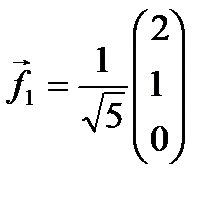 ,
, 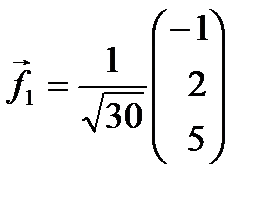 ,
,  , поэтому ортогональная матрица
, поэтому ортогональная матрица  ,
, 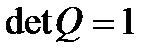 ,
,  .
.
Канонический вид матрицы:

 .
.
Пример. Найти ортонормированный базис собственных векторов и матрицу  в этом базисе для линейного преобразования, заданного в некотором ортонормированном базисе матрицей
в этом базисе для линейного преобразования, заданного в некотором ортонормированном базисе матрицей  (искомый базис определен неоднозначно):
(искомый базис определен неоднозначно):  .
.
Решение. Найдем собственные значения матрицы  . Составим характеристическое уравнение:
. Составим характеристическое уравнение:  ,
, 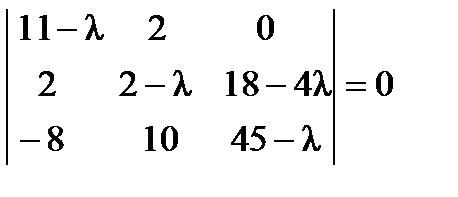 ,
, 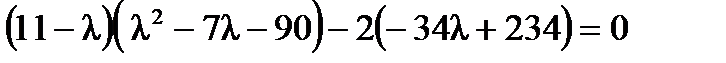 ,
,  ,
,  . Это уравнение имеет три корня
. Это уравнение имеет три корня  ,
,  ,
,  , которые являются собственными значениями матрицы
, которые являются собственными значениями матрицы  . Найдем собственные векторы. Для
. Найдем собственные векторы. Для  :
:  ~
~  ~
~ 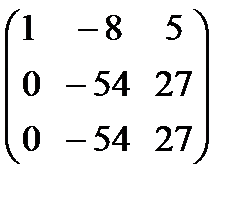 ~
~
~  , поэтому собственным вектором будет
, поэтому собственным вектором будет  . Для
. Для  :
: 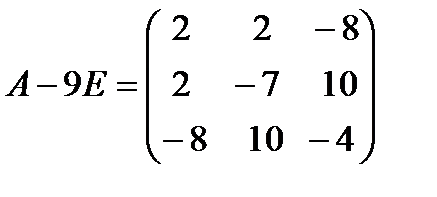 ~
~  ~
~ 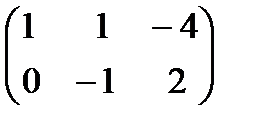 , поэтому собственным вектором будет
, поэтому собственным вектором будет  . Для
. Для  :
:  ~
~  ~
~  , поэтому собственным вектором будет
, поэтому собственным вектором будет 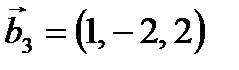 . Ортонормированный базис собственных векторов:
. Ортонормированный базис собственных векторов:  ,
,  ,
,  .
.  ,
,  ,
,  . Тогда искомая матрица вид
. Тогда искомая матрица вид  ,
,  .
.
|
|
|
5.6. Инвариантные подпространства
Определение. Подпространство 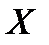 линейного пространства
линейного пространства  называется инвариантным относительно оператора
называется инвариантным относительно оператора 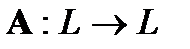 , если
, если 
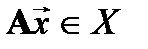 .
.
Любой линейный оператор имеет, как минимум, два тривиальных инвариантных подпространства - нулевое подпространство и все линейное пространство. К нетривиальным подпространствам относятся, например, собственные подпространства. Так как в комплексном линейном пространстве любой оператор имеет хотя бы один собственный вектор, то в таком пространстве любой оператор обязательно имеет хотя бы одно нетривиальное инвариантное подпространство.
Для любого оператора  образ
образ 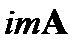 и ядро
и ядро 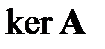 будут инвариантными подпространствами. Эти подпространства являются нетривиальными тогда и только тогда, когда оператор
будут инвариантными подпространствами. Эти подпространства являются нетривиальными тогда и только тогда, когда оператор  невырожденный или нулевой.
невырожденный или нулевой.
Если  - инвариантное подпространство, то можно различными способами построить дополнительное подпространство
- инвариантное подпространство, то можно различными способами построить дополнительное подпространство  такое, что
такое, что 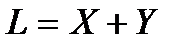 . Если среди таких дополнительных подпространств будет хотя бы одно инвариантное, то можно говорить о разложении линейного пространства
. Если среди таких дополнительных подпространств будет хотя бы одно инвариантное, то можно говорить о разложении линейного пространства  в прямую сумму подпространств
в прямую сумму подпространств  и
и  .
.
Разложение линейного пространства в прямую сумму инвариантных подпространств позволяет построить базис, в котором матрица линейного оператора имеет более простой вид.
Приведение матрицы линейного оператора к простому виду связано со структурой его инвариантных подпространств.
Если линейный оператор имеет базис из собственных векторов, то его матрица в некотором базисе является диагональной. Это верно, в частности, в том случае, когда все корни характеристического уравнения линейного оператора действительны и различны.
Теорема. Пусть  и
и  - инвариантные подпространства линейного оператора
- инвариантные подпространства линейного оператора  , причем
, причем  . Тогда в некотором базисе
. Тогда в некотором базисе 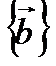 матрица А этого оператора имеет блочно-диагональный вид:
матрица А этого оператора имеет блочно-диагональный вид:
 , (5.7)
, (5.7)
где  и
и  - квадратные блоки порядка
- квадратные блоки порядка  и
и  соответственно, а 0 - нулевые блоки соответствующего типа.
соответственно, а 0 - нулевые блоки соответствующего типа.
|
|
|
Доказательство. Выберем в линейных подпространствах  и
и  базисы
базисы  и
и  . В совокупности эти базисы дадут базис
. В совокупности эти базисы дадут базис  всего линейного пространства
всего линейного пространства  . Так как
. Так как  ˗ инвариантное подпространство линейного оператора
˗ инвариантное подпространство линейного оператора  , то вектор
, то вектор  (
(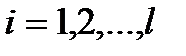 ) принадлежит
) принадлежит  и является линейной комбинацией векторов
и является линейной комбинацией векторов  . Поэтому координаты вектора
. Поэтому координаты вектора  , соответствующие векторам
, соответствующие векторам  (
( ) в базисе
) в базисе  , равны нулю. Аналогично можно показать, что координаты вектора
, равны нулю. Аналогично можно показать, что координаты вектора  , соответствующие векторам
, соответствующие векторам  (
(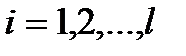 ) в базисе
) в базисе  , равны нулю. Таким образом, в базисе
, равны нулю. Таким образом, в базисе  линейного пространства
линейного пространства  матрица линейного оператора
матрица линейного оператора  имеет указанный вид. Теорема доказана.
имеет указанный вид. Теорема доказана.
Следствие. Если  - инвариантные подпространства линейного оператора
- инвариантные подпространства линейного оператора  , причем
, причем  , то в некотором базисе
, то в некотором базисе 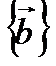 матрица А этого оператора имеет блочно-диагональный вид:
матрица А этого оператора имеет блочно-диагональный вид:
 , (5.8)
, (5.8)
где  - квадратные блоки порядка
- квадратные блоки порядка  ,
,  , …,
, …,  соответственно, а все остальные блоки являются нулевыми соответствующего типа.
соответственно, а все остальные блоки являются нулевыми соответствующего типа.
Доказательство аналогично доказательству теоремы.
Рассмотрим действие линейного оператора  только на векторах инвариантного подпространства
только на векторах инвариантного подпространства  . Если
. Если  , то
, то  , поэтому можно считать, что оператор
, поэтому можно считать, что оператор  порождает на подпространстве
порождает на подпространстве  некоторый другой оператор
некоторый другой оператор  ,
, 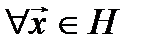 .
.
Оператор 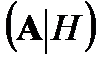 называется индуцированным оператором, порожденным оператором
называется индуцированным оператором, порожденным оператором  . По отношению к оператору
. По отношению к оператору 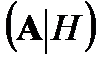 оператор
оператор  называется порождающим. В силу линейности оператора
называется порождающим. В силу линейности оператора  оператор
оператор 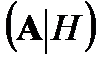 также будет линейным:
также будет линейным:
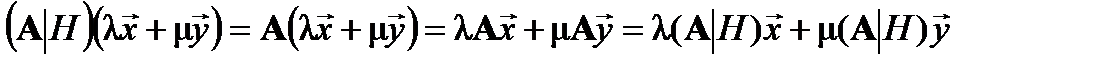 .
.
Индуцированный оператор 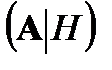 совпадает с порождающим оператором
совпадает с порождающим оператором 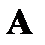 на инвариантном подпространстве
на инвариантном подпространстве  и не определен вне его, т. е. операторы
и не определен вне его, т. е. операторы 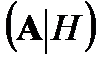 и
и  отличаются областью определения.
отличаются областью определения.
Так как индуцированный оператор 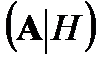 совпадает с порождающим оператором
совпадает с порождающим оператором  в инвариантном подпространстве, то из этого следует, что любой линейный оператор в каждом инвариантном подпространстве имеет хотя бы один собственный вектор.
в инвариантном подпространстве, то из этого следует, что любой линейный оператор в каждом инвариантном подпространстве имеет хотя бы один собственный вектор.
Если пространство разложено в прямую сумму  инвариантных подпространств, то линейный оператор
инвариантных подпространств, то линейный оператор  имеет по крайней мере
имеет по крайней мере  собственных векторов.
собственных векторов.
Любое собственное значение и любой собственный вектор индуцированного оператора являются собственным значением и собственным вектором порождающего оператора.
Теорема. Характеристический многочлен индуцированного оператора, порожденного на нетривиальном подпространстве, является делителем характеристического многочлена порождающего оператора.
Доказательство. Пусть индуцированный оператор 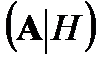 определен на инвариантном подпространстве
определен на инвариантном подпространстве  . Выберем в
. Выберем в  базис
базис  таким образом, чтобы векторы
таким образом, чтобы векторы  образовывали базис в
образовывали базис в  . Если
. Если  - матрица порождающего оператора, то
- матрица порождающего оператора, то  - матрица индуцированного оператора. Характеристический многочлен для оператора
- матрица индуцированного оператора. Характеристический многочлен для оператора  равен
равен 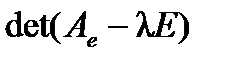 , для
, для 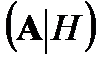 характеристический многочлен равен
характеристический многочлен равен  . Разложим
. Разложим  по первым
по первым  столбцам:
столбцам:
|
|
|
 , т. е. характеристический многочлен индуцированного оператора является делителем характеристического многочлена порождающего оператора. Теорема доказана.
, т. е. характеристический многочлен индуцированного оператора является делителем характеристического многочлена порождающего оператора. Теорема доказана.
Теорема. Любой линейный оператор  , действующий в п -мерном комплексном пространстве, имеет по крайней мере одно инвариантное подпространство размерности
, действующий в п -мерном комплексном пространстве, имеет по крайней мере одно инвариантное подпространство размерности  .
.
Доказательство. Оператор  имеет хотя бы один собственный вектор
имеет хотя бы один собственный вектор  . Пусть этот вектор соответствует собственному значению
. Пусть этот вектор соответствует собственному значению  . Тогда область значений
. Тогда область значений 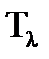 оператора
оператора  представляет собой инвариантное подпространство оператора
представляет собой инвариантное подпространство оператора  . Так как оператор
. Так как оператор  невырожденный, то подпространство
невырожденный, то подпространство 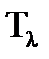 имеет размерность не выше
имеет размерность не выше  . Рассмотрим произвольное подпространство
. Рассмотрим произвольное подпространство  размерности
размерности  , содержащее подпространство
, содержащее подпространство  . Для любого вектора
. Для любого вектора 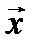 из
из 
 , следовательно, любой вектор их линейного подпространства
, следовательно, любой вектор их линейного подпространства  переходит в вектор этого подпространства. Поэтому
переходит в вектор этого подпространства. Поэтому  является инвариантным относительно оператора
является инвариантным относительно оператора  и соответственно относительно оператора
и соответственно относительно оператора  . Теорема доказана.
. Теорема доказана.
5.7 Треугольная форма
Теорема. Для любого линейного оператора  ,
,  , существуют инвариантные подпространства
, существуют инвариантные подпространства  размерности
размерности  (
( ) такие, что
) такие, что 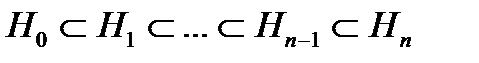 .
.
Доказательство. Существование линейных подпространств  и
и  очевидно. Согласно доказанной ранее теореме оператор
очевидно. Согласно доказанной ранее теореме оператор  имеет инвариантное подпространство
имеет инвариантное подпространство  .
.
Рассмотрим на подпространстве  индуцированный оператор. Как и любой оператор, заданный на
индуцированный оператор. Как и любой оператор, заданный на  , он имеет инвариантное подпространство
, он имеет инвариантное подпространство  . Но подпространство, инвариантное для индуцированного оператора, будет инвариантным и для порождающего оператора
. Но подпространство, инвариантное для индуцированного оператора, будет инвариантным и для порождающего оператора  . Следовательно, доказано существование инвариантного подпространства
. Следовательно, доказано существование инвариантного подпространства  . Если рассматривать индуцированный оператор на подпространстве
. Если рассматривать индуцированный оператор на подпространстве  , то аналогично доказывается существование инвариантного подпространства
, то аналогично доказывается существование инвариантного подпространства 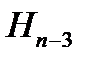 и т. д. Теорема доказана.
и т. д. Теорема доказана.
Построим базис 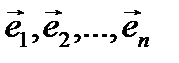 в линейном пространстве
в линейном пространстве  , используя инвариантные подпространства
, используя инвариантные подпространства  ,
,  . В качестве вектора
. В качестве вектора  возьмем любой ненулевой вектор из
возьмем любой ненулевой вектор из  , в качестве
, в качестве  - произвольный ненулевой вектор из
- произвольный ненулевой вектор из  , не принадлежащий
, не принадлежащий  и т. д. Рассмотрим матрицу
и т. д. Рассмотрим матрицу 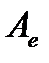 оператора
оператора 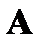 в этом базисе. Так как вектор
в этом базисе. Так как вектор 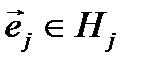 , а подпространство
, а подпространство  инвариантно относительно оператора
инвариантно относительно оператора 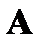 , то вектор
, то вектор 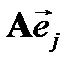 должен быть линейной комбинацией только векторов
должен быть линейной комбинацией только векторов  . Поэтому в разложении
. Поэтому в разложении  коэффициенты
коэффициенты  , т. е. матрица оператора имеет вид
, т. е. матрица оператора имеет вид 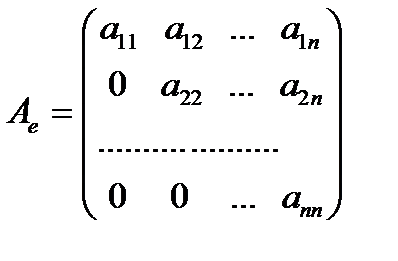 , где
, где  при
при  ,
,  ,
,  .
.
Если оператор 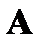 имеет в некотором базисе треугольную матрицу
имеет в некотором базисе треугольную матрицу  , то ее диагональные элементы совпадают с собственными значениями оператора
, то ее диагональные элементы совпадают с собственными значениями оператора 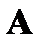 даже с учетом их кратности:
даже с учетом их кратности:  .
.
5.8. Линейные операторы простой структуры
Определение. Линейный оператор, действующий в линейном пространстве  , называется оператором простой структуры, если в пространстве
, называется оператором простой структуры, если в пространстве  существует базис, состоящий из собственных векторов этого оператора.
существует базис, состоящий из собственных векторов этого оператора.
В базисе из собственных векторов матрица оператора  простой структуры имеет вид:
простой структуры имеет вид:
 , (5.7)
, (5.7)
где  - собственные значения оператора.
- собственные значения оператора.
Если в исходном базисе  оператор простой структуры имеет матрицу
оператор простой структуры имеет матрицу 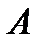 , а в базисе
, а в базисе  из собственных векторов - матрицу
из собственных векторов - матрицу  , то в силу соотношения (7.3) имеем:
, то в силу соотношения (7.3) имеем:
 , (5.8)
, (5.8)
где  - матрица перехода от базиса
- матрица перехода от базиса  к базису
к базису  . Она состоит из столбцов координат векторов базиса
. Она состоит из столбцов координат векторов базиса  в базисе
в базисе  ,
, 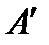 - матрица вида (8.5). Другими словами, матрица
- матрица вида (8.5). Другими словами, матрица  приводится матрицей
приводится матрицей  к диагональному виду.
к диагональному виду.
Определение. Замена матрицы  диагональной матрицей
диагональной матрицей  , подобной
, подобной  , называется приведением матрицы
, называется приведением матрицы  к диагональному виду.
к диагональному виду.
Разрешив соотношение (8.6) относительно матрицы  , получим
, получим
 . (5.9)
. (5.9)
Соотношение (8.7) называется каноническим разложением матрицы  .
.
При построении матрицы  нужно найти собственные значения матрицы
нужно найти собственные значения матрицы  и при каждом собственном значении
и при каждом собственном значении  построить ФСР (фундаментальную систему решений) однородной системы уравнений
построить ФСР (фундаментальную систему решений) однородной системы уравнений  . Из решений всех построенных ФСР, как из столбцов, составить матрицу
. Из решений всех построенных ФСР, как из столбцов, составить матрицу  . В матрице
. В матрице  столбцами записываются решения по каждому
столбцами записываются решения по каждому  в порядке нумерации собственных значений
в порядке нумерации собственных значений  (одинаковые
(одинаковые  считаются столько раз, каковы их кратности; все
считаются столько раз, каковы их кратности; все  можно перенумеровать так, что будет
можно перенумеровать так, что будет  ,
,  ).
).
Если матрица  окажется квадратной, то она будет удовлетворять соотношениям (8.6), (8.7). Если же матрица
окажется квадратной, то она будет удовлетворять соотношениям (8.6), (8.7). Если же матрица  будет прямоугольной, то выполнение соотношений (8.6), (8.7) невозможно, т. е. матрица
будет прямоугольной, то выполнение соотношений (8.6), (8.7) невозможно, т. е. матрица  не приводится к диагональному виду и не имеет канонического разложения.
не приводится к диагональному виду и не имеет канонического разложения.
Этот способ равносилен нахождению невырожденной матрицы 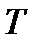 из матричного уравнения
из матричного уравнения  . Из способа построения матрицы
. Из способа построения матрицы  следует, что она будет квадратной лишь в случае, когда каждое характеристическое число матрицы
следует, что она будет квадратной лишь в случае, когда каждое характеристическое число матрицы 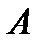 является ее собственным значением и для каждого
является ее собственным значением и для каждого  совпадает его алгебраическая кратность с геометрической кратностью, т. е. с максимальным числом линейно независимых векторов матрицы
совпадает его алгебраическая кратность с геометрической кратностью, т. е. с максимальным числом линейно независимых векторов матрицы  по
по  , равным
, равным  , где
, где  - ранг матрицы
- ранг матрицы  . Если оператор с матрицей
. Если оператор с матрицей  является оператором простой структуры, то матрица
является оператором простой структуры, то матрица  приводится к диагональному виду.
приводится к диагональному виду.
П р и м е р. Привести, если возможно, действительную матрицу  к диагональному виду и построить для нее каноническое разложение.
к диагональному виду и построить для нее каноническое разложение.
Решение. Найдем корни характеристического уравнения 
 . Ими являются числа
. Ими являются числа  ,
, 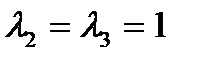 кратности 1 и 2 соответственно. Все они действительные, поэтому являются собственными значениями матрицы
кратности 1 и 2 соответственно. Все они действительные, поэтому являются собственными значениями матрицы  . При
. При  матрица
матрица 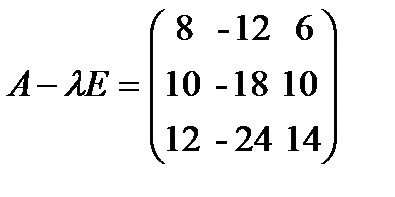 имеет ранг
имеет ранг  , поэтому
, поэтому 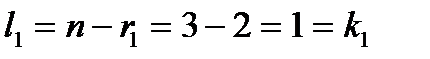 . При
. При 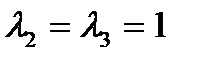 матрица
матрица  имеет ранг
имеет ранг  , поэтому
, поэтому 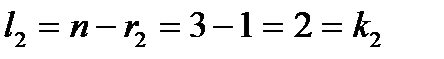 . Таким образом, у матрицы
. Таким образом, у матрицы  геометрическая кратность каждого
геометрическая кратность каждого  совпадает с его алгебраической кратностью, поэтому матрица
совпадает с его алгебраической кратностью, поэтому матрица  приводится к диагональному виду
приводится к диагональному виду  . В этом можно убедиться и непосредственным конструированием матрицы
. В этом можно убедиться и непосредственным конструированием матрицы  , удовлетворяющей соотношению (8.6). Действительно, при
, удовлетворяющей соотношению (8.6). Действительно, при  система
система  , т. е. система уравнений
, т. е. система уравнений 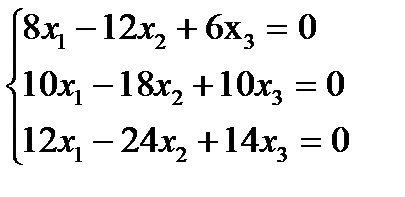 имеет общее решение
имеет общее решение  , в котором одно свободное неизвестное. Поэтому ФСР этой системы состоит из одного решения, например,
, в котором одно свободное неизвестное. Поэтому ФСР этой системы состоит из одного решения, например,  . При
. При  система
система  , т. е. система уравнений
, т. е. система уравнений  имеет общее решение
имеет общее решение  . Полагая в общем решении сначала
. Полагая в общем решении сначала  ,
,  , затем
, затем  ,
,  , соответственно получим частные решения
, соответственно получим частные решения 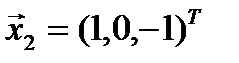 ,
, 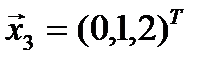 . Из решений
. Из решений  , как из столбцов, составляется невырожденная матрица
, как из столбцов, составляется невырожденная матрица 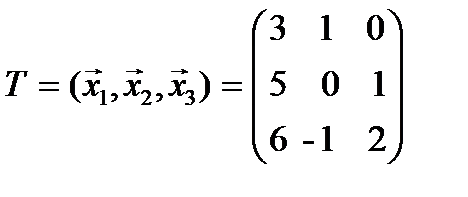 . Поэтому матрица
. Поэтому матрица  приводится к диагональному виду
приводится к диагональному виду  и имеет каноническое разложение
и имеет каноническое разложение 
 .
.
5.8. Жорданова форма.
Рассмотрим более подробно корневые подпространства. Если  , то
, то  . Но для каждого определенного вектора
. Но для каждого определенного вектора  возможно выполнение равенства
возможно выполнение равенства  при
при  . В частности, если
. В частности, если  - собственный вектор, соответствующий кратному собственному значению
- собственный вектор, соответствующий кратному собственному значению  ,
, 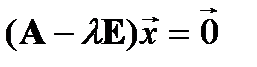 , хотя
, хотя 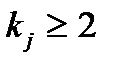 .
.
Определение. Высотой корневого вектора  называется наименьшее целое неотрицательное число
называется наименьшее целое неотрицательное число 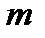 , для которого
, для которого 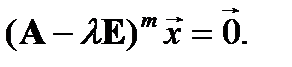
Все корневые векторы, соответствующие собственному значению  , имеют высоты, не превосходящие
, имеют высоты, не превосходящие  . В общем случае высоты корневых векторов и кратности собственных значений - два различных понятия. Для операторов простой структуры не существует корневых векторов высоты больше единицы независимо от кратности собственных значений.
. В общем случае высоты корневых векторов и кратности собственных значений - два различных понятия. Для операторов простой структуры не существует корневых векторов высоты больше единицы независимо от кратности собственных значений.
Пусть  - корневое подпространство, соответствующее собственному значению
- корневое подпространство, соответствующее собственному значению  кратности
кратности  . Обозначим через
. Обозначим через


