 |
Относительный покой жидкости
|
|
|
|
Относительным покоем жидкости называется случай её движения, при котором вся масса жидкости движется как твердое тело, отдельные
её части не смещаются одна относительно другой.
Рассмотрим два случая.
Случай первый. Сосуд с жидкостью движется прямолинейно
и равноускоренно (рис. 1.13).
Пусть сосуд движется с ускорением a. Сила инерции 
направлена в сторону, обратную ускорению, сила тяжести 
направлена вниз. Найдем направление и величину равнодействующей массовой силы:
(1.30)
где и – векторы единичных сил инерции и тяжести. Для всех частиц рассматриваемого объема жидкости равнодействующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны к этим силам, в том числе и свободная поверхность.
Рис. 1.13. Схема относительного покоя жидкости
Давление в любой точке определяется по формуле:
(1.31)
где 
– давление на свободной поверхности, j – единичная массовая сила, r – плотность жидкости, l – расстояние по нормали от точки до свободной поверхности. Если 
, то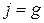 
, и уравнение (1.31) превратится
в основное уравнение гидростатики.
Случай второй. Сосуд равномерно вращается вокруг вертикальной оси с угловой скоростью 
(рис. 1.14).
В данном случае массовыми силами являются сила тяжести
и центробежная сила.
Воспользуемся основным дифференциальным уравнением гидростатики (1.3):
Рис. 1.14. Равновесие жидкости во вращающемся сосуде
Для решения задачи перейдем к цилиндрической системе координат r, j, z. Нетрудно доказать, что:
(1.32)
где 
– единичная центробежная (отнесенная к единице массы) сила. Тогда вместо (1.3) получим:
(1.33)
Запишем граничное условие: при 
Проинтегрировав (1.33) и воспользовавшись граничным условием, получим:
|
|
|
(1.34)
Уравнение (1.34) представляет собой закон распределения давления внутри жидкости в зависимости от координат r и z.
Выражение в скобках 
представляет собой глубину погружения рассматриваемой точки А под свободной поверхностью. Подставляя значение h в уравнение (1.34), получим:
(1.35)
Уравнение (1.35) совпадает с уравнением (1.7), записанным для покоящейся жидкости. Однако форма свободной поверхности, от которой отсчитывается глубина погружения для уравнения (1.35), иная. Как известно, на свободной поверхности 
. Тогда из уравнения (1.34) получим формулу свободной поверхности в виде:
. (1.36)
В уравнении (1.36) z является текущей координатой свободной поверхности.
Уравнение (1.36) описывает кривую в виде параболы, а свободная поверхность, полученная на основе этой кривой, является параболоидом вращения.
На практике чаще всего встречаются случаи, когда 
. Тогда поверхности уровня жидкости без большой ошибки можно считать круглыми цилиндрами с общей осью – осью вращения сосуда. Тогда
для давления получим выражение:
(1.37)
где 
– внутренний радиус ротора, 
– радиус свободной поверхности жидкости.
Контрольные вопросы
1. Что называется давлением? Какова размерность давления
в различных системах единиц и каковы соотношения между ними?
2. Как определяется величина абсолютного, избыточного
и вакуумметрического давлений?
3. Какие существуют приборы для измерения давления и вакуума?
4. В чем смысл закона Паскаля? В каких случаях он используется
в технике?
5. В чем смысл гидростатического парадокса?
6. Что такое поверхность равного давления, каково её уравнение?
7. Отличается ли форма поверхностей равного давления при относительном покое жидкости в равномерно вращающемся относительно вертикальной оси цилиндрическом сосуде и в сосудах, движущихся прямолинейно равноускоренно или равнозамедленно?
8. Справедливо ли основное уравнение гидростатики в различных случаях относительного покоя?
|
|
|
9. В каком случае могут совпадать центр тяжести и центр давления для плоской поверхности?
10. Как определяются составляющие силы давления покоящейся жидкости на криволинейные поверхности? Каков смысл термина «объем жидкого тела»?
11. В чем физический смысл закона Архимеда?
12. Получите основное уравнение гидростатики, используя уравнение Бернулли.
13. Давление на свободной поверхности жидкости больше атмосферного. Как в этом случае определяется избыточное давление
в точке, находящейся на глубине h?
14. Почему точка приложения внешней силы 
и силы избыточного давления 
разные?
15. Почему при 
поверхность равного давления
в цилиндрическом сосуде практически совпадает c цилиндрической поверхностью?
ГИДРАВЛИКА
Первоначальное название «гидравлика» включало в себя только учение о движении воды по трубам. В настоящее время различие между гидравликой и прикладной гидромеханикой исчезает. Современная гидравлика довольно часто использует законы классической гидромеханики, например, уравнения Эйлера, Навье – Стокса, неразрывности и т.д. В то же время отличительной чертой гидравлики является доведение решений до конца, удобных для практических расчетов.
|
|
|
