Исследование зависимости давления насыщенного пара от температуры и определение удельной теплоты испарения бензола

Цель работы: экспериментально изучить зависимость давления насыщенного пара от температуры; определить удельную теплоту испарения бензола.

Теоретический материал: Понятие о фазе состояния вещества. Уравнение Ван-дер-Ваальса и его анализ. Физический смысл постоянных. Свойства насыщенного па­ра я существующей с ним жидкости, фазовые переходы первого и второ­го рода. Критические явления. Критическая температура. Уравнение Клайперона-Клаузиуса, вывод и физический смысл. Термодинамический потенциал. Вывод уравнения Клайперона-Клауэиуса из термодинамического потенциала. Метастабильные состояния. Кривые равновесия фаз в различных переменных. Кривая кипения. Тройная точка. Правило фаз. Изменение энтропии при фазовом переходе первого рода.

Для описания состояния вещества и происходящих в нём фазовых переходов удобнее всего пользоавться диаграммой состояний.

Рис. 1

Типичная диаграмма состояний изображена на рис. 1. Как видно из рисунка, обдасти существования различных фаз разграничены линиями ВА, АК, АД. Любая точка на этих линиях соответствует тем значениям давления и температуры, при которых вещество существует одновременно в виде двух фаз, находящихся в равновесии. Кривая АК дает связь между давлением и температурой, при которых жидкость находится в равновесии со своим паром. Точка К ─ критическая точка, в которой исчезает различие между жидкостью и паром. Кривая АВ изображает давления и температуры существования твердой и газообразной фаз, а кривая АД ─ твердой и жидкой. Только в так называемой тройной точке А одновременно существуют и находятся в равновесии все три фазы. При равновесии двух фаз равны их температуры и давления. Поэтому, если имеет место равновесный фазовый переход некоторой массы вещества, например жидкой фазы в газообразную, то этот процесс происходит при неизменных температуре и давлении, т.е. является изотермическим и изобарическим.

Если совершается равновесный фазовый переход из одного состояния в другое, то изменение энтропии системы равно , где 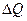─ теплота, подведенная к системе в течение процесса при температуре перехода . Согласно первому закону термодинамики, подводимая к системе теплота 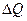, затрачивается на увеличение внутренней энергии системы и на работу расширения т.е.

или

Выражая приращение энтропии, внутренней энергии в объеме как разности соответствующих величин в этих состояниях последнее уравнение можно переписать в виде

или

Функция называется термодинамическим потенциалом. Последнее равенство означает, в частности, что термодинамический потенциал при фазовом превращении некоторой массы вещества в жидком состоянии равен термодинамическому потенциалу этой же массы в газообразном состоянии. Поскольку равновесное состояние определяется в результате противоборства двух тенденций ─ стремления энергии системы к минимуму и стремления её энтропии к максимуму, то из этого равенства следует, что состоянию равновесия соответствует минимум термодинамического потенциала.

Чтобы установить зависимость давления насыщенного пара от температуры возьмем на кривой фазового равновесия две точки и и запишем условия равновесия при фазовом переходе для этих точек.

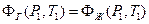и

Вычитая получим

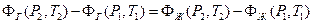
Если точки 1 и 2 выбраны достаточно близко друг к другу, то последнее равенство можно преобразовать с помощью формулы приращения функции двух переменных и записать

Из определения термодинамического потенциала следует, что

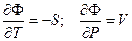
Подставляя эти значения производны в предыдущее уравнение, получим

или

Из этого уравнения получается зависимость давления насыщенного пара от температуры.

Так как , то

Запишем это выражение для фазового перехода единицы массы из жидкого в газообразное состояние

(1)

где 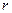─ удельная теплота испарения жидкости при температуре перехода ─ удельные объемы, т.е. объемы единицы массы в газообразном и жидком состоянии в точке фазового перехода. Эта формула называется уравнением Клайперона – Клаузиуса. Из приведенного вывода следует, что оно применимо к линии равновесия любых двух фаз. В общем случае 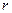─ удельная теплота перехода из одной фазы в другую, (теплота плавления на линии АД, теплота сублимации на линии ВА).

Уравнение Клайперона – Клаузиуса можно использовать для определения теплоты испарения жидкости. При температурах значительно ниже критической удельный объем жидкости значительно меньше удельного объема пара и им можно пренебречь в уравнении (1). Тогда

Кроме того, плотность насыщенного пара , очень мала и к газу можно применить уравнение состояния идеального газа

где ─ давление насыщенного пара, ─ масса моля. Из последнего уравнения . Подставив это значение 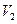в уравнение Клайперона – Клаузиуса, получим . Если принять, что теплота испарения 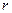не зависит от температуры, то, интегрируя последнее уравнение, получим 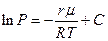. Или после перехода к десятичным логарифмам

(2)

На самом деле теплота испарения 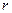является функцией температуры, однако, применяя уравнение к узкому интервалу температур, можно использовать среднее значение теплоты испарения.

Последнее уравнение показывает, что в нешироком интервале температур зависимость от на кривой испарения линейна. Тангенс угла наклона графика этой линии к оси равен

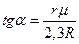
Таким образом, для определения среднего значения удельной теплоты испарения надо по экспериментальным значениям и построить график зависимости и из него определить тангенс угла наклона полученной прямой к оси , а затем рассчитать среднее значение теплоты испарения для исследуемого интервала температур по формуле

(3)

Рис. 2

Для получения зависимости от и определения удельной теплоты испарения в данной работе используется установка, схема которой приведена на рис. 2. В U – образную трубку залита ртуть, над которой в запаянном конце находится капля бензола, а над ней насыщенный пар. Второй конец U – образной трубки через буферный сосуд Д, манометр М, кран К соединен с насосом, позволяющим делать в системе необходимое разряжение. U – образная трубка помещается в стакан с водой, подогреваемый электроплиткой. Температуру воды, а следовательно и бензола, измеряют при помощи термометра Т. Давление насыщенных паров бензола измеряется манометром М, когда уровни ртути к коленах U – образной трубки уравновешиваются. Измеряя давление при различных температурах, т.е. уравновешивая уровни ртути и снимая показания манометра, получают искомую зависимость от .

Порядок выполнения работы.

1. Повернуть кран в такое положение, чтобы насос был соединен с U – образной трубкой. При комнатной температуре создать в системе разряжение. Откачку ведут до тех пор пока не уравновесятся уровни ртути в обоих коленах U – образной трубки. Манометром измерить давление паров бензола при комнатной температуре.

Примечание: для определения давления насыщенных паров бензола при комнатных и других температурах необходимо от 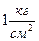вычесть показания манометра.

2. При помощи крана соединить систему с воздухом и включить нагреватель. При достижении 50°С внимательно следить за уровнем ртути в запаянном конце. Как только уровень начнет опускаться, выключить нагреватель. Откачивая воздух, определить давление, при котором уровни в обоих коленах уравняются для данной температуры.

3. Дальнейшие измерения давления делают по мере остывания через каждые 5 градусов. Данные и занести в таблицу

	Комнат t

 

4. По данным измерений построить два графика:

а) зависимость от ;

б) зависимость

По графику (б) найти и по формуле (3) расчищать удельную теплоту испарения бензола.

 

Контрольные вопросы:

1. Что называют фазой системы? Что такое фазовые переходы и фазовые равновесия? В чем заключается разница между фазовыми переходами первого и второго рода? Приведите примеры. Что называется теплотой фазового перехода? В каких единицах она измеряется?

2. Что называется насыщенным паром? Как изменяется давление насыщенного пара с изменением температуры? Изобразите на плоскости P,T кривую равновесия пара и жидкости. Где начинается и заканчивается эта кривая? Изобразите область равновесия жидкости и пара на плоскости P,V.

3. Какая температура называется критической? Что такое критическое состояние? Возможен ли непрерывный переход из газообразного состояния в жидкое, минуя стадию двухфазного состояния? Как его осуществить? Каким явлением сопровождается исчезновение двухфазного состояния жидкость-газ в критической точке? Можно ли перевести вещество из газообразного состояния в жидкое при температуре выше критической?

4. Что называется испарением? Почему испарение может происходить при любой температуре? Что такое удельная теплота испарения? От чего она зависит? Чему равна теплота испарения при критической температуре?

5. Что называется кипением? Чем кипение отличается от испарения? Как температура кипения зависит от внешнего давления? Можно ли, снимая кривую кипения, получить кривую равновесия жидкость-пар?

6. Жидкость переходит в пар той же температуры. Как при этом меняется удельный термодинамический потенциал, энтропия, внутренняя энергия?

7. Запишите уравнение Клайперона-Клаузиуса для однокомпонентной двухфазной системы. Какие величины связывают это уравнение. Примените уравнение Клайперона-Клаузиуса к процессу перехода жидкости в пар.

8. Получите функциональную зависимость давления насиненного пара от температуры. При каких допущениях выводится эта зависимость?

9. Как в данной работе получают экспериментальную кривую зависимости давления насыщенного пара бензола P от температуры T? Покажите, как на основании этой кривой рассчитать удельную теплоту испарения бензола?

 

Литература:

1. Методическое указание.

2. А.Н. Матвеев. Молекулярная физика. -М., Высшая школа, 1961, §32, 35, 41.

3. А.К. Кикоин, И.К. Кикоин. Молекулярная физика. -М., Наука, 1976, §62, 63, 65, 66, 67, 104, 107, 130-131.

 

 

Лабораторная работа № 13

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: