 |
Изучение статистических закономерностей случайных процессов
|
|
|
|
Целью данной работы есть ознакомление на практике со статистическими величинами и закономерностями, с помощью которых можно оценивать и обрабатывать данные измерения случайных величин.
В качестве примера статистического анализа распределения событий предлагается экспериментальные исследования распределения интенсивности космического излучения как случайного процесса. Под интенсивностью понимается число космических частичек, которая регистрируется счетчиком частичек в единицу времени.
Краткие теоретические сведения.
Пусть в течение некоторого времени мы наблюдаем некоторый случайный процесс. При этом интересующая нас физическая величина регистрируется прибором в последовательные моменты времени. Каждое измерение физической величины будем называть событием. Множество таких событий за все время наблюдения несет полезную информацию о свойствах объекта. Задачей статистического анализа является извлечение этой информации. Различают два основных, базирующихся на статистическом и вероятностном подходах, метода анализа статистических закономерностей процессов.
Введем основные понятия и определения принятые в статистических методах обработки информации.
Вероятность события.
Если в результате N измерений некоторое значение случайной величины x повторилось в ni случаях, то вероятность реализации этой величины определяется как
(1)
Случайные дискретные величины. Случайная величина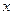 
называется дискретной, если она может принимать счетное множество значений. Она характеризуется значениями 
и вероятностями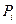 
с которыми реализуются эти значения. Очевидно, должно удовлетворяться равенство 
, которое называют условием нормировки. Множество значений 
образует дискретное распределение вероятности случайной величины x.
|
|
|
Рассмотрим некоторые примеры дискретных распределений.
а) Биномиальное распределение. В урне находятся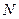 
шаров, из которых 
- белые. Из урны вынимается шарик и после регистрации снова возвращается в урну. Так повторяется 
раз. Какая вероятность того, что белый шарик будет зарегистрирована 
раз 
? Вероятность того, что в отдельном опыте будет извлеченный белый шарик 
, не белый - 
.
Искомая вероятность рассчитывается с помощью биномиального закона:
(2)
где 
- число сочетаний из элементов по .
Биномиальный закон описывает в самой общей форме вероятность события в выборке частиц с возвращением элементов.
б) Гипергеометрическое распределение. Рассматривается та же самая задача, которая и в а), но шарики не возвращаются в урну. Тогда вероятность того, что среди выбранных частиц будет белых, равняется
(3)
Гипергеометрическое распределение (3) описывает вероятность события в выборке без возвращения элементов.
в) Распределение Пуассона. Случайная дискретная величина называется распределенной по закону Пуассона, если она принимает счетное множество возможных значений 0, 1, 2,... с вероятностью
(4)
Число 
называется параметром распределения. Распределение Пуассона можно использовать в качестве красивого приближения биномиального распределения, если большое, а 
маленькое. Тогда за величину можно взять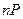 
.
Случайные непрерывные величины.
Пусть 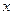– случайная величина, которая может принимать любые значения в интервале 
. Тогда число возможных значений 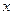обнаруживается бесконечным и неисчислимым. Поэтому 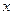называется непрерывной случайной величиной. Вероятность того, что величина 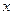находится в некотором малом интервале 
, определяется как
(5)
Здесь 
– называется плотностью распределения вероятности (или просто плотностью вероятности).
|
|
|
Очевидное следующее условие нормировки 
(6)
Одним из наиболее важных распределений, которые встречаются в физике (и вообще в статистике), есть нормальный или гауссовый закон распределения. Он имеет вид симметричной, колоколу подобной, кривой, которая определена в области (
, + 
). Функция плотности этого распределения описывается в виде:
(7)
Распределение (7) полностью определяется заданием двух параметров: 
и 
. Наоборот, во многих статистических задачах, в частности, в данной работе, допускают, что распределение является нормальным и тогда находят его параметры и .
На рис.1 изображенная функция для разных значений и .
Рис.1. Нормальный закон распределение.
1 - µ = 0, σ = 2; 2 - µ = 4, σ =1; 3 - µ = 2, σ = 4.
Нетрудно видеть, что наиболее ожидаемое значение случайная величина принимает при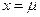 
. Это соответствует максимуму функции плотности вероятности.
При отклонении от 
значения функции быстро уменьшаются по экспоненциальному закону и стремятся к нулю на и + .
|
|
|
