 |
Моменты случайной величины.
|
|
|
|
В анализе результатов статических измерений важное значение имеют моменты случайной величины. Если известна плотность функции вероятности или функция вероятности, то можно использовать вероятностный подход к описанию статистических закономерностей изучаемого процесса. Тогда моменты определяются следующими правилами.
Моментом 
-го порядка случайной величины 
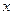называется
= 
(8)
где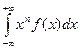 
- для непрерывного распределения случайной величины, 
- для дискретного распределения.
Центральным моментом –го порядка называется
= 
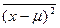(9)
где 
- для непрерывного распределения, а 
- для дискретного распределения.
Рассмотрим содержание этих величин на примере нормального распределения.
Первый момент представляет среднее арифметическое значение случайной величины 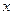или ее математическое ожидание:
Положим 
, тогда:
(10)
.
Второй центральный момент называется дисперсией (стандартным отклонением) и равняется
= 
= 
.
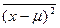Этот интеграл равен –
= 
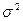(11)
Третий центральный момент называется эксцессом и характеризует асимметрию функции 
относительно значение 
. Для нормального распределения
= 
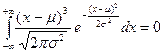, (12)
то есть в данном случае распределение плотности вероятности симметрично относительно 
.
Расчет показывает, что вероятность того, что результат измерения находится в границах одного стандартного отклонения 
(рис.2) равна 68%.
Рис.2.Функция плотности вероятности Гаусса
Заметим, что максимальное значение функции плотности вероятности есть:
(13)
Откуда можно найти по формуле
(14)
В экспериментах зачастую функция распределения случайной величины не известна, поэтому ограничиваются собственно статистическим методом анализа. В этом случае вводят статистические моменты, определяемые как средние значения соответствующих физических величин.
|
|
|
Так, например, средний квадрат случайной величины для N измерений находится из выражения:
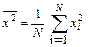
Гистограмма и распределение.
Серьезный статистический анализ результатов экспериментов требует многократных измерений. Первая задача состоит в том, чтобы найти методы записи большого количества вымеренных данных. Предположим, что мы провели измерения некоторой дискретной величины 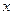, причем значение величины 
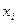встречается 
раз (табл. 10).
Таблица 1
| Значение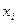
| ||||||
| Число реализаций,
| ||||||
Частота реализации, 
| 0,1 | 0,3 | 0,2 | 0,3 | 0,1 |
Графически эти значения можно задать гистограммой дискретной величины. Введем 
, где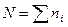 
- полное число измерений, - частота реализации результата .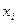
Среднее значение величины определяется как
(15)
Суть дискретной гистограммы передает рис. 3.
Рис. 3. Дискретная гистограмма для десяти значений случайной величины.
Однако в большинстве случаев измерение не приводит к целым значениям 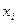. Например, вместо приведенных в таблицы значений можно получить: 23,9; 23,4; 24,2; 24,6; и т.д.
В этом случае удобно разбить весь диапазон возможных значений величины 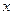на подходящее число интервалов (в нашем случае 5) и подсчитать, сколько значений попало в каждый интервал, например, от 23 до 24, от 24 до 25 и т.д. Если эти результаты нанести на график, получим гистограмму для непрерывной величины (рис. 4).
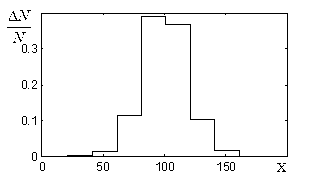
Рис. 4. Гистограмма для непрерывной величины.
В большинства случаев, при увеличении числа измерений гистограмма принимает некоторую определенную форму. Это видно из рисунка 5, где приведенные результаты 100 и 1000 измерений той же величины .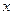
Рис. 5. Гистограммы распределения величин пр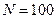и 
и 
.
Для 1000 измерений длину интервала уменьшили вдвое, и гистограмма становится регулярной и практически гладкой. С возрастанием числа измерений (предельно к бесконечности) распределение приближается к некоторой определенной предельной кривой, которое называют предельным распределением или генеральным распределением. Эту кривая изображена пунктирной линией. Следует подчеркнуть, что предельное распределение – это теоретическая идеализация, к которой никогда нельзя приблизиться абсолютно точно. Чем больше измерений, тем более близкой становится гистограмма к предельному распределению.
|
|
|
Очевидно, что в пределе
= 
. (16)
Поскольку ни в каком измерении нельзя точно определить истинное значение непрерывной величины, то не ясно, существует ли вообще истинное значение этой величины. Однако, удобнее считать, что любая физическая величина имеет истинное значение, которое задается генеральным распределением (вернее, значениями моментов, которые определяются из этого распределения). Поскольку в реальных измерениях мы имеем дело с конечным числом измерений, то возникает задача определения наилучшей оценки истинной величины и погрешности ее определения. В качестве таковых служат величины (16). Отметим, также, если у нас есть довольно надежные представления о виде предельного распределения , например, про его гауссовый вид, то значение и могут служить для определения его параметров 
и :
= 
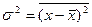(17)
|
|
|
