 |
Тестовое задание считается выполненным, если решена задача и даны 6 правильных ответов на тестовые вопросы.
|
|
|
|
Тестовое задание считается выполненным, если решена задача и даны 6 правильных ответов на тестовые вопросы.
2. Второй закон термодинамики. Энтропия, расчет энтропии системы в различных процессах.
Второй закон термодинамики устанавливает критерии необратимости термодинамических процессов и вводит новую термодинамическую функцию – энтропию.
Энтропия S – функция состояния, которая обладает следующим свойством: , где знак равенства относится к обратимым процессам, а знак больше - к необратимым.
Для изолированных систем dS ≥ 0, т. е. энтропия в изолированных систем в необратимых процессах может только возрастать, а в состоянии термодинамического равновесия она достигает максимума (dS = 0, d 2S < 0).
Энтропию можно определить с помощью двух эквивалентных подходов – статистического и термодинамического. Статистическое определение основано на идее о том, что необратимые процессы в термодинамике вызваны переходом в более вероятное состояние, поэтому энтропию можно связать с вероятностью: S=klnW, где k = 1, 38·10-23 Дж/К – постоянная Больцмана (k = R/NA), W - так называемая термодинамическая вероятность, т. е. число микросостояний, которые соответствуют данному макросостоянию системы.
Термодинамическое определение энтропии основано на рассмотрении обратимых процессов: 
.
Расчет изменения энтропии для различных процессов:
1) Нагревание или охлаждение при постоянном давлении. 
Если теплоемкость не зависит от температуры в интервале от T1 до T2, то 
.
2) Изотермическое расширение или сжатие. 
3) Фазовые переходы. При обратимом фазовом переходе температура остается постоянной, а теплота фазового перехода при постоянном давлении равна Δ Hф. п. , поэтому изменение энтропии равно: 
|
|
|
4) Смешение идеальных газов при постоянных температуре и давлении.
Если n1 моль одного газа, занимающего объем V1, смешиваются с n2 моль другого газа, занимающего объем V2, то общий объем будет равен V1 + V2, причем газы расширяются независимо друг от друга и общее изменение энтропии равно сумме изменений энтропии каждого газа:
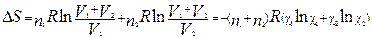, где xi - мольная доля i-го газа в полученной газовой смеси.
В отличие от многих других термодинамических функций, энтропия имеет точку отсчета, которая задается постулатом Планка (третьим законом термодинамики):
При абсолютном нуле T = 0 К все идеальные кристаллы имеют одинаковую энтропию, равную нулю.
Постулат Планка позволяет ввести понятие абсолютной энтропии вещества, т. е. энтропии, отсчитанной от нулевого значения при T = 0. Для расчета абсолютной энтропии веществ в стандартном состоянии надо знать зависимости теплоемкости Cp от температуры для каждой из фаз, а также температуры и энтальпии фазовых переходов. Так, например, абсолютная энтропия газообразного вещества в стандартном состоянии при температуре T складывается из следующих составляющих: 
В термодинамических таблицах обычно приводят значения абсолютной энтропии в стандартном состоянии при температуре 298 К.
Значения абсолютной энтропии веществ используют для расчета изменения энтропии в химических реакциях: 
.
3. Решение задач на тему «Второй закон термодинамики. Энтропия, расчет энтропии системы в различных процессах».
3-1. Определите изменение энтропии при плавлении 63, 5 г меди, если теплота плавления меди равна 12980 Дж/моль, а температура плавления меди 1083 °С.
3-2. Вычислите изменение энтропии при плавлении 100 г свинца, если температура плавления свинца 327, 4 °С, а теплота плавления 5485 Дж/моль.
3-3. В двух сосудах одинаковой емкости находится: в первом 2, 8 г азота, во втором 4 г аргона. Определите изменение энтропии при диффузии, возникающей в результате соединения сосудов с газами. Температура и давление постоянны.
|
|
|
3-4. Найдите изменение энтропии в процессе обратимого изотермического сжатия одного моль кислорода от 101, 3 до 1013 кПа.
3-5. Как изменится энтропия одного моль гелия при нагревании его от 20 до 70 °С, если объем газа при этом изменился от 24 до28, 1 л?
3-6. Сто грамм воды, взятой при 25°С, превращены в пар с температурой 150 °С и давлением 101, 3 кПа. Вычислите изменение энтропии этого перехода, если удельная теплота испарения воды при 100 °С равна 2257 Дж/г, удельная теплоемкость воды 4, 187 Дж/г·К, а удельная теплоемкость водяного пара при давлении 101, 3 кПа равна 1, 968 Дж/г·К.
3-7. Рассчитайте изменение энтропии при смешении 1 моль водорода с 1 моль азота при давлении 101, 3 кПа и постоянной температуре.
3-8. Найдите изменение энтропии при переходе трех моль кислорода от объема 33, 6 л под давлением в 202, 6 кПа к объему 67, 2 л под давлением 101, 3 кПа. Мольная теплоемкость кислорода Ср равна 29, 37 Дж/моль·К, температура постоянна.
3-9. Используя справочные данные, рассчитайте изменение энтропии при протекании реакции при стандартных условиях H2SO4 + 3H2S = 4S + 4H2O.
3-10. Используя справочные данные, рассчитайте изменение энтропии при протекании реакции при стандартных условиях 2HBr + H2SO4 = Br2 + SO2 + 2H2O.
3-11. Используя справочные данные рассчитайте изменение энтропии при протекании реакции при 500 °С C + 2H2SO4 = CO2 + 2SO2 + 2H2O.
3-12. Используя справочные данные рассчитайте изменение энтропии при протекании реакции при 300 °С SO2 + NO2 + H2O = H2SO4 + NO.
|
|
|
