 |
6. Задание для самостоятельной работы.
|
|
|
|
6. Задание для самостоятельной работы.
Рассчитайте изменение энергии Гиббса и значение константы равновесия выбранной вами реакции при данной температуре.
Занятие № 6.
План занятий:
1. Тестовый контроль знаний по теме «Термодинамические потенциалы. Химическое равновесие».
2. Лабораторная работа.
1. Тестовый контроль знаний по теме «Термодинамические потенциалы. Химическое равновесие».
1. Выберете уравнение (в дифференциальной форме) зависимости изобарно-изотермического потенциала от давления и температуры (при отсутствии всех видов работы, кроме работы расширения).
1. dG = –VdP – SdT. 2. dG = TdS – SdT. 3. dG = TdS + PdV. 4. dG = VdP – SdT.
2. За счет чего совершается максимальная полезная работа химической реакции при постоянных давлении и температуре?
1. За счёт убыли свободной энтальпии системы: 
.
2. За счёт убыли свободной энергии системы: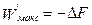 
.
3. За счёт убыли энтальпии системы: 
.
4. За счёт убыли внутренней энергии системы: 
.
3. Процесс протекает в условиях постоянства температуры и объема. Какой термодинамический потенциал следует выбрать в качестве критерия самопроизвольного протекания процесса в этих условиях?
1. Внутреннюю энергию U. 2. Свободную энтальпию G.
3. Свободную энергию F. 4. Энтальпию Н.
4. При каких условиях максимальная работа в системе совершается за счет убыли изобарно-изотермического потенциала (свободной энтальпии) Δ G?
1. В обратимом процессе при постоянных температуре и объеме.
2. В обратимом процессе при постоянных давлении и температуре.
3. В необратимом процессе при постоянных объеме и температуре.
|
|
|
4. В необратимом процессе при постоянных давлении и температуре.
5. Выберете формулу, устанавливающую связь между изменениями свободной энергии ∆ F к свободной энтальпии ∆ G при изотермическом расширении 1 моля идеального газа от объема V1 до объема V2.
1. Δ G= Δ F+ RT; 2. Δ F= Δ G+ RT; 3. Δ G= Δ F+ pΔ V; 4. Δ G= Δ F.
6. При каких условиях величина -∆ Н равна максимальной полезной работе?
1. Величина Δ Н никогда не равна работе.
2. В любом необратимом процессе.
3. В обратимом процессе при постоянных давлении и температуре.
4. В обратимом процессе при постоянных энтропии и температуре.
7. . Как изменяется энтропия (при постоянстве внутренней энергии и объема) и изобарно-изотермический потенциал (при постоянстве давления и температуры) при протекании самопроизвольного процесса?
1. Δ S > 0; Δ G < 0. 2. Δ S = 0; Δ G = 0. 3. Δ S > 0; Δ G > 0. 4. Δ S < 0; Δ G > 0.
8. В каких случаях термодинамические функции приобретают свойства термодинамических потенциалов?
1. При условии, если процесс протекает в изолированной системе при постоянной температуре.
2. В случае обратимого протекания процесса.
3. Такие термодинамические функции какH, U, F и G всегда являются термодинамическими потенциалами.
4. При таких условиях обратимого протекания процессов, при которых убыль соответствующей термодинамической функции равна максимальной полезной работе процесса.
9. Реакции, равновесие которых при увеличении давления смещается вправо (в сторону продуктов), –...
10. Реакции, равновесие которых при изобарном разбавлении инертным газом смещается вправо (в сторону продуктов):
Задача №1. Вычислить изменение энергии Гиббса при температуре 25 °С для реакции: 2СО2 = 2СО + О2.
Задача №2. Вычислить изменение энергии Гиббса при температуре 25 °С для реакции: СО + Н2О = СО2 + Н2.
Задача №3. Вычислить изменение энергии Гиббса при температуре 25 °С для реакции: 2HI = H2 + I2.
|
|
|
Задача №4. Вычислить изменение энергии Гиббса при температуре 25 °С для реакции: СО + 2Н2 = СН3ОН.
Задача №5. Вычислить изменение энергии Гиббса при температуре 25 °С для реакции: 3Н2 + N2 = 2NН3.
Задача №6. Константа равновесия реакции CO + H2O↔ CO2 + H2 при 800 К равна 4, 12. Смесь из 20 % СО и 80 % Н2О (по массе) нагревают до 800 К. Определить состав смеси при достижении равновесия и выход водорода, если был взят 1 кг водяного пара.
Задача №7. Константа равновесия реакции H2 + I2↔ 2HI при 717 К равна 46, 7. Определить количество разложившегося HI при нагревании 1 кмоль HI до 717 К.
Задача №8. Определить константы равновесия Кр и Кс реакции диссоциации I2 при нагревании 1, 518·10-3 моль йода до 1073 К, если его пары займут объем, равный 0, 2493 л при давлении 58, 1 кПа.
Задача №9. Вычислить давление и степень диссоциации N2O4, если при 323 К 1000 моль N2O4 находится в сосуде объемом 75·103 л. Определить исходное давление N2O4. Если 1000 моль N2O4 при температуре 323 К поместить в сосуд объемом 125·103 л, то при достижении равновесия в сосуде установится давление 34, 85 кПа.
Задача №10. При 500 К константа равновесия реакции РСl5↔ Сl2+РСl3 Kр = 3, 378·104. Определить степень диссоциации РСl5 при этой температуре, если при достижении равновесия устанавливается общее давление 81, 06 кПа. При каком общем давлении в системе степень диссоциации PCI5 будет равна 70%?
|
|
|
