Решение. 4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии. Составление отчёта

Решение.

1. Разобьем сечение на профили проката: два уголка 56× 4 и швеллер №18. Обозначим их 1, 2, 3 (см. рис. 11, а).

2.  Укажем центры тяжести каждого профиля, используя табл. 1 и 4 прил. I, и обозначим их С₁, С₂, С₃.

3.  Выберем систему координатных осей. Ось у совместим с осью симметрии, а ось х проведем через центры тяжести уголков.

Рис. 11

4. Определим координаты центра тяжести всего сечения. Так как ось у совпадает с осью симметрии, то она проходит через центр тяжести сечения, поэтому х_С = 0. Координату у_С опреде­лим по формуле

Пользуясь табл. 1 и 4 прил. I, определим площади каждого профиля и координаты центров тяжести:

А₁= 4, 38 см², у₁= 0; А₂= 4, 38 см², у₂= 0;

А₃= 20, 7 см², у₃= z_0(yг) + z_0(шв) = 1, 52 + 1, 94 = 3, 46 см.

Координаты у₁и у₂равны нулю, так как ось х проходит через центры тяжести уголков. Подставим полученные значения в формулу для определения у_С:

см.

5. Укажем центр тяжести сечения на рис. 8, а и обозначим его буквой С. Покажем расстояние у_С = 2, 43 см от оси х до точ­ки С.

Поскольку уголки симметрично расположены, имеют одина­ковую площадь и координаты, то А₁= А₂, у₁ = у₂. Поэтому фор­мула для определения у_С может быть упрощена:

.

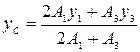6. Выполним проверку. Для этого ось х проведем по нижнему краю полки уголка (рис. 11, б). Ось у оставим, как в первом решении. Формулы для определения х_С и у_С не изменяются:

.

Площади профилей останутся такими же, а координаты центров тяжестей уголков и швеллера изменятся. Выпишем их:

А₁ = А₂ = 4, 38 см²; у₁+ у₂= b_уг – z_0(уг) = 5, 6 – 1, 52 = 4, 08 см;

А₃ = 20, 7 см²; у₃ = b_уг + z_0(шв) = 5, 6 + 1, 94 = 7, 54 см.

Находим координату центра тяжести:

см.

По найденным координатам х_С и у_С наносим на рисунок точ­ку С. Найденное двумя способами положение центра тяжести находится в одной и той же точке. Проверим это. Разница между координатами у_С, найденными при первом и втором решении, составляет: 6, 51 – 2, 43 = 4, 08 см.

Это равно расстоянию между осями х при первом и втором решении: 5, 6 – 1, 52 = 4, 08 см.

Ответ: у_С = 2, 43 см, если ось х проходит через центры тяже­сти уголков, или у_С = 6, 51 см, если ось х проходит по нижнему краю полки уголка.

Пример 8. Определить координаты центра тяжести сечения, изображенного на рис. 12, а. Сечение состоит из двутавра №24 и швеллера №24 а. Показать положение центра тяжести на сече­нии.

 

Рис. 12

Решение.

1. Разобьем сечение на профили проката: двутавр и швеллер. Обозначим их цифрами 1 и 2.

2.  Укажем центры тяжести каждого профиля С₁ и С₂, ис­пользуя табл. 3 и 4 прил. I.

3.  Выберем систему осей координат. Ось х совместим с осью симметрии, а ось у проведем через центр тяжести двутавра.

4. Определим координаты центра тяжести сечения. Координа­та у_С = 0, так как ось х совпадает с осью симметрии. Координату х_С определим по формуле

.

По табл. 3 и 4 прил. I и схеме сечения определим

А₁ = 34, 8 см²; х₁ = 0;

А₂ = 32, 9 см²; х₂ = b_дв/2 + b_шв – z_0(шв) = 11, 5/2 + 9, 5 – 2, 67 = 12, 58 см.

Подставим числовые значения в формулу и получим

см

5. Нанесем точку С (центр тяжести сечения) по найденным значениям х_С и у_С (см. рис. 12, а).

6. Проверку решения необходимо выполнить самостоятельно при положении осей, как показано на рис. 12, б. В результате ре­шения получим х_С = 11, 86 см. Разница между значениями х_С при первом и втором решении равна 11, 86 – 6, 11 = 5, 75 см, что равно расстоянию между осями у при тех же решениях b_дв/2 = 5, 75 см.

Ответ: х_C = 6, 11 см, если ось у проходит через центр тяжести двутавра; х_C = 11, 86 см, если ось у проходит через левые крайние точки двутавра.

Задание для практической работы 4. Определить положение центра тяжести сечения, состоя­щего из профилей проката, по данным одного из вариантов, показан­ных на рис. 13.

 

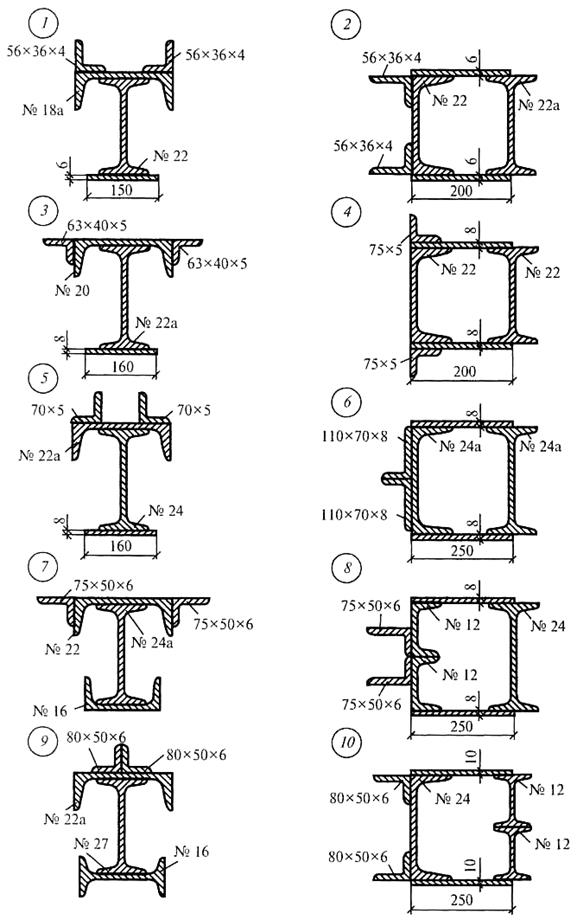
Рис. 13

Рис. 13. Продолжение

Рис. 13. Продолжение

Рис. 13. Окончание

Составление отчёта

Практическая работа выполняется в рабочей тетради для оформления практических работ по технической механике. Рисунок и расчётная схема выполняется карандашом. Записи ведутся чётко и грамотно чернилами чёрного или синего цвета. При выполнении практической работы рекомендуется использовать микрокалькулятор. Вариант задания выдаётся преподавателем по списку учебного журнала.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: