 |
Вопрос 6. Линеаризация уравнении динамики
|
|
|
|
Гидравлическая емкость представляет собой резервуар в котором имеется приток 
и сток 
. Основным параметром характеристики состояния уравнения 
.
Если степень открытия дросселя на стоке постоянно то уровень определяется разности между притоком и истинном. А если по условию работа 
может произвольно меняться то уровень принимается входной координатой.
Уравнение объекта переходном режиме запишется из уравнения материального баланса и уравнения истечения жидкости через гидравлическое сопротивление.
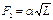, S – площадь поперечного сечения.
Электрическая емкость.
Дифференциальное уравнение электрической емкости запишется на основании закона Кирхгофа 
Объект с распределенными параметрами. Примером такого объекта может служить трубопровод.
Жидкость проходя внутри трубы изменяет свою температуру от начального до конечного 
при этом чтобы определить состояние объекта необходимо знать 
-ру жидкости в любой момент времени в любом сечении, следовательно уравнение динамики будет уравнением частных производных.
- коэффициент передачи
- линейная скорость жидкости.
Чтобы получить уравнение статики нужно прировнять к нулю производно по времени, в результате получим обыкновенное дифференциальное уравнение с производным по длине аппарата.
Вопрос 7. Переходные (динамические) характеристики объектов регулирования.снятиекривой разгона. Импульсная переходная функция.
Временные характеристики.
Динамические свойства объектов могут быть описаны дифференциальным уравнением, а могут быть представлены графическими характеристиками. Применяется 2 типа таких характеристик: Временные и частотные. С помощью этих характеристик можно определить реакцию объекта на произвольное внешнее воздействие.
|
|
|
Временные характеристики
1. Переходная характеристика 
представляет собой переходный процесс изменения во времени выходных величин звена вызванного ступенчатого воздействия 
.
Единичное воздействие 
это сигнал который мгновенно возрастает от 0 до 1 и дальше остается неизменной.
Уравнение описывающий переходный процесс в САУ при скачкообразном воздействии называется уравнением кривой разгона. А его график называется кривой разгона.
2. Импульсная переходная функция 
(весовой функцией) показывает реакцию объектов на единичный импульс обозначения: 
(дельта функции).
Единичный импульс – это импульс S которого равный 1 при высоте равной 
и основание равное 0.
Вопрос 8. Преобразование Лапласа
В теории автоматического управления широко используется специальный метод прикладного анализа, в основе которого лежит функциональное преобразование Лапласа.
Преобразование по Лапласу функции называется функцией комплексного переменного, которое определяется по формуле:
Здесь: 
- это исходная функция называемая оригиналом.
p – это оператор Лапласа 
, где 
- действительные переменные, 
-мнимые
Функция 
называется изображением по Лапласу функции 
- символ преобразования Лапласа
Обратный переход по Лапласу осуществим по формуле:
Для большинства функции существует таблица соответствует между изображением и оригиналом.
Широкое применение преобразования Лапласа объясняется рядом преимуществ над прямым решением в области действительного переменного.
Например: изображение многих функции гораздо проще оригинала.
Оригинал является разрывной функции времени
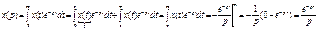
Изображение разрывной функции является непрерывной функцией от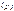 
|
|
|
