 |
Вопрос 17. Консервативное звено
|
|
|
|
Является частным случаем статического звена 2го опорядка у которого 
Консервативное звено отражает идеальный случай когда в рассеиванием энергии в звене можно пренебречь.
Переходной характеристикой такого звена имеет вид незатухающих колебаний.
Уравнение такого звена: 
АФХ: 
АЧХ: 
ФЧХ: 
Логарифмическая характеристика.
Вопрос 18. Идеальное интегрирующие звено.
Уравнение такого звена:
Выходной сигнал интегрирующего звена равного интегралу по времени выходного сигнала умноженное на постоянный коэффициент.
Пример интегрирующего звеньев является различные счетчики, суммирующие количества или энергии за определенный промежуток времени. Также примером может служить гидравлическая емкость, у которого в качестве выходного сигнала принимается уровень а в качестве входного разность между притоком и истоком.
Частотные характеристики:
АФХ: 
АЧХ: 
ФЧХ: 
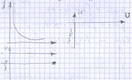
Таким образом АЧХ является функцией частоты, ФЧХ не зависит от частоты 
то есть гармонические колебания на выходе звена отстают по фазе от входных на 
. АФХ является мнимой функцией частоты и положительные частоты совпадают с мнимой полуосей.
Переходную характеристику получим из уравнения интегрирующего звена подстановкой вместо 
1 ступенчатого воздействие и единичного импульса 
Если на вход 
:
Таким образом при передачи на вход постоянного возмущения выходная величена, возрастает до бесконечности с постоянной скоростью. Реакция звена на единичный импульс является ступенчатая функция равной k
Логарифмическая характеристика: 
Вопрос 19. Идеальное дифференцирующее звено.
1. Идеальное дифференцирующие звено 
То есть координата пропорциональна скорости изменения входной. Параметр который называется постоянной дифференцирования (измеряется в секундах)
|
|
|
Отсюда найдем передаточную функцию и поле соответствующих преобразований частотной характеристики: 
АФХ: 
АЧХ: 
ФЧХ: 
Кривая разгона: 
То есть представляет собой импульс площадь которого равен k
Вопрос 20. Реальное диференциируещее звено.
Идеального дифференцирующего звена в природе не существует поэтому в качестве простейшего рассмотрим реальное дифференцирующие звено, которое описывается уравнением следующего вида.
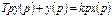
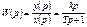
Как видно из полученной формулы реальное дифференцирующие звено на является элементарным а представляет собой цепочку, состоящую идеального дифференцирующего звена с передаточной функцией 
и апериодического звена 1 порядка с передаточной функцией 
Частотные характеристики:
АФХ 
АЧХ: 
ФЧХ: 
АЧХ реального дифференциального звена, так же как идеального возрастает с увеличением частоты, но ее верхний придел ограничен величиной 
. ФЧХ с увеличением частоты увеличивает от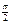 
до 0. Годограф лежит в 1ом квадрате и представляет собой полуокружность с центром в точке 
и диаметром 
Уравнение кривой разгона: 
Оригинал имеет вид: 
Импульсная переходная характеристика определяется от кривой разгона: 
Вопрос 21.Звено чистого запаздывания.
Это звено без искажения воспроизводит на выходе входную величину, как идеальное статическое звено, с той разницей, что выходная величина запаздывает по отношению к входной на постоянное время.
причем 
если 
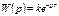
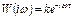
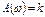
АЧХ не зависит от частоты 
ФЧХ с увеличением частоты уменьшается с 0 до 
, следовательно годограф АФХ представляет собой окружность с центром в начале координат с радиусом k.
|
|
|
