Вопрос 27. Понятие устойчивости.

Устойчивость – это свойство системы возвращается в исходный установившийся режим, после выхода из него в результате какого-либо внешнего воздействия.

Различают три типа систем.

1) устойчивый - эта система в которой будущей выведен из состояния равновесия, внешнего возмущения возвращается в исходное состояние равновесия.

2) нейтральные системы - это система которая после снятия возмущения приходя в состояния равновесия отличное от исходного.

3) неустойчивое состояние – это система в которых не восстанавливается равновесие после снятие возмущение.

Если система неустойчива достаточно любого толчка, чтобы в ней начался расходящийся процесс ухода от исходного состояния равновесия. Этот процесс может быть апериодическим – 1, или колебательным.

Апериодический расходящийся процесс может например возникнуть в САУ, если неправильно подключить полярность регулятора (то есть полярность воздействия на объект) в результате чего, регулятор будет осуществлять не отрицательную а положительную обратную связь и будет при этом не устранять отклонение а действовать в обратном направлении.

Колебательный расходящийся процесс может возникнуть, например если принять очень большой коэффициент передачи. В результате управляющие устройство будет излишне энергично воздействовать на объект, в результате чего при каждом очередном возврате выходных координат первичного значения.
Параметр будет пересекать ось все с большей, в результате процесс будет расходящийся.

2) В случае устойчивой системы, переходной процесс вызванный возмущением со временем затихает апериодический (1) или колебательный (2). И система вновь возвращается в состояние равновесия. Поведение систем после снятия возмущения описывается однородным дифференциальным уравнением для линейного объекта, дифференциальное уравнение имеет вид: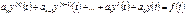

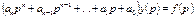
Для определения устойчивости системы достаточно решить характеристическое уравнение которое состоит в скобках 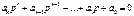решением этого уравнение является корни

При переходе в область действительного переменного получаем уравнение для . Корни характеристического уравнения являются комплексными переменами и могут изображены в комплексной плоскости при этом оси образуют пары сопряженных комплексных корней: .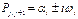

Действительная часть может быть как положительными так и отрицательными. При этом в зависимости от величины и знака действительной части корня возможно следующие варианты расположения корней в плоскости.

1. Все корни расположены в левой полуплоскости, то есть тогда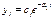

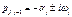
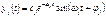
2. Все корни расположены в правой полуплоскости:

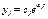
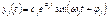
3. Корни расположены на мнимой оси: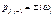

Каждая пара комплексно сопряженных корней дает составляющую переходного процесса, эта составляющая представляет собой синусоиду, с амплитудой изменяющеюся по экспоненте. И если то процесс будет затухающим, если то процесс будет расходящимся. Если 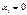будет не затухающиеся синусоидальные колебания.

Переходный процесс в САУ состоит из колебательных и апериодических составляющих. Колебательное соответствует паре комплексной сопряженной корней. Апериодическая действительному корню. Общим условием затухания всех составляющих и всего переходного процесса в САУ является отрицательность действительных частей всех корней.

Корень с положительной действительной частью, дает расходящиеся составляющую. Пара сопряженных мнимых корней дает не затухающиеся колебания.

Физические реальные САУ строится таким образом чтобы они всегда были устойчивы. Проктически все реальные системы не линейные их линеаризуют, ставится вопрос будет ли устойчивая реальная система, если устойчива линеаризованная.

Сформулируем 3 теоремы предложенным русским ученым Лякуновым.

Теорема 1

Если корни характеристического уравнения, линеаризованной системы содержит только отрицательные действительные части, то система будет устойчива и не какие добавки в виде различных нелинейности не сделают ее устойчивой.

Теорема 2

Если хотя бы один корень уравнения линеаризованной системы, имеет положительную действительную часть система будет неустойчива, и не какие добавки различных нелинейности не сделают ее устойчивой.

Теорема 3

Если корни уравнения линейной системы будут мнимыми, то система будет находится на границе устойчивости и вообще неизвестно как она себя поведет.