Вопрос 41. Определение настроек регулятора методом расширенных частотных характеристик.

При изучении условий устойчивости замкнутой системы по критерию Найквиста было отмечено что если разомкнутая система разомкнута и ее АФХ проходит через точку то замкнутая система будет находится на границе устойчивости.

Введение степени колебательности, равносильно введению новой границе устойчивости вместо мнимой оси АОВ:

 

Тогда по аналогии с критерием Найквиста можно сформулировать условие при котором замкнутая система будет обладать с замкнутой заданной системой.

Если разомкнутая система обладает степенью колебательности не ниже заданной ее РАФХ проходит через точку , то замкнутая система будет обладать ее заданной степенью колебательности.

(*)

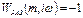
Полученное уравнение отражает связь между частотными характеристиками объекта и регулятора, вытекающего из условия обеспечения с заданной степенью колебательности.

Частотная характеристика объекта и выбранная степень калебательности m является заданным условием не известными остается настроечные параметры регулятора, и рабочая частота.

На 1^ом этапе определяется настройки регулятора сводятся к решению данной системы. Очевидно что для регулятора 2^мя и 3^мя настройками эта система имеет бесконечное множество решений. Поэтому только одной степени колебательности недостаточно, для нахождения настроек необходимо введение еще одного критерия, в качестве которого обычно используют интегральный квадратичный критерий, для которого оптимальное значение обеспечивает минимальное значение.

Расширенные настройки П - регулятора совпадают с обычными.

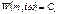
П: подставив в (*)

ПИ:

Подставим полученные уравнения в систему (*), получим выражение для настроек и

В этих уравнениях неизвестной величиной остается частота поэтому настройки соответственно степени колебательности может быть . Каждому значению частоты будет соответствовать своя пара настроек.

Если в плоскости настроечными параметрами построить кривые соответствуя различным степеням колебательности.

 

То эти кривые будут разбивать на 2 зоны, нижняя будет соответствовать большим значениям степени колебательности, а верхнее меньшим значением.

Кривая , разбивает на зону устойчивости и неустойчивости.

 

Сравнив между собой процессы регулирования соответствующим различным точкам на кривой раной колебательности М. В точке 1 отсутствует интегральная составляющая и в процессе регулирования появляется статическая ошибка. В точке 2 интегральная составляющая не значительна, статическая ошибка равна 0, но скорость устранения мала и переходный процесс характеризует затянувшимся хвостом. Увеличение интегральной составляющей сопровождается уменьшением рабочей частоты и ростом динамической ошибки точка 4. Расчет интегрального квадратичного критерия показал что его минимальное значение соответствует точке, не много сдвинутой в право относительно Max. Точка 3 рабочая частота в этой точке определяется

Таким образом методика нахождения настроек ПИ - регулятора сводится к следующему:

1) Расчет расширенных характеристик объекта.

2) Расчет и построение кривой равной колебательности, плоскости настроек и по формулам (1) и (2).

3) Нахождение по полученному графику рабочей частоты и соответствие ее оптимальных настроек.

ПИД – регулятор

Так же как Пи регулятор имеет две настройки и , методика расчета аналогична.

 

 

(*)

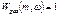
С помощью полученных формул из системы (*) выражаем настройки и :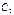

Подставим полученные формулы различных частот строим кривую равной колебательности:

 

На графике представлены различные переходные процессы с различными значениями настроек. В точке 1 кривой равной колебательности дифференциальной составляющей , регулятор ведет себя как довольно большой динамической и статической ошибкой. При движении в право по кривой наблюдается уменьшение статической и динамической ошибки. Дальнейшее увеличение настроек , приводит к уменьшению динамической ошибки но растет статическая. Поэтому оптимальными настройками являются соответствующие точке 2 чуть-чуть смещенные относительно max.

У ПИД регулятора 3 параметра настроек 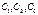и поэтому, его расчет по методу расширенных частотных характеристик несколько сложнее чем для регулятора с 2^мя параметрами.

Полученные формулы подставляем в рассмотрение ранее систему откуда выражаем и 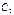: Для ПИД регулятора вместо плоскости параметров мы получим 3^х мерное пространство. В этом случае расчет настроек производится следующим образом, задаваясь различными значениями строят кривые равные колебательности в плоскости и :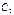

 

Эти графики должны быть аналогичны тем что получили для ПИ – регулятора, поскольку ПИ регулятор это частный случай ПИД регулятора у которого третья настройка ровна нулю. Затем для каждого графика находим оптимальные настройки и , сравнивая между собой переходные процессы соответственно теми или иными настройками. Выбирают оптимальный для которого интегральный квадратичный критерий будет оптимальным.

⇐ Предыдущая1234567Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: