 |
Идеальное статическое звено: (Усилительное или пропорциональное)
|
|
|
|
Эго уравнение и в статике и в динамике имеет вид: 
Таким образом сигнал усилительного звена в любой момент времени равен входному сигналу умноженного на постоянный коэффициент, его передаточная функция определяется из уравнения после преобразования по Лапласу: 

 . Заменив передаточную функцию оператор Лапласа на
. Заменив передаточную функцию оператор Лапласа на  получим частотную характеристику.
получим частотную характеристику.
АФХ: 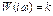 ; АЧХ:
; АЧХ:  ; ФЧХ:
; ФЧХ:  ;
;
Таким образом характеристики усилительного звена не зависит от частоты при чем ФЧХ = 0  усилительное звено не изменяя фазу гармонического сигнала а изменяя его амплитуду в k раз.
усилительное звено не изменяя фазу гармонического сигнала а изменяя его амплитуду в k раз.
3. Кривая разгона
Это звено идеализация реальных звеньев так как в действительности не одно звено не в состоянии равномерно пропускать все частоты от 0 до  , а имеет определенную полосу частот:
, а имеет определенную полосу частот:  . Например: реальные электронные усилители обладают некоторой инерционнальностью и их характеристики в действительности имеют вид
. Например: реальные электронные усилители обладают некоторой инерционнальностью и их характеристики в действительности имеют вид
Примеры усилительных звеньев:
Механический редуктор без инерционный усилитель делитель напряжения, рычажное соединение, первичное преобразование, датчики и так далее.
Логарифмическая характеристика:
Для идеального звена:


Вопрос 14. Статическое звено 1го порядков или апериодическая.
Линейное дифференциальное уравнение такого звена имеет вид:
 , где Т – const времени, k – коэффициент усиления.
, где Т – const времени, k – коэффициент усиления.
Примером такого звена может служить любая цепочка, включающая в себя сопротивление, и емкость независимо от их физической природы.
 Постоянная времени T зависит от сопротивления и емкости звена и характеризует инерционность звена (чем больше T тем больше инертность)
Постоянная времени T зависит от сопротивления и емкости звена и характеризует инерционность звена (чем больше T тем больше инертность)


Частотные характеристики
АФХ: 
АЧХ: 
ФЧХ: 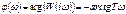

АЧХ апериодического звена на нулевой частоте равна коэффициенту усиления k с увеличением частоты, монотонно убывает 
|
|
|
ФЧХ с увеличением  частоты 0 до
частоты 0 до  изменяется 0 до
изменяется 0 до 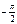 . Следовательно годограф целиком лежит в IV квадрате и представляет собой полуокружность в центре
. Следовательно годограф целиком лежит в IV квадрате и представляет собой полуокружность в центре  , с диаметром
, с диаметром  .
.
Временные характеристики:
Уравнение кривой рядом получим из передаточной функции следующим образом
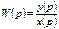



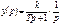 - уравнение разгона оператора Лапласа.
- уравнение разгона оператора Лапласа.

Аналогично находим импульсную переходную характеристику: 

Если эти характеристики найдены экспериментально, то по ним можно определить k и T и таким образом получить уравнение звена.
Величина T const определяется инерциональность звена, чем она больше тем больше длительность переходного процесса, на практике за длительность переходного процесса принимают время которое прошло от начала процесса до момента когда выходная координата достигается 95% своего конечного значения. В данном случае это время ЗТ
Логарифмическая характеристика

При малом значении частоты  :
: 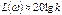
Соответственно характеристика будет представлять собой прямую параллельную оси абсциссе и отстающая от него 

Это 1ая асимптота которая стремится к графику ЛАЧХ при  . С другой стороны при больших частотах
. С другой стороны при больших частотах 
 в этом случае характеристика представляет собой прямую. “\”
в этом случае характеристика представляет собой прямую. “\”
Эта линия является 2ой асимптотой которая стремится к графику ЛАЧХ при  . Обе асимптоты пересекаются на частоте:
. Обе асимптоты пересекаются на частоте: 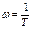 ,
, 
Частота  называется сопрягающей касательной.
называется сопрягающей касательной.
Таким образом расхождение между истиной и ассимтотичной ЛАЧХ составляет 3Дб, поэтому на практике при построения ЛАЧХ периодических звеньев используют ассимтоты.
Примеры апериодических звеньев 1го порядка: генератор const I, двигатель любого типа, резервуар с газом или жидкостью, нагревательная печь, термопара, гидропневмоусилители и так далее.
Вопрос 15. Статическое колебательное звено 2го порядка.
 здесь
здесь 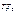 -const времени, k – коэффициент усиления.
-const времени, k – коэффициент усиления.
|
|
|
В соответствии с этим уравнением звено будет колебательным в том случаи, если соотношение  , если это неравенство не выполняется звено будет апериодическим 2го порядка.
, если это неравенство не выполняется звено будет апериодическим 2го порядка.
Уравнение статики имеет тот же вид что и для всех: 

Частотные характеристики АФХ: 
АЧХ: 
ФЧХ: 

Как видно для формул АЧХ при малых значениях  :
: 
Наблюдается некоторое увеличение АЧХ.
Мах появляется на частоте  , в предельном случае
, в предельном случае  , на этой частоте появляется резонансный пик.
, на этой частоте появляется резонансный пик.
Временные характеристики.

По экспериментально снятым кривым так же можно определить значение 
Логарифмическая характеристика.
Асимптотическая ЛАХ представляет собой ломанную линию, состоящую из 2х асимптот одна из которых параллельна оси абсциссе и отстает от нее на расстояние  , 2ая имеет наклон -40 дц/дек. Точка пересечения соответствует частоте
, 2ая имеет наклон -40 дц/дек. Точка пересечения соответствует частоте 

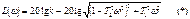
Уравнение для 1ой асимптоты получим из (*) при условии  . В этом случае
. В этом случае 
Уравнение 2ой асимптоты также получается из (*), при условии 


Введем коэффициенты 
Если  , то реальная логарифмическая характеристика можно заменить ассимтотической.
, то реальная логарифмическая характеристика можно заменить ассимтотической.
Колебательные звенья это система способна накапливать 2 вида энергии кинетическую и потенциальную энергию. Процесс колебания сопровождается переходом от одного вида к другому. При этом время  характеризует способность системы демпфировать (тормозить) колебания, а время
характеризует способность системы демпфировать (тормозить) колебания, а время  способность раскачивать.
способность раскачивать.
Примеры колебательных звеньев:
Электрический резонанс контур включает в себя R L C; Электродвигатель при достаточно большой постоянной времени якорь, упруго механической передачи.
Вопрос 16. Статическое звено 2го порядка (Апериодическая 2го порядка)
Такое звено описывается уравнением, аналогичным колебательным при условии  . Обобщенный вид уравнения 2го порядка следующее:
. Обобщенный вид уравнения 2го порядка следующее:  .
.
 Апериодическое звено 2го порядка можно представить как цепочку из 2х первых звеньев I порядка, с постоянными
Апериодическое звено 2го порядка можно представить как цепочку из 2х первых звеньев I порядка, с постоянными  и
и  и коэффициентом усиления k и 1.
и коэффициентом усиления k и 1.
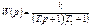
Отсюда
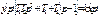 в операторной форме
в операторной форме
 - дифференциальное уравнение.
- дифференциальное уравнение.
Частотные характеристики.
АФХ: 

АЧХ: 
ФЧХ: 
Как следует из ФЧХ которая для положительных частот изменяется в пределах 0 до  . Годограф АФХ должен лежать в III и IV квадрате. Причем модуль с увеличением частоты от 0 до
. Годограф АФХ должен лежать в III и IV квадрате. Причем модуль с увеличением частоты от 0 до  , монотонно убывает от k до 0. на рис. пунктиром показано частотные характеристики 1го порядка с коэффициентом усиления k и постоянным значением
, монотонно убывает от k до 0. на рис. пунктиром показано частотные характеристики 1го порядка с коэффициентом усиления k и постоянным значением  . Как видно из рисунков добавление еще одного звена уменьшает значение модуля и увеличивает значение фазы.
. Как видно из рисунков добавление еще одного звена уменьшает значение модуля и увеличивает значение фазы.
|
|
|
Уравнение кривой разгона (переходной характеристики) в операторной форме имеет вид.

 Оригиналом данного уравнения будет следующие выражение:
Оригиналом данного уравнения будет следующие выражение:  где
где  ;
; 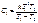 ;
;  ; график
; график  представляет собой неколебательную кривую точкой перегиба стремящиеся к k.
представляет собой неколебательную кривую точкой перегиба стремящиеся к k.
Уравнение импульса переходной характеристики  получим дифференцируя переходную характеристику:
получим дифференцируя переходную характеристику:


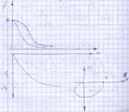
Логарифмическая характеристика предполагает собой ломаную из 3 асимптот.



|
|
|


