Микромоделирование ТП: принципы, законы алгоритмы.

Микромоделирование – такой метод, который представляет каждый авто индивидуально и для каждого авто создается свое дифференциальное уравнение в каждый момент времени индивидуально.

Преимущества микромоделей: возможность представления дорожных сетей в перегруженных состояниях, т.к. только микромодели позволяет имитировать очереди авто. Модели, применяемые при микромоделировании, позволяют получать результаты даже в условиях транспортного затора. Такая способность моделирования делает данный вид модели наиболее полезным для анализа движения в центрах городов. Существует несколько видов моделей, относящихся к микроскопическому моделированию.

В настоящее время основной вид представляет 2 модели: «модели, следящие за лидером» и «модели, основанные на клеточных автоматах».

В моделях следования за лидером, которые так ж называются непрерывными во времени моделями. В этих моделях все авто описываются обыкновенными дифференциальными уравнениями, которые учитывают параметры: местоположение авто Xa и Vавто. Предполагается, что действия каждого водителя ограничены его скоростью и расстоянием от его авто до бампера, впереди двигающегося авто:Sa=Xa-1-Xa-la-1, a – второй авто; a-1 – лидер. Это уравнение можно преобразовать в формулу ускорения второго авто, которое будет зависеть от действия водителя: Xa(t)=Va(t)=F(Va(t),Sa(t),Va-1(t)); Va(t)=F(Xa(t),Va(t),Xa-1(t),…,Xa-na(t),Va-na(t)). Исходя из уравнения можно говорить, что поведение водителя ведомого авто зависит не только от разности скоростей авто-лидера и второго авто, но и от других ТС, находящихся в ТП.

На этих идеях основаны следующие варианты моделей следования за «лидером»:

1) Модель оптимальной скорости. (Watanabe). В ней предполагается, что водитель 2авто всегда будет сохранять максимальную с его точки зрения V до тех пор, пока остается запас расстояния до лидера. При этом, водитель старается выбрать свою V оптимальной, исходя из расстояния до лидера в том случае, если зазор безопасности снижается.

2) Модель Видемана – немецкий ученый. Согласно ей предполагается, что водитель ведомого авто может находиться в одном из четырех состояний: -условие свободного движения, водитель старается развить и поддерживать свою желаемую V. Это возможно только в этих условиях, в реальных ДУ, текущая V редко совпадает с желаемой; -приближение, водитель ведомого авто как бы приближается к лидеру в процессе снижения V самого процесса. Приближаясь к лидеру, водитель 2авто тормозит настолько, чтобы разница в скоростях 2х авто стала =0 в тот момент, когда ведомый приблизится к лидеру на минимально безопасное расстояние; -следование, водитель 2авто следует за лидером без ускорения и замедления, поддерживая дистанцию м/у ними = постоянной; -торможение, применение рабочего/аварийного торможения, если дистанция м/у авто становится меньше безопасной, это вызывается: резким торможением лидером (по причине такого маневра, как подстава). Вывод: по этой модели для каждого режима ускорения рассчитывается как результат влияния таких факторов: -текущая V двух авто; -разница в скоростях двух авто; -индивидуальные особенности водителя; -особенности самого второго авто. Видеман предлагает установить, когда водитель переходит из одного состояния в другое по достижению определенного барьера, он определяется разницей в скоростях движения ведомого и лидера. Т.к. эту разницу оценивает водитель второго авто, то эта модель получила второе название – психофизиологическая модель следования.

3) Модель умного водителя. Для авто «а» описывает его положение в момент времени t, скоростью V, его местоположением Xa. В упрощенном виде: Sa= Xa-1-Xa-la-1. Разница м/у скоростями6 ∆Va=Va-Va-1. Движение авто ведомого описывается двумя уравнениями: x_а=dx_a/dt=V_a и 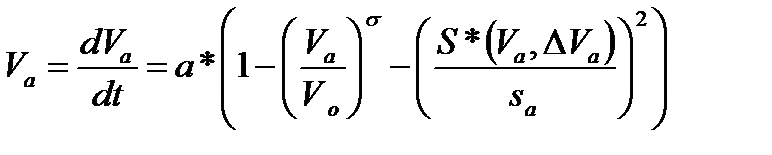, В этой модели предполагается, что d/b 2авто может зависеть от двух условий движения: ускорение/замедление на свободной дороге и при взаимодействии авто в ТП.

1)Поведение в условиях свободного движения будет описано алгоритмом: расстояние до авто-лидера является достаточно большим и следовательно ускорение ведомого авто находится в большей зависимости от V свободного движения, которая ~ стремлению V_a к V_o, следовательно ведомый авто на свободной дороге величину своей скорости будет асимптотически приблежать к V свободного движения. 2)Поведение на загруженной дороге: при большой разности скоростей ведомого авто и авто лидера и при разности в расстояниях, ускорение/замедление будет определяться: -a*(V_a*ΔV_a)²/(2*S_a*_[d*b)=-(V_a*ΔV_a)²|(4*b*S_a²). Это замедление приводит к компенсации разности скоростей за счет торможения на превосходящего величину b. 3)поведение на малых дистанциях между ведомым и авто-лидером характеризуется: небольшой разностью в скоростях и следовательно: -a*(S_o+V_a*T)²/S_a² – она показывает, что ведомый авто отстает достаточно от лидера, чтобы обеспечить безопасную дистанцию.

Динамическая теория движения плотных потоков авто. Взаимодействие между авто в плотном потоке само по себе зависит от поведения водителей этих авто, и проявляется в постоянном изменении дистанции между авто. Поэтому впервые динамические теории были разработаны с целью расчета дистанции между авто при разных V движении. Первым допущением таких авто было: движение осуществляется в колонне без обгонов и без наездов. Сейчас выделяют 4 варианта упрощенных моделей. Все они основаны на разных начальных условиях. 1группа: в них не учитывается тормозной путь. d=l_а+l_р+l_о, d – мин безопасное расстояние между авто, l_а – длина авто-лидера, l_р – путь, проходимый ведомым авто за время реакции водителя, l_о – зазор безопасности. Анализ уравнений показывает большое различие дистанции между авто, которое вызывается различием во времени реакции разных водителей. «-»: отсутствие учета тормозных качеств. 2группа: учитывается полный тормозной путь 2го авто при остановке первого. d=l_p+l_t+l_a+l_o; l_t=V²|(2*g*φ) – тормозной путь. По сравнению с уравнением первой группы эта более реально отражает условия движения, но все таки очевидна разница по графику в расчетах, вызванная тем, что берется во внимание тормозного пути только одного авто. 3группа: учитывается разница в тормозных путях авто лидера и ведомого. Уравнения основаны на очевидных предпосылках, что ведомый и ведущий авто тормозят с разной интенсивностью/замедлением. d=l_p+l_t2-l_t1+l_a+l_o. Уравнение является общим случаем 1 и 2 групп. Например, если разница l_t2-l_t1=0, то уравнение 3группы превращается в уравнение 1группы, если l_t1=0, то в уравнение 2группы. Все это означает, что уравнение 3группы более универсальные и более применимые, чем 1 и 2 группы.

Динамическая теория следования за лидером. Допущением в этой теории служит гипотеза о том, что авто двигаются в колонне друг за другом не совершая обгоны, и со V разрешенной ПДД. Дифференциальное уравнение теории получается из схемы 1. Уравнение: x_n+1=x_n+(l₀+t_p*V_n+1)+l_n. (1). l₀ – мин расстояние между ведомым и ведущим авто при остановке; t_p*V_n+1 – расстояние между авто, которое устанавливается в зависимости от V движения; l_n – длина ведущего; x – координаты. Дифференцируя уравнение 1 по времени, получаем: (2) Второе уравнение может быть выражено через V: (3) В 3 уравнении dV_n+1/dt – ускорение ведомого авто; V_n+1-V_n – разница скоростей автомобилей. Это уравнение первое дифференциальное теории следования за лидером. Оно формулируется6 при следовании друг за другом двух авто на достаточно близком расстоянии, когда проявляется их взаимное влияние, ускорение ведомого авто прямопропорционально разнице в скоростях ведомого и ведущего.

Первый закон. 1/t_p – α1 – коэф. Пропорциональности/чувствительность водителя. Уравнение 3 можно переписать: dV_n+1/dt=α1(V_n+1-V_n). Первый закон можно трактовать: водитель ведомого авто реагирует на какое то внешнее раздражение в соответствии с соотношением: (реакция)t+t_p=α1(воздействие). Реакцией является ускорение/замедление ведомого авто, а воздействие – разность скоростей двух авто. Ряд ученых предположили, что чувствительность водителя обратно пропорционально дистанции между авто ведомого и ведущего. α1=V_o/d. Такой подход позволил создать 2 уравнение теории: 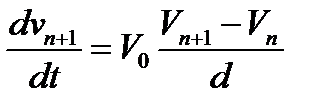. Второй закон: ускорение ведомого авто прямо пропорционально разнице скоростей и обратно пропорционально дистанции между авто. Была получена зависимость, означающая, что чувствительность водителя изменяется с изменением V в соотношении: чем ↑Vдвижения, тем ↑ чувствительность.

Модели, основанные на клеточных автоматах. В них применяется концепция, предложенная Фон Нейманом, немецкий ученый. Формулировка исходной модели Нагеля и Шрекенберга состоит в: Пусть x_n и V_n – координаты V ведомого. Допустим, что дистанция до авто-лидера: d_n=x_n+1-x_n. V может принимать какое-то значение. При каждом шаге времени t→t+1 состояние всех авто на дороге будет обновляться, исходя из правил: 1)Ускорение. Если V_n<V_max, то V ведомого будет ↑ на единицу до тех пор, пока не достигнет максимальное значение: V_n=V_max. Если V достигала макс, то дальше не меняется, и: V_n→min. 2) Торможение. Если дистанция меньше V: d≤V_n, то V ведомого должна ↓ до d_n-1. 3)Случайные возмущения в ТП, если V ведомого > 0, то V этого авто м.б. уменьшена ровно на 1 с определенной вероятностью до тех пор, пока она не станет =0. 4)Собственно движение. Каждое авто продвигается вперед на такое количество ячеек, которое соответствует новой V авто после выполнения шагов 1,2,3. 1й шаг отражает общее стремление всех водителей ехать как можно быстрее4 2й – гарантирует отсутствие столкновений с впереди едущим авто; 3й – отражает элемент случайности, который учитывает поведение всех водителей в ТП.

Теория клеточных автоматов строится на принципе, что и приращение перемещения Δx и приращение времени Δt, и приращение ΔV принимается за единицу, следовательно, каждый отрезок дороги м.б. занята авто, или быть пустой. Как правило, за единицу времени принимается среднее время реакции водителя. Если мы считаем Δt=const, тогда размер ячейки будет определять дискретность нашей модели. В условиях полного затора, расстояние, занимаемое одним авто, составляет 6м. Ученые пришли к выводу, что клеточная модель не отвечает реальным условиям и величину одной клетки нужно выбирать по другому. Они используются при моделировании из за того, что могут воспроизводить неограниченное количество ситуаций на дороге по простым алгоритмам, но они не обладают высокой точностью.