 |
Вероятность. Понятие о дискретных и непрерывных случайных величинах. Законы распределения случайной величины.
|
|
|
|
Вероятность события pi – число, заключенное между 0 и 1, характеризующее среднюю частоту появления в измерениях того или иного значения СВ.
ДСВ можно полностью задать вероятностным рядом, указав вероятность pi для каждого значения xi.
Дискретными СВ (ДСВ) наз. случайные величины, возможные значения которых есть отдельные изолированные числа (т.е. между двумя соседними значениями нет возможных значений), например, количество единиц оборудования в цехе, количество циклов прессования керамической плитки в сутки. ПустьДСВX может принимать в результате опыта значения x1, x2,…,xk. Отношение числа опытов mi, в результате которых СВ X приняла значение xi, к общему числу произведенных опытов n называется частотой появления события. Частота mi/n сама является СВ и меняется в зависимости от количества произведенных опытов. Но при большом числе опытов она имеет тенденцию стабилизироваться около некоторого значения pi, называемого вероятностью события: 
Непрерывными СВ (НСВ) называются СВ, принимающие любые значения на некотором промежутке числовой оси (время, температура обжига, давление прессования керамической плитки, расход топлива на варку стекла, физико-химические свойства получаемого материала).
Вероятность того, что НСВ точно примет заданное значение, равна нулю. Число значений так велико, что для большинства из них вероятность принять эти значения равна нулю, т.е. событие может произойти, а вероятность его равна нулю. Для НСВопределяется вероятность того, что в результате опыта ее значение попадет в некоторый интервал.
Удобно пользоваться вероятностью событий X<x, где x – произвольное действительное число, а X – СВ. Эта вероятность является функцией от x: 
|
|
|
и называется функцией распределения СВ (интегральная функция распределения).
В виде функции распределения можно задать распределение как НСВ, так и ДСВ (см. рисунок).
Рисунок – Функция распределения: а) НСВ; б) ДСВ
Значения функции распределения при предельных значениях аргумента соответственно равны 0 и 1.
Функция распределения ДСВ всегда есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям СВ, и равны вероятностям этих значений. Сумма всех скачков равна 1. Соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями, называется законом распределения.
Дифференциальная и интегральная функции распределения (плотность вероятности) случайной величины. Понятие математического ожидания и дисперсии случайной величины. Нормальный закон распределения случайной величины.
Интегральная функция распределения. Здесь вероятностью событий является X<x, где x – произвольное действительное число, а X – случайная величина. Эта вероятность является функцией от x:
и называется функцией распределения случайной величины.
Дифференциальная функция. Для непрерывной случайной величины(СВ) наиболее часто употребляется производная функции распределения – плотность распределения СВ f(x).
Площадь, ограниченная осью x, прямыми x=x1 и x=x2 и кривой плотности распределения, равна вероятности того, что СВ примет значения из интервала x1–x2:
В прикладных задачах вместо полного определения СВ в виде законов распределения вероятностей определяют числовые характеристики – числа, выражающие характерные особенности СВ, называемые моментами случайной величины.
Начальный момент первого порядка (k =1) называется математическим ожиданием (средним значением) СВ. Для НСВ математическое ожидание выражается интегралом:
|
|
|
Чаще, чем начальные моменты, применяются центральные моменты. Центральный момент k -того порядка для НСВ.
Второй центральный момент называется дисперсией.
Дисперсией СВ называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т. е.: 
Для Непрерывной СВ: 
Корень квадратный из второго центрального момента называется среднеквадратичным отклонением:
Практически все СВ в производстве строительных материалов подчиняются нормальному закону распределения с параметрами 
– среднее значениеи S – среднеквадратическое отклонение (закон распределения Гаусса).
Плотность распределения имеет вид:
Нормальный закон распределения широко используется при обработке результатов наблюдений, также его можно использовать для нахождения доли несоответствующих показателей или доли брака В. Если на показатель качества накладывается ограничение xст, регламентированное стандартом, то относительную долю дефектной продукции (брака) можно рассчитать по показателю качества:
С использованием значения Pk по специальным таблицам находят значение доли брака.
25. Построение матрицы планирования при полнофакторном эксперименте. Нулевой уровень. Интервал варьирования. Принципы оптимальности матрицы планирования.
Принципы построения матрицы планирования:
1) в первом столбце записывают значение фиктивной переменной x0=+1, во втором – знаки (+1 и –1) меняются поочередно, в третьем – через два, в четвертом – через четыре и т.д. по степеням двойки;
2) при добавлении нового фактора каждая комбинация нового плана встречается дважды: в сочетании с нижним и верхним уровнями нового фактора;
3) для фактора, отражающего взаимодействие (x1·x2, x1·x2·x3)новый столбец получают путем перемножения двух (трех и т.д.) столбцов исходного плана.
Например, матрица планирования для ПФЭ 23 в кодированных переменных будет выглядеть следующим образом.
| x0 | x1 | x2 | x3 | x1·x2 | x1·x3 | x2·x3 | x1·x2·x3 | yu |
| + + + + + + + + | – + – + – + – + | – – + + – – + + | – – – – + + + + | + – – + + – – + | + – + – – + – + | + + – – – – + + | – + + – + – – + | y1 y2 y3 y4 y5 y6 y7 y8 |
Нулевой уровень, или нулевая точка, фактора – это некоторое начальное значение фактора при составлении математической модели процесса. При выборе нулевых точек факторов следует руководствоваться условием «попадания» центра эксперимента в область оптимальных значений выходного параметра.
|
|
|
Интервал варьирования часть области определения фактора, выбранная симметрично относительно его нулевого уровня. Основное требование к интервалу варьирования состоит в том, чтобы он не превышал удвоенной среднеквадратичной ошибки фактора.
Матрица планирования ПФЭ обладает свойствами ортогональности и ротатабельности.
Ротатабельность предполагает минимум дисперсии предсказанного значения выходного параметра в любой точке факторного пространства при равенстве дисперсий в точках, расположенных на одинаковом расстоянии от центра плана.
Ортогональность позволяет при расчете коэффициентов уравнения регрессии по методу наименьших квадратов использовать следующие свойства:
;
;
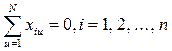В уравнениях п – число факторов, N – число опытов, и – номер опыта (и= 1, 2,..., N). Кроме того, ортогональность двух столбцов означает полное отсутствие корреляции соответствующих факторов.Следовательно, и оценки параметров оказываются некоррелированными. Это дает возможность оценить независимо влияние каждого фактора, а также легко упрощать модель, если какой-либо член окажется незначимым: такой член исключают из уравнения, и это никак не сказывается на величине остальных параметров. Некоррелированность позволяет к тому же легко проверить гипотезу о значимости факторов, что, как отмечалось выше, крайне сложно, если факторы не независимы.
После построения матрицы планирования приступают к проведению экспериментов. Важно отметить, что порядок опытов в матрице планирования не должен определять реальную последовательность выполнения опытов, т.е. они должны быть рандомизованы. Часто каждый опыт (каждая строка матрицы планирования) повторяется несколько раз – это делается для оценки дисперсии воспроизводимости. Другой прием, применяемый для оценки дисперсии воспроизводимости, – постановка специальной серии параллельных опытов в центре плана, т. е. в точке с координатами (0, 0, 0,.., 0).
|
|
|
Расчет коэффициентов регрессии проводят по формулам:
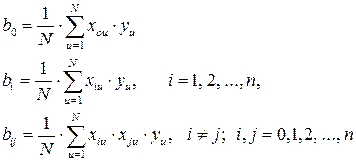
где bij – коэффициент регрессии, характеризующий взаимодействие факторов x iu·xju.
После вычисления коэффициентов регрессии переходят к статистическому анализу уравнения регрессии, который состоит из трех основных этапов: 1) оценка дисперсии воспроизводимости (или оценка ошибки опыта), 2) оценка значимости коэффициентов уравнения регрессии и 3) оценка адекватности модели.
|
|
|
