Генеральная совокупность, выборка. Статист. оценки. Проверка статист. гипотез.

Множество значений случайной величины, полученных в результате эксперимента или наблюдений над объектом исследования, представляет собой статистическую совокупность. Данная совокупность, содержащая в себе все возможные значения случайной величины, называется генеральной статистической совокупностью. Выборочной статистической совокупностью называется совокупность, в которой содержится только некоторая часть элементов генеральной. По результатам экспериментов практически всегда встречаются с выборочной, а не с генеральной совокупностью. Выборочную статистическую совокупность будем в дальнейшем называть выборкой, а число опытов (наблюдений) п, содержащееся в выборке, – объемом выборки.

При повторении опытов в одинаковых условиях обычно обнаруживается закономерность в частоте появления тех или иных результатов.

Перенос знаний от выборочной совокупности к генеральной может быть осуществлен лишь с некоторой вероятностью P{Θ}, т.е. суждение о генеральной совокупности носит вероятностный характер и содержит элемент риска (1-P{Θ}). Суждения о свойствах генеральной совокупности называются статистическими гипотезами. Их проверка осуществляется с помощью статистических критериев, назначаемых в зависимости от формулировки гипотезы H.

Основная выдвинутая гипотеза называется нуль-гипотеза (H₀). Противоречащие ей гипотезы H_i называют альтернативными, или конкурирующими.

Нуль-гипотеза Н₀: между обеими выборками нет существенной разницы, обе они принадлежат одной генеральной совокупности, а имеющиеся различия обусловлены случайным характером выборок, например, влиянием случайных ошибок. В этом случае любые оценки, рассчитанные по этим двум выборкам, будут оценками одних и тех же генеральных (истинных) значений; тогда в большинстве случаев имеет смысл объединить обе выборки в одну, увеличив тем самым число степеней свободы.

Противоположная, или альтернативная гипотеза H₁ различия объясняются не случайностью, а существом дела. Выборки относятся к разным генеральным совокупностям. Поскольку проверка гипотез ведется по выборке, то могут возникнуть ошибки двух родов. Если будет отвергнута правильная гипотеза, то совершается ошибка первого рода, если будет допущена неправильная гипотеза, то совершается ошибка второго рода.

Вероятность допустить ошибку первого рода называется уровнем значимости и обозначается α. Область, отвечающая вероятности α, называется критической, а дополняющая ее область, вероятность попадания в некоторую P{Θ_α}=1-α, называется областью правдоподобных статистических критериев Cr.

Вероятность ошибки второго рода обозначается β, а величина P{Θ_β}=1-β называется мощностью критерия. Чем больше эта мощность, тем меньше вероятность совершить ошибку второго рода.

В задачах статистического моделирования обычно устанавливают некоторое значение α, и статистический критерий Cr выбирают так, чтобы минимизировать β.

Обычная процедура проверки гипотез заключается в следующем: 1) по выборочным данным рассчитывается критерий проверки; 2) полученное значение критерия сравнивают с критическим значением, находимым из таблиц. Критическое значение каждого конкретного критерия определяется уровнем значимости и числом степеней свободы, по которому были рассчитаны величины, входящие в критерий.

Таблицы критических значений имеются в многочисленных книгах по статистике и

теории эксперимента.

 

27. Проверка значимости коэффициентов регрессии и адекватности статистической модели, полученной при ДФЭ.

Общая последовательность анализа экспериментальных данных:

1. Построить матрицу планирования ДФЭ 2^4-1 в некодированных и кодированных величинах.

2. Для приведенных экспериментальных данных рассчитать коэффициенты регрессии линейного полинома.

3. Проверить однородность выборочных дисперсий по критерию Кохрена.

4. Рассчитать дисперсию воспроизводимости.

5. Определить значимость коэффициентов регрессии.

6. Проверить адекватность статистической модели, используя результаты проведенных параллельных опытов.

Если в дополнение к столбцам x₁, x₂, x₃ вычислить столбцы для взаимодействий, то окажется (матрица I) столбец х₁ совпадает со столбцом х₂, столбец х₂ – со столбцом х₁х₃, столбец х₁х₂х₃ со столбцом х₀ х₃ (столбцы х₁х₃, x₂x₃, х₁х₂х₃ введены в матрицу ДФЭ 2^3-1 для пояснения).

Таким образом, сокращение числа опытов приводит к появлению корреляции между некоторыми столбцами матрицы планирования, что не позволяет раздельно оценивать эффекты факторов и эффекты взаимодействия, и, следовательно, оценки получаются смешанными (оценки в которых учитываются линейные эффекты и эффекты взаимодействия).

По данному плану (матрица I) можно выразить коэффициенты

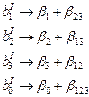
где буквами греческого алфавита обозначены коэффициенты регрессии генеральной совокупности (математические ожидания соответствующих коэффициентов), а буквами латинского алфавита – их оценки. Можно реализовать и другую полуреплику, где х₃ = – х₁х₂ (матрица II, таблица).

По матрице II смешанные оценки коэффициентов регрессии будут

В процедуру проверки значимости коэффициентов регрессии входит:

а) вычисление дисперсий коэффициентов регрессии 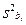, которые при факторном планировании первого порядка для всех коэффициентов регрессии равны и минимальны, по формуле:

где N – число опытов в матрице планирования;

б) составление отношений:

здесь

и сравнение их со значением t-критерия, которое находят по таблицам распределения Стьюдента для выбранного уровня значимости p (например, p =0,05) и числа степеней свободы v=N^*·(m–1), то есть

Если условие выполняется, то проверяемый коэффициент регрессии значимый и, наоборот.

В практических расчетах для проверки значимости коэффициентов b_i наиболее часто используют следующие выражения:

где Db_i – доверительный интервал для коэффициента – тот интервал, в пределах которого коэффициент, в действительности равный нулю, может отклониться от истинного значения c заданной малой вероятностью;

t – находят по таблицам критерия Стьюдента для выбранного уровня значимости и числа степеней свободы v=N^*.

Если его абсолютное значение коэффициента регрессии превышает величину абсолютного значения отклонения , тогда коэффициент регрессии значим.

Чтобы проверить гипотезу об адекватности математической модели используют критерий Фишера:

Остаточная дисперсия вычисляется по формуле:

где v=(N–l–1) – число степеней свободы; N – количество опытов (число строк в матрице плана); l – число значимых коэффициентов регрессии.

где F_кр – критическое значение критерия Фишера для выбранного уровнязначимости (p=0,05) и степеней свободы числителя v₁ = N–l–1 и знаменателя v₂ = N^*(т–1), N^* – количество групп параллельных опытов.

При соблюдении условия считают, что полученное уравнение регрессии адекватно.

 

15. Критерий исключения грубой ошибки.

Часто возникает вопрос о том, следует ли отвергать некоторые результаты эксперимента, резко отличающиеся от остальных. Если эти результаты получены из-за грубой ошибки, то их необходимо отбросить, не подвергая никаким статистическим оценкам. В противном случае необходимо произвести проверку резко выделяющихся значений.

Поэтому нуль-гипотеза имеет вид: подозрительный результат относится к той же генеральной совокупности, что и остальные. Альтернативная: этот результат порожден грубой ошибкой и должен быть исключен из дальнейшей обработки данных.

Критерий проверки r имеет вид

 

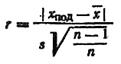где x_под – «подозрительный» результат (наибольший или наименьший);

– среднее, полученное по формуле;

S – среднеквадратичное отклонение; при этом в расчет х и S включается «подозрительный» результат;

n – количество измерений.

Полученное значение критерия сравнивают с табличным, полученным при заданных значениях уровня значимости α и числа степеней свободы v=n-1. Если полученное значение r больше значения, соответствующего табличному r_кр при данном n с заданным уровнем значимости, например, 0,05, то исследуемое наблюдение следует отбросить, если r< r_кр, то его следует оставить.

Критерий Фишера F. Прежде чем сравнивать средние значения двух выборок, необходимо убедиться в равенстве их дисперсий. При нормальном законе распределения СВ для проверки гипотезы о равенстве (однородности) выборочных дисперсий в качестве критерия используется статистика, которая равна отношению двух независимых оценок дисперсий генеральной совокупност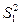и и 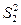, имеющих степень свободы соответственно v₁ и v₂, т.е.

При этом должно выполняться условие , где – большая величина выборочной дисперсии в двух выборках.

Найденное значение сравнивается с табличным при заданном уровне значимости p и степенях свободы v₁=n₁–1 и v₂=n₂-1. Если F<F_кр, тогда гипотеза о равенстве выборочных дисперсий принимается. Критерий Стьюдента t. Для проверки гипотезы о равенстве двух выборочных средних значений СВ, имеющей нормальный закон распределения, используют критерий Стьюдента t.

Нуль-гипотеза здесь: средние значения в двух сериях измерений являются оценками одного и того же генерального значения (математического ожидания, истинного значения).

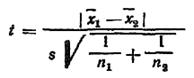Если серии измерений, в которых получены средние, сделаны с разной точностью (с разными дисперсиями), то процедура сравнения средних резко усложняется. В этих случаях можно рекомендовать специальные методы. Если дисперсии однородны и найдена общая оценка, тогда проверка проводится по критерию Стьюдента

 

где п₁ и n₂ – числа измерений в первой и второй сериях; s – единая оценка стандартного отклонения по всей совокупности измерений.

Критическое значение t зависит от v и α.

 

29.Планы второго порядка. Центральные композиционные планы.Статистический анализ уравнения регрессии для планов второго порядка.

Область близкую к экстремуму функции отклика (область оптимума) называют почти стационарной областью. Для описания этой области применяют полиномы вида

при этом количество необходимых опытов резко увеличивается при возрастании числа членов аппроксимирующего полинома.

В этой связи, имеются хорошо разработанные планы второго порядка, например центральное композиционное ротатабельное планирование (ЦКРП).

Центральным план называют вследствие симметричности относительно центра плана (точки, в которой все кодированные факторы x_u равны нулю); композиционным – потому, что они компонуются путем добавления определенного числа опытов к плану 1-го порядка, например плану ПФЭ.

α – звездное плечо.

Рисунок – Расположение опытных точек в плане 2-го порядка

При построении ЦКП к точкам плана ПФЭ добавляются точки в центре плана (центральные точки – одна или несколько параллельных) и точки, расположенные на всех осях координат на одинаковых расстояниях ±α от центра (звездные точки). Величину α называют звездным плечом. Для разных вариантов планов звездное плечо может быть разным.

Для двух факторов матрица такого плана имеет вид:

Планы второго порядка в строгом смысле не ортогональны. Специальный подбор величины α и добавочное преобразование переменных позволяют получить ортогональность и избавиться от взаимной корреляции коэффициентов при квадратах факторов.

Дисперсию воспроизводимости определяют по опытам в центре плана:

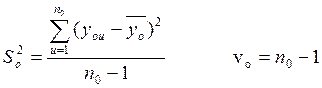где y_0u – значения отклика, полученное по опытам в центре плана, 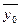– среднее значение отклика, полученное в центре плана; n₀ – число нулевых точек; v₀ – число степеней свободы дисперсии воспроизводимости.

Для проверки значимости коэффициентов регрессии вычисляют:

1) дисперсию коэффициентов уравнения регрессии по следующим формулам:

где a₁, a₃, a₄, a₅, a₆ – значения констант, согласно справочным данным (см. приложение);

2) составляют отношения

здесь

и сравнивают их со значением t-критерия, которое находят по таблицам распределения Стьюдента для выбранного уровня значимости p (например, p =0,05) и числа степеней свободы v=v₀, то есть

Если условие выполняется, то проверяемый коэффициент регрессии значим и, наоборот. Если один из квадратичных эффектов оказался незначимым, после его исключения следует пересчитать уравнение регрессии.

Проверку адекватности уравнения регрессии проводят по критерию Фишера:

где 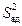– дисперсия адекватности, которая определяется из соотношения:

число степеней свободы дисперсии адекватности

Остаточную дисперсию рассчитывают по формуле:

где – экспериментальные и расчетные согласно модели значения отклика; N – количество опытов; l – число значимых коэффициентов в уравнении регрессии. Уравнение адекватно, если F < F_кр. F_кр – табличное значение критерия Фишера для выбранного уровня значимости и числа степеней свободы числителя v_ад=v₁ и знаменателя v₀=v₂.

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: