 |
Зависимые и независимые случайные величины. Корреляция случайных величин. Корреляционное отношение и его свойства.
|
|
|
|
Корреляционная связь, или корреляция – связь случайных величин (СВ), носит вероятностный характер, т. е. одному значению одной случайной величины может соответствовать несколько разных значений другой случайной величины.
В технологии силикатных материалов часто приходится иметь дело с корреляционной связью между параметрами. Примерами корреляционной связи могут служить зависимости прочности стекла от его состава, температуры стекломассы от расхода газа и соотношения газ–воздух.
Уравнения функциональной связи широко используются в расчетах. Однако следует иметь в виду, что функциональные зависимости дают идеализированное представление об объекте исследования, т. к. не учитывают возможное влияние неконтролируемых переменных, неоднородность объектов исследования и погрешность при проведении измерений. Поэтому взаимосвязь исследуемых величин всегда имеет вероятностный характер.
Наиболее простой случай вероятностной связи представляет корреляция двух факторов – парная корреляция. Наглядное представление о такой связи дает корреляционное поле. При его построении данные опытов изображают точками, координаты которых соответствуют значениям двух случайных величин.
Взаимосвязь факторов тем больше, чем теснее расположены точки корреляционного поля около некоторой прямой или «плавной» кривой, представляющей собой аналитическую функцию, аппроксимирующую (приближенно описывающую) наблюдаемые данные, которая называется функцией регрессии. Если все точки корреляционного поля попадут на эту линию, то теснота связи окажется наибольшей и связь факторов будет функциональной. На рисунке приведены корреляционные графики для двух величин xи y.
|
|
|
Теснота корреляционной связи определяется коэффициентом корреляции r. Коэффициент корреляции r может принимать значения от –1 до +1. При r =±1 одна из величин х или у является линейной функцией второй.
 |
а) – положительная корреляция; б) – сильная положительная корреляция;
в) – слабая отрицательная корреляция; г) – некоррелированные случайные величины
Рисунок – Поле корреляции случайной величины
При r =0 корреляционная связь отсутствует. При r ≠0 могут существовать иные формы зависимости между xи y, отличные от корреляции; но если обе величины имеют нормальный закон распределения, то отсутствие корреляции означает их независимость
Если r > 0, то между случайными величинами прямая связь, т. е. с увеличением одной случайной величины увеличивается значение другой, например, высокая положительная корреляция между содержанием в рудах цинка и галлия указывает, что при увеличении содержания цинка в руде будет повышаться содержание галлия. При r < 0 – с увеличением одной случайной величины уменьшается значение другой.
Если мерой тесноты связи при линейной ее формеслужит линейный коэффициент корреляции,то для криволинейной зависимоститакой мерой служит корреляционное отношение.
Корреляционное отношение имеет разные значения для корреляционной связи y = f (x) и для связи x = f (y). Прямое корреляционное отношение (у/х) вычисляется по формуле

где yu / xu – точка эмпирической линии регрессии; N – число экспериментов;  – отклонения точек эмпирической линии регрессии от общего среднего по
– отклонения точек эмпирической линии регрессии от общего среднего по  .
.
Обратное корреляционное отношение х / у для малых выборок вычисляется по формуле

где – 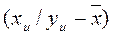 – отклонения точек эмпирической регрессии от общей средней по
– отклонения точек эмпирической регрессии от общей средней по  ;
;  – отклонения индивидуальных вариант в выборке от общего среднего по
– отклонения индивидуальных вариант в выборке от общего среднего по  .
.
Основные свойства корреляционного отношения.
|
|
|
корреляционное отношение всегда положительно и изменяется в пределах 0<  <1. При этом, если между у и х нет корреляционной связи, то
<1. При этом, если между у и х нет корреляционной связи, то  = 0, а если у связано с х функциональной связью, то
= 0, а если у связано с х функциональной связью, то  = 1;
= 1;
корреляционное отношение всегда не меньше численного значения
соответствующего коэффициента корреляции, т. е.  <=| R |;
<=| R |;
если  y/x = | R |, то регрессия у на х точно линейна; если
y/x = | R |, то регрессия у на х точно линейна; если  = | R |, то регрессия х на у точно линейна;
= | R |, то регрессия х на у точно линейна;
корреляционные отношения  y / x и
y / x и  х / у обычно не равны между собой; однако, чем больше связь между х и у приближается к прямолинейной, тем ближе по величине
х / у обычно не равны между собой; однако, чем больше связь между х и у приближается к прямолинейной, тем ближе по величине  y / x и
y / x и  х / у .
х / у .
Коэффициент корреляции (r) характеризует только линейную связь, а корреляционное отношение – любую форму связи.
При строго линейной связи  y / x =
y / x =  х / у = | r |. Следовательно, по разности между этими показателями можно судить о форме корреляционной зависимости между x и y.
х / у = | r |. Следовательно, по разности между этими показателями можно судить о форме корреляционной зависимости между x и y.
|
|
|


