Нуль и альтернативная гипотезы. Ошибки первого и второго рода. Способы уменьшения ошибок. Уровень значимости. Проверка гипотезы о нормальности закона распределения случайной величины.

Перенос знаний от выборочной совокупности к генеральной может быть осуществлен лишь с некоторой вероятностью P{Θ}, т.е. суждение о генеральной совокупности носит вероятностный характер и содержит элемент риска (1-P{Θ}). Суждения о свойствах генеральной совокупности называются статистическими гипотезами. Их проверка осуществляется с помощью статистических критериев, назначаемых в зависимости от формулировки гипотезы H.

Основная выдвинутая гипотеза называется нуль-гипотеза (H₀). Противоречащие ей гипотезы H_i называют альтернативными, или конкурирующими.

Нуль-гипотеза Н₀: между обеими выборками нет существенной разницы, обе они принадлежат одной генеральной совокупности, а имеющиеся различия обусловлены случайным характером выборок, например, влиянием случайных ошибок. В этом случае любые оценки, рассчитанные по этим двум выборкам, будут оценками одних и тех же генеральных (истинных) значений; тогда в большинстве случаев имеет смысл объединить обе выборки в одну, увеличив тем самым число степеней свободы.

Противоположная, или альтернативная гипотеза H₁ различия объясняются не случайностью, а существом дела. Выборки относятся к разным генеральным совокупностям.

Поскольку проверка гипотез ведется по выборке, то могут возникнуть ошибки двух родов. Если будет отвергнута правильная гипотеза, то совершается ошибка первого рода, если будет допущена неправильная гипотеза, то совершается ошибка второго рода.

Вероятность допустить ошибку первого рода называется уровнем значимости и обозначается α. Область, отвечающая вероятности α, называется критической, а дополняющая ее область, вероятность попадания в некоторую P{Θ_α}=1-α, называется областью правдоподобных статистических критериев Cr.

Вероятность ошибки второго рода обозначается β, а величина P{Θ_β}=1-β называется мощностью критерия. Чем больше эта мощность, тем меньше вероятность совершить ошибку второго рода.

В задачах статистического моделирования обычно устанавливают некоторое значение α, и статистический критерий Cr выбирают так, чтобы минимизировать β.

Обычная процедура проверки гипотез заключается в следующем:

1) по выборочным данным рассчитывается критерий проверки;

2) полученное значение критерия сравнивают с критическим значением, находимым из таблиц. Критическое значение каждого конкретного критерия определяется уровнем значимости и числом степеней свободы, по которому были рассчитаны величины, входящие в критерий.

Критерий Пирсона χ². Для проверки гипотезы о соответствии эмпирического распределения СВ теоретическому наиболее часто применяют критерий Пирсона χ². Суть этой проверки сводится к следующему. Предположим, что за время испытаний t выборки объемом n отказало d изделий, причем отказы фиксировались в различные моменты времени испытаний.

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что СВ d имеет данный закон распределения заданный функцией F(d) или плотностью вероятности f(d). Назовем этот закон распределения «теоретическим».

Зная этот закон, можно вычислить ожидаемое число отказов изделия в определенных интервалах, на которые разбить время испытания.

В результате получим теоретический ряд частот в k интервалах времени испытаний:

Подсчитаем также число отказавших изделий в этих же интервалах в нашем опыте и получим экспериментальный ряд частот

Для проверки согласованности теоретического и экспериментального распределений подсчитывается мера расхождения χ².

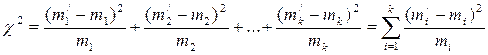
и число степеней свободы v=k–f, где f – число ограничений. Число ограничений равно числу параметров распределения, увеличенному на единицу. Так, например, для нормального закона распределения имеет места два параметра распределения (математическое ожидание и среднеквадратичное отклонение). Для распределения Пирсона составлены специальные таблицы. Пользуясь этими таблицами, можно для каждого значения критерия Пирсона и числа степеней свободы v определить вероятность P того, что за счет случайных причин мера расхождения теоретического и эмпирического распределений будет не меньше, чем фактически наблюдаемое в данной серии опытов значение χ².

Если эта вероятность сравнительно велика (P≥0,05), то можно признать гипотезу о соответствии эмпирического распределения теоретическому правильно.

Если вероятность весьма мала (P<0,05), т.е. событие с такой вероятностью можно считать практически невозможным, то результат опыта следует считать противоречащим гипотезе о том, что закон распределения величины x (в нашем случае x=d) есть F(x).

Следовательно, гипотеза отвергается и следует подобрать другую теоретическую кривую.

Критерий Колмогорова λ. Критерий Пирсона применяют только в тех случаях, когда число наблюдений (n≥25). Если теоретические значения параметров распределения известны, то лучшим критерием является критерий Колмогорова.

Для расчета критерия Колмогорова, как и для критерия Пирсона определяют теоретический m_i и экспериментальный ряд частот m_i^/. Затем рассчитывают накопленные суммы, которые образуются путем прибавления последующих частот к сумме предыдущих. Составляют разность между накопленными теоретическими и эмпирическими суммами и находят максимальное значение этой разности, вычисляя величину D по формуле:

Где , – разность функций экспериментального и теоретического распределения СВ.

Коэффициент λ находят по формуле:

.Пользуясь табличными данными для вычисленного значения λ, определяют вероятность P(λ) – вероятность того, что гипотетическая функция выбрана правильно.