 |
Экспериментальное изучение распределения времени пребывания элементов потока. Интегральная и дифференциальная функции распределения времени пребывания элементов потока
|
|
|
|
В аппаратах химической технологии в результате действия кинетических, гидродинамических, а также факторов теплообмена и массообмена в общем случае имеет неравномерность распределения частиц потока во времени, как по сечению потока, так и вдоль потока, вследствие поперечного и продольного перемешивания.
При этом степень неравномерности потока характеризует структуру среды и структуру потока.
Степень неравномерности распределения частиц в потоке во времени можно оценить по распределению вещества или по концентрации вещества в потоке. Отсюда задача отыскания структуры среды сводится к отысканию кривой на выходе из аппарата, в виде изменения концентрации во времени после внесения возмущения в поток на его входе. Возмущающим воздействием может быть введение в аппарат вместе с поступающим потоком какого-либо вещества (индикатора, трассера), кот. не реагирует со средой (наибольшее распространение получили ступенчатые и импульсные сигналы).При этом реакция объекта определяется фиксированием изменений во времени содержанием индикатора в потоке на выходе из аппарата, что позволяет дать оценку структуры потока и определить модель для этого потока. В качестве индикаторов используют подкрашенные инертные газы или жидкости, растворы солей флуарисцирующие примеси, радиактивные изотопы при соблюдении обязательного требования, чтобы они не претерпевали физико-химических изменений в потоке.
В химической технологии реакции объектов на стандартные входные сигналы (ступенчатый и импульсный) имеет специальное название. При стандартном ступенчатом сигнале на входе функция отклика на выходе представляет собой зависимость, которую называют F кривой (Fкр) или интегральной кривой.
|
|
|
Графики
Графическое изображение F кривой представляют в безразмерных координатах. Для этого концентрацию индикатора в потоке на выходе относят к его начальной концентрации С0 и откладывают по оси ординат значение Fкр = C/C0, а также используют понятие безразмерного времени
Θ = t/τ,
где t – натуральное время, τ – среднее время пребывания частиц в аппарате (τ = V/ν, где V – объем аппарата, ν – объемный расход жидкости).
Типичная форма отклика изображена на рисунке.
При импульсной подаче трассера на входе системы получается С кривая (импульсная характеристика) по координатным осям в которой обычно строят С кривую аналогично предыдущему случаю откладывая в безразмерных единицах. При этом условная площадь ограниченная С кривой равняется 1. По форме С и F кривые определяют структуру потока в аппарате.
Связь между дифференциальной и интегральной кривой определяется соотношением:
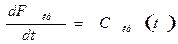
Метод установления модели потока на основе информации о его структуре состоит в том, что фиксируют реакцию объекта на выходе и затем получают выходные кривые, сравнивают с аналогичными кривыми типовых моделей. По результатам совпадений или отклонений дают оценку структуре исследуемого потока и строят модель отражающую гидродинамику данного потока.
41. Модель идеального перемешивания.
Согласно этой модели принимается,поступающий в аппарат поток мгновенно распределяется по всему объему. Вследствие полного перемешивания частиц потока. При этом концентрация распределенного вещества во всех точках зоны идеального перемешивания и в потоке на входе и выходе из него одинаково.
Рис.-Схематическое изображ. аппарата со структурой потока
Ур-е модели идеального перемешивания в диф.виде запишется следующим образом
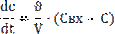
Начальные условия t=0,Ct=0=C0,где Свх иСвых=С концентр.в-ва в потоке соответственно на входе,выходе и в любой точке объема аппарата,моль/м3;t- время,с; 
-объемная скорость потока,поступающего в зону идеального перемешивания и выходящего из него,м3/с;V-объем зоны идеальноо перемешивания,м3
|
|
|
Модель МИС это модель сосредоточенными параметрами.Если учесть,что среднее время пребывания элемента потока в аппарате (обозначенное t=V/ 
),тогда модель будет представлена
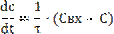
Для нахождения решения ур-я воспульзуемся преобразованием временной ф-ци по с(t) по Лаплассу.Принимая,что с(t)=Свых(t) и пользуясь соответствующими правилами,запишем операторное ур-е,которое соответствует решаемому
Или W(p)=Cвых(p)/Cвх(p)=1/ 
(1)
Это выражение(1) является операторным ур-ем модели идеального перемешивания.Поскольку величина V/ имеет смысл постоянной времени объекта T,тогда ур-е следует записать
W(p)= 1/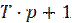 
Данное ур-е это передаточное ф-ция характеризующая модель идеального перемешивания.Для получения решения исходного диф-гоур-я в области действительной переменной проводят обратное преобразование по Лаплассу.
Cвых(t)=L-1(W(p) 
Свх(p))
Решение находят для двух характерных случаев:
Если Cвых(t)=Fкр,когдаСвх(t)=1(t) или Cвх(p)=1(p)(ступенчатые сигналы). И Cвых(t)=Скр,когдаСвх(t)= 
(t) или Cвх(p)=1(мпульсный сигнал)
Тогда для модели идеального смешения решения имеют вид
--при ступенчатом сигнале на входе
--при импульсном сигнале на входе
Графическая интерпритация
Рис.-Fкр-МИС
Рис.С-кривая-МИС
Как следует из вида кривых, а так же выражение для придаточной ф-ции,модели идеального смешения соотв.инерционное звено 1-го порядка.В целом МИС соответствует реальным потокам в проточных аппаратах с мешалкой,высота которой мало отличается от диаметра.Мешалка создает высокую степень перемешивания,а объемная скорость потока невелика.
|
|
|
