Главная | Обратная связь | Поможем написать вашу работу!

Тема Линейная алгебра: решение систем линейных уравнений.

Система из n линейных уравнений с n неизвестными

может быть записана в матричном виде AХ = В, где

– матрица коэффициентов системы,

– матрица-столбец неизвестных,

– матрица-столбец свободных членов системы,

Система из n уравнений с n неизвестными имеет единственное решение только в том случае, если главный определитель системы

Методы решения систем линейных уравнений.

Формулы Крамера

, i = 1,2,…,n

где - дополнительный определитель матрицы, отличающейся от матрицы A тем, что в ней столбец с номером i заменен на столбец В.

Возможные случаи:

	Система имеет единственное решение	Система совместна и определена
	Хотя бы один . Система не имеет решений.	Система несовместна
Все . Система имеет бесконечное множество решений.	Система совместна, но неопределена

При помощи обратной матрицы.

где - матрица, обратная к .

Метод Гаусса.

Метод Гаусса или метод последовательного исключения неизвестных заключается в том, чтобы с помощью элементарных преобразований привести расширенную матрицу системы

к ступенчатому виду (получить нули под главной диагональю)

после чего осуществить обратный ход: по матрице, приведенной к ступенчатому виду составить систему уравнений и решить ее.

Элементарные преобразования матрицы:

1) перестановка строк;

2) умножение строки на число, отличное от нуля;

3) сложение строки с другой строкой, умноженной на число.

Тема Аналитическая геометрия

Расстояние между двумя точками А(х_А; у_А) и В(х_В; у_В):

(1)

Деление отрезка в заданномотношении.

Если точка С делит отрезок АВ в отношении λ, начиная от точки A, т.е. , то координаты точки C:

(2)

Если точка С делит отрезок АВ пополам, т.е. =1, то координаты точки C:

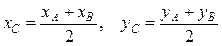(3)

Уравнение прямой на плоскости.

1) Общее уравнение прямой:

(4)

2) Уравнение прямой с угловым коэффициентом:

(5)

3) Уравнение прямой с угловым коэффициентом, проходящей через заданную точку :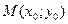

(6)

4) Уравнение прямой, проходящей через две точки и :

(7)

5) Уравнение прямой в отрезках:

(8)

Пусть на плоскости заданы две прямые:

Условие параллельности прямых на плоскости:

(9)

Условие перпендикулярности прямых:

(10)

Тангенс острого угла между пересекающимися прямыми можно найти по формуле:

, (11)

откуда .

Уравнение плоскости в пространстве

1) Общее уравнение плоскости:

(12)

2) Уравнение плоскости, проходящей через точку перпендикулярно вектору :

(13)

Вектор называется нормальным вектором плоскости.

3) Уравнение плоскости, проходящей через три заданные точки :

(14)

4) Косинус угла между двумя плоскостями, заданными уравнениями и вычисляется как косинус угла между нормальными векторами заданных плоскостей:

(15)

Уравнение прямой в пространстве

1) Каноническое уравнения прямой:

(16)

Вектор называется направляющим вектором прямой, он параллелен данной прямой.

2) Уравнение прямой, проходящей через две точки и :

(17)

3) Косинус угла между двумя прямыми вычисляется как косинус угла между направляющими векторами данных прямых:

(18)

4) Условие перпендикулярности прямых:

, (19)

где , – направляющие векторы данных прямых.

Кривые второго порядка: эллипс, гипербола, парабола

Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Рисунок 1.

– фокусы, – половина расстояния между фокусами.

Каноническое уравнение эллипса:

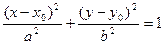(20)

– большая полуось эллипса, – малая полуось эллипса, – центр эллипса

Для эллипса справедливо: c ² = a ²– b ².

Число называется эксцентриситетом эллипса .

Если центр эллипса лежит в начале координат, то его уравнение примет вид:

(21)

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Рисунок 2.

Каноническое уравнение гиперболы:

(22)

– действительная полуось гиперболы, – мнимая полуось гиперболы, – центр гиперболы. и образуют основной прямоугольник гиперболы.

Для гиперболы справедливо: c ² = a ²+ b ².

Число называется эксцентриситетом эллипса .

Уравнения асимптот гиперболы:

Если центр гиперболы лежит в начале координат, то его уравнение примет вид:

(23)

Параболойназывается множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директрисой.

Расстояние от фокуса до директрисы называется параметром параболы.

Рисунок 3.

Каноническое уравнение параболы

(24)