 |
Дифференциальные уравнения 2-го порядка
|
|
|
|
Дифференциальным уравнением 2-го порядка называется уравнение вида
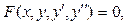 (53)
(53)
где х – независимая переменная, y – неизвестная функция этой переменной,  и
и  – ее производные.
– ее производные.
Общее решение уравнения 2-го порядка имеет вид:
y = g (x, C 1, C 2), (54)
где С 1 и С 2 – две произвольные постоянные.
Задача Коши для дифференциального уравнения 2-го порядка (53) состоит в нахождении частного решения уравнения, удовлетворяющего двум начальным условиям  . Для решения задачи Коши нужно подставить в общее решение (54) и его производную заданные начальные условия, решить полученную систему двух уравнений относительно неизвестных С 1 и С 2 и подставить найденные значения постоянных в общее решение.
. Для решения задачи Коши нужно подставить в общее решение (54) и его производную заданные начальные условия, решить полученную систему двух уравнений относительно неизвестных С 1 и С 2 и подставить найденные значения постоянных в общее решение.
Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
Уравнение
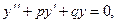 (55)
(55)
где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.
Общее решение уравнения (55) имеет вид:  ,
,
где у 1 и у 2 – два линейно независимых частных решения этого уравнения, С 1 и С 2 – произвольные постоянные.
Для нахождения линейно независимых частных решений у 1 и у 2 используется характеристическое уравнение вида
 . (56)
. (56)
В зависимости от корней характеристического уравнения получаются различные виды функций у 1 и у 2 и вид общего решения уравнения (таблица 6).
Таблица 6.
| Дискриминант характеристического уравнения | Корни характеристического уравнения | Вид общего решения уравнения |

| действительные
различные 
| 
|

| действительные
равные 
| 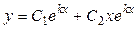
|

| комплексные 
| 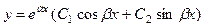
|
Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
|
|
|
Уравнение вида
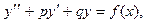 (57)
(57)
где p и q – действительные числа, называется линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.
Общее решение линейного неоднородного уравнения (57) имеет вид:
 (58)
(58)
где  – общее решение соответствующего однородного уравнения (55), а
– общее решение соответствующего однородного уравнения (55), а  – частное решение неоднородного уравнения (57).
– частное решение неоднородного уравнения (57).
Построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение соответствующего однородного уравнения  , затем найти частное решение
, затем найти частное решение  неоднородного уравнения.
неоднородного уравнения.
Для нахождения частного решения  уравнения можно использовать метод неопределенных коэффициентов.
уравнения можно использовать метод неопределенных коэффициентов.
1) Если  , то частное решение можно искать в виде:
, то частное решение можно искать в виде:
 (59)
(59)
где k 1, k 2 – корни характеристического уравнения, Qn (x) – многочлен степени n.
2) Если  , то частное решение
, то частное решение  можно искать в виде:
можно искать в виде:
 (60)
(60)
где k 1, k 2 – корни характеристического уравнения, А и В – неизвестные постоянные.
Тема Ряды
Числовым рядом называется выражение вида
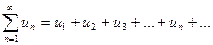 , (61)
, (61)
где u1, u2, u3,…, un,… - действительные или комплексные числа, называемые членами ряда. un – общий член ряда.
Ряд считается заданным, если известен общий член ряда  .
.
Сумма первых n членов ряда называется n -ной частичной суммой ряда и обозначается Sn.
 (62)
(62)
Предел последовательности  частичных сумм ряда (61) при
частичных сумм ряда (61) при  , если он существует, называется суммой ряда, т.е.
, если он существует, называется суммой ряда, т.е. 
Если  существует, то ряд (61) сходится. В противном случае ряд (61) расходится.
существует, то ряд (61) сходится. В противном случае ряд (61) расходится.
Необходимый признак сходимости
Если ряд
 сходится, то его общий член
сходится, то его общий член  при
при  стремится к нулю, т.е.
стремится к нулю, т.е.  .
.
Достаточные признаки сходимости знакоположительных рядов
Знакоположительным называется ряд с неотрицательными членами.
Первый признак сравнения.
Пусть даны два ряда с положительными членами:
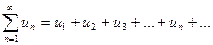 (63)
(63)
и
 , (64)
, (64)
причем 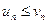 ,
,  Тогда если сходится ряд (64), то сходится и ряд (63); если расходится ряд (63), то расходится и ряд (64).
Тогда если сходится ряд (64), то сходится и ряд (63); если расходится ряд (63), то расходится и ряд (64).
|
|
|
Второй признак сравнения (в предельной форме).
Пусть для рядов (63) и (64) существует предел
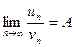 .
.
Тогда если  , то либо оба ряда сходятся, либо расходятся одновременно; если
, то либо оба ряда сходятся, либо расходятся одновременно; если  и ряд (64) сходится, то сходится и ряд (63). Если же
и ряд (64) сходится, то сходится и ряд (63). Если же  и ряд (64) расходится, то расходится и ряд (63).
и ряд (64) расходится, то расходится и ряд (63).
Стандартные ряды, применяемые для признаков сравнения:
Гармонический ряд: 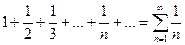 - расходится.
- расходится.
Обобщенный гармонический ряд (ряд Дирихле):  расходится при
расходится при  и сходится при
и сходится при  .
.
Ряд геометрической прогрессии  при
при  сходится, при
сходится, при  расходится.
расходится.
Признак Даламбера.
Пусть дан ряд с положительными членами  и существует конечный или бесконечный предел
и существует конечный или бесконечный предел
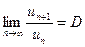 , (65)
, (65)
то этот ряд сходится при 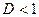 и расходится при
и расходится при  .
.
При  признак Даламбера не дает однозначного ответа о сходимости.
признак Даламбера не дает однозначного ответа о сходимости.
Радикальный признак Коши.
Пусть дан ряд с положительными членами  и существует конечный или бесконечный предел
и существует конечный или бесконечный предел
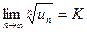 , (66)
, (66)
то этот ряд сходится, если  , и расходится, если
, и расходится, если 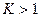 .
.
При  признак Коши не дает однозначного ответа о сходимости.
признак Коши не дает однозначного ответа о сходимости.
Интегральный признак Коши.
Если члены знакоположительного ряда  могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей при
могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей при  функции
функции  , то если сходится несобственный интеграл
, то если сходится несобственный интеграл  , то сходится и ряд (61). Если же интеграл расходится, то расходится и ряд (61).
, то сходится и ряд (61). Если же интеграл расходится, то расходится и ряд (61).
Знакочередующиеся ряды, их абсолютная и условная сходимости. Признак Лейбница.
Числовой ряд называется знакочередующимся, если он содержит как положительные, так и отрицательные члены, которые следуют друг за другом поочередно.
 (67)
(67)
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, и общий член ряда по модулю стремится к нулю.
Для сходимости знакочередующегося ряда (67) достаточно выполнения двух условий:
1) 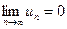 ;
;
2)  .
.
При этом, если ряд (67) сходится по признаку Лейбница и сходится ряд, составленный и модулей его членов
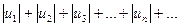 , (68)
, (68)
то говорят, что ряд (67) сходится абсолютно. Если же ряд (68) расходится, то ряд (67) сходится условно (может как сходиться, так и расходиться).
Функциональные ряды.
Ряд, членами которого являются функции от  , называется функциональным:
, называется функциональным:
 , (69)
, (69)
Значение 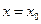 , при котором ряд (69) сходится, т.е. сходится числовой ряд
, при котором ряд (69) сходится, т.е. сходится числовой ряд  , называется точкой сходимости функционального ряда.
, называется точкой сходимости функционального ряда.
|
|
|
Множество значений аргумента  , при которых функции
, при которых функции 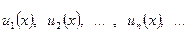 определены, и ряд
определены, и ряд  сходится, называется областью сходимости функционального ряда.
сходится, называется областью сходимости функционального ряда.
Функция  называется остатком функционального ряда.
называется остатком функционального ряда.
Степенные ряды. Радиус и область и сходимости степенного ряда.
Степенным рядом называется функциональный ряд вида
 , (70)
, (70)
где a, A0, A1, A2, …, An, … - действительные числа.Частный случай степенного ряда при  :
:
 .
.
Теорема Абеля. Если степенной ряд (14) сходится при  , то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству
, то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству
 (71)
(71)
Если же ряд (14) расходится при  , то он расходится и при любом x, удовлетворяющем неравенству
, то он расходится и при любом x, удовлетворяющем неравенству
 (72)
(72)
Из теоремы Абеля следует, что существует симметричный интервал абсолютной сходимости степенного ряда относительно точки  , которая называется центром сходимости. Половина длины интервала называется радиусом сходимости и обозначается R.
, которая называется центром сходимости. Половина длины интервала называется радиусом сходимости и обозначается R.
Радиус сходимости R может принимать значения  . Сходимость ряда в точках
. Сходимость ряда в точках  и
и 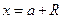 исследуется дополнительно и добавляется к интервалу, образуя область сходимости.
исследуется дополнительно и добавляется к интервалу, образуя область сходимости.
Радиус сходимости находится по формуле
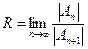 (73)
(73)
Или при применении радикального признака Коши:
 (74)
(74)
Ряды Тейлора и Маклорена.
Рядом Тейлора для функции  называется степенной ряд
называется степенной ряд
 (75)
(75)
Частным случаем ряда Тейлора при  является ряд Маклорена:
является ряд Маклорена:
 (76)
(76)
При разложении функций в ряд удобно применять ряды Маклорена для некоторых элементарных функций, представленные ниже:
 .
.

 .
.
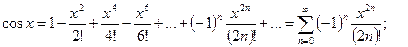
 .
. 
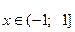 ;
;
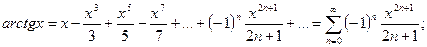
 .
.


 .
.
Последний ряд называется биномиальным, частные случаи которого представлены ниже:
 .
.

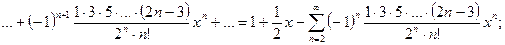
 .
.
Приложения степенных рядов для приближенного вычисления функций и определенных интегралов.
Для вычисления значения приближенного функции при данном значении аргумента можно воспользоваться разложением этой функции в степенной ряд, удобно воспользоваться разложениями в ряд Маклорена элементарных функций.
Для приближенного вычисления определенного интеграла нужно разложить в степенной ряд подынтегральную функцию, проинтегрировать степенной ряд почленно и сохранить в ряде достаточное количество его первых членов (для обеспечения заданной точности).
|
|
|
Вопросы к экзамену по дисциплине «Математика», 1 семестр
1. Вектор на плоскости. Сложение и вычитание векторов, умножение вектора на число в геометрической и координатной формах
2. Угол между векторами, косинус и синус угла. Признаки ортогональности и коллинеарности векторов.
3. Скалярное произведение векторов.
4. Вектор в п -мерном пространстве. Компланарность векторов. Необходимое и достаточное условие компланарности векторов в 3-мерном пространстве.
5. Матрицы. Виды матриц. Элементарные преобразования матриц.
6. Сложение матриц и умножение матрицы на число. Умножение матриц, возведение в степень.
7. Свойства определителей.
8. Миноры и алгебраические дополнения.
9. Вычисление определителей.
10. Определители n- го порядка. Критерий равенства определителя нулю.
11. Разложение определителя по элементам какого-либо ряда.
12. Алгоритм нахождения обратной матрицы.
13. Система линейных алгебраических уравнений (основные понятия).
14. Решение СЛАУ методом Крамера.
15. Решение СЛАУ методом Гаусса.
16. Матричный способ решения СЛАУ.
17. Прямоугольная система координат на плоскости.
18. Прямая на плоскости. Угловой коэффициент. Уравнения прямой с заданным угловым коэффициентом, проходящей через две точки, уравнение в отрезках.
19. Угол между прямыми на плоскости. Признаки параллельности и перпендикулярности прямых.
20. Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов.
21. Прямоугольная система координат в пространстве.
22. Общее уравнение плоскости в пространстве, геометрический смысл коэффициентов.
23. Нормированное уравнение плоскости. Геометрический смысл его левой части.
24. Уравнения прямой в пространстве, направляющий вектор. Углы между прямыми и плоскостями. Взаимное расположение плоскостей и прямых в пространстве.
25. Кривые второго порядка. Окружность.
26. Эллипс.
27. Гипербола.
28. Парабола.
29. Определение функции и её свойства. Способы задания функции.
30. Основные элементарные функции.
31. Предел последовательности.
32. Предел последовательности.
33. Ограниченность функции, имеющей предел. Бесконечно малые, их связь с функциями, имеющими предел. Теоремы о бесконечно малых и бесконечно больших.
34. Теоремы о пределах.
35. Замечательные пределы. Число е.
36. Список эквивалентных. Замена на эквивалентные при вычислении предела.
37. Класс элементарных функций, их непрерывность. Классификация точек разрыва функции.
|
|
|
38. Задачи, приводящие к понятию производной.
39. Производная, её геометрический смысл. Связь между дифференцируемостью и непрерывностью.
40. Линейные свойства производной. Производная суммы, произведения и частного.
41. Производная сложной и обратной функции.
42. Таблица производных
43. Уравнение касательной и нормали к графику функции.
44. Дифференциал, его геометрический смысл. Производная как отношение дифференциалов.
45. Локальный максимум и минимум. Экстремум. Необходимый признак экстремума (теорема Ферма). Задачи отыскания наибольшего и наименьшего значения функции.
46. Критерии возрастания, убывания, константы. Достаточный признаки экстремума по первой производной.
47. Основные теоремы дифференцирования.
48. Достаточный признак экстремума функции по второй производной.
49. Формула Тейлора. Разложение в ряд Тейлора элементарных функций.
50. Схема исследования и построения графика функции.
Вопросы к экзамену по дисциплине «Математика», 2 семестр
1. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Замена переменной интегрирования. Список формул интегрирования элементарных функций.
2. Интегрирование по частям. Интегралы от простейших рациональных функций.
3. Понятие определенного интеграла. Линейные свойства.
4. Формула Ньютона - Лейбница.
5. Интегрирование по частям и замена переменной в определенном интеграле.
6. Приложения определенного интеграла в геометрии и экономике.
7. Понятие несобственного интеграла.
8. Функция многих переменных. Линии и поверхности уровня.
9. Предел и непрерывность ФНП.
10. Частные производные.
11. Градиент функции. Производная по направлению.
12. Экстремум, необходимые и достаточные условия эктремума ФНП.
13. Понятие дифференциального уравнения. Порядок уравнения. Частные и общее решения.
14. ДУ первого порядка с разделяющимися переменными,
15. ДУ однородные первого порядка.
16. ДУ линейные первого порядка (метод Бернулли).
17. ДУ Бернулли.
18. Задача Коши. Теоремы существования и единственности решения для уравнений 1-го и 2-го порядка.
19. Линейные уравнения 2-го порядка.
20. Структура общего решения линейного однородного уравнения.
21. Уравнения с постоянными коэффициентами. Характеристическое уравнение. Общее решение в случае вещественных корней характеристического уравнения.
22. Характеристическое уравнение с комплексными корнями.
23. Алгоритм общего решения линейного неоднородного уравнения со специальной правой частью.
24. Решение неоднородных ДУ 2-го порядка с постоянными коэффициентами методом неопределенных коэффициентов.
25. Принцип наложения решений.
26. Понятие числового ряда.
27. Какой ряд называется сходящимся (расходящимся)?
28. Свойства сходящихся рядов.
29. Необходимый признак сходимости рядов.
30. Достаточный признак расходимости рядов
31. Признаки сравнения
32. Признак Даламбера.
33. Признак Коши.
34. Интегральный признак.
35. Ряды с членами произвольного знака.
36. Абсолютная сходимость.
37. Признак Лейбница.
38. Понятие степенного ряда.
39. Нахождение радиуса сходимости степенного ряда.
40. Ряд Тейлора и ряд Маклорена.
Методические указания к выполнению и оформлению контрольной работы:
1. В первом семестре выполняются контрольные работы №1 и №2. Во втором семестре выполняются контрольные работы №3 и №4.
2. В контрольной работе используются два параметра M и N. Параметр M равен предпоследней цифре номера зачетной книжки, а параметр N равен последней цифре. Например, для студенческого билета номер 147 N = 7, M = 4.
3. Контрольная работа оформляется в школьной тетради 18 страниц.
4. На титульном листе указываются значения параметров M и N. Решения задач должны следовать в том порядке, в каком они предложены.
5. Каждая задача должна начинаться с условия и заканчиваться ответом.
6. Решение каждой задачи должно сопровождаться подробными пояснениями.
Контрольная работа №1
Задача 1
Даны векторы a и b. Найти вектор c = 2 a - b, модуль вектора с, скалярное произведение (a, 2b), где a = {1, M+4, -1, N-5}, b = {-M+5, -1, 5 - N, 2}. 
Задача 2
1) Найти расстояние между точками А = (N+2, -M-1, N+M) и В = (M, N, M-N).
2) Найти точку пересечения прямых y=-(N+1)x+2 и y=(M+1)x-M-N.
3) Найти уравнение прямой, проходящей через точку (M+1; N+1) и перпендикулярной к прямой y=-2x-1.
4) Написать каноническое уравнение кривой, заданной уравнением  . Построить кривую.
. Построить кривую.
Задача 3
Даны матрица  размерностью
размерностью  и вектор-строка b. Найти произведения AT× b T и b × A;
и вектор-строка b. Найти произведения AT× b T и b × A; 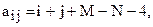 b = {M-5, 1, 4-N}.
b = {M-5, 1, 4-N}.
Задача 4
Даны матрицы 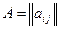 и
и  размерностью
размерностью  . Проверить, коммутативны ли матрицы Aи B,и найти определители матриц. Элементы матриц вычисляются по формулам:
. Проверить, коммутативны ли матрицы Aи B,и найти определители матриц. Элементы матриц вычисляются по формулам:  .
.
Задача 5
Решить систему из трех уравнений, пользуясь формулой Крамера и методом Гаусса:

Задача 6
Составить систему из двух уравнений с двумя неизвестными так, чтобы она:
a) имела единственное решение;
b) не имела решений;
с) имела бесконечно много решений.
Найти определители этих систем. Учитывая, что каждое из уравнений системы является уравнением прямой линии на плоскости, изобразить эти прямые и пояснить, что означает каждый из трех вариантов с точки зрения взаимного расположения прямых.
Задача 7
Найти пределы:
a)  ;
;
b)  ;
;
c)  ;
;
d) 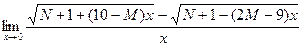 ;
;
e)  ];
];
f)  .
.
Контрольная работа №2
Задача 1
Найти производные функций:
a)  ; b)
; b)  ;
;
c)  ; d)
; d)  .
.
Задача 2
Найти вторую производную функции  .
.
Задача 3
Найти пределы, пользуясь правилом Лопиталя:
а)  ; b)
; b) 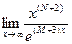 .
.
Задача 4
Исследовать функции и построить их графики:
a)  ; b)
; b)  .
.
Задача 5
Найти неопределенные интегралы:
a) 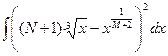
b) 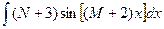
c) 
d) 
Контрольная работа №3
Задача 1
Найти определенные интегралы:
a) 
b) 
c) 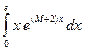
Задача 2
Найти площадь верхней полуволны синусоиды 
Задача 3
Найти первые частные производные функций:
a)  ;
;
b)  ;
;
c)  ;
;
d) 
Задача 4
Найти полные дифференциалы функций:
a)  ;
;
b)  ;
;
Задача 5
Найти градиент функции в точке ( ):
):
a) 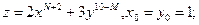
b) 
Задача 6
Исследовать на экстремум функцию:
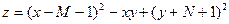 .
.
Контрольная работа №4
Задача 1
Найти общее решение дифференциальных уравнений и проверить правильность найденных решений дифференцированием:
a)  b)
b)  c)
c) 
Задача 2
Найти решения дифференциальных уравнений с разделяющимися переменными:
a) 
b) 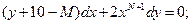
c) 
Задача 3
Найти решения линейных уравнений 1 порядка:
a) 
b)  , y=0 при x=1
, y=0 при x=1
Задача 4
Найти решения линейных однородных уравнений с постоянными коэффициентами:
a) 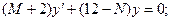
b) 
c) 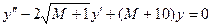 с условиями
с условиями  при x = 0;
при x = 0;
d) 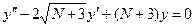 .
.
Задача 5
Найти решения линейных неоднородных уравнений с постоянными коэффициентами в виде суммы общего решения однородного уравнения и произвольного частного решения неоднородного уравнения:
a)  , y = 0 при x = 0;
, y = 0 при x = 0;
b) 
Задача 6
Исследовать сходимость следующих рядов:
а) 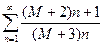 ; б)
; б) 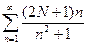 ; с)
; с) 
Задача 7
Найти область сходимости степенных рядов:
а) 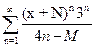 б)
б) 
Задача 8
Вычислить  с точностью до 0,001
с точностью до 0,001
|
|
|


