 |
Исследование функций и построение графиков
|
|
|
|
Исследование функций и построение ее графика производится по следующему плану:
1) Область определения функции
2) Четность функции, ее периодичность.
3) Точки разрыва функции
4) Промежутки возрастания и убывания функции, экстремумы.
Для определения промежутков монотонности функции используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
если на интервале 
производная 
сохраняет знак, то при 
функция 
возрастает, а при 
, то функция убывает.
Для установления точек экстремумов функции 
используют необходимый и достаточные признаки существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция имеет экстремум в точке 
, то ее производная в этой точке равна нулю или не существует.
Точки, принадлежащие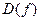 
, в которых производная 
равна нулю или не существует, называют критическими точками функции по ее первой производной (точками, «подозрительными на экстремум»).
Первый достаточный признак существования экстремума: если при переходе через критическую точку производная 
изменяет свой знак с плюса на минус, то точка есть точка максимума, если изменяет свой знак с минуса на плюс, то точка есть точка минимума.
Второй достаточный признак существования экстремума: если 
– дважды дифференцируемая функция в точке и 
, тогда: если 
, то – точка минимума функции, а если 
, то – точка максимума.
5) Промежутки выпуклости, вогнутости графика и точки перегиба.
График функции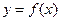 
называется выпуклым вниз (вогнутым) на интервале 
, если он расположен выше любой ее касательной на этом интервале. График функции 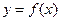называется выпуклым вверх (выпуклым) на интервале , если он расположен ниже любой ее касательной на этом интервале.
|
|
|
Точки графика, отделяющие участки выпуклости от участков вогнутости, называются точками перегиба.
Достаточное условие выпуклости и вогнутости графика функции: если функция является дважды дифференцируемой и ее вторая производная 
<0, то график функции на этом интервале выпуклый вверх. Если 
>0 – график выпуклый вниз (вогнутый).
Точки, принадлежащие графику функции 
, в которых 
или не существует, называются критическими точками функции по ее второй производной (точками, «подозрительными на перегиб»).
Достаточное условие для точек перегиба: если вторая производная 
при переходе через точку , подозрительную на перегиб, меняет знак, то точка с абсциссой х0 является точкой перегиба.
6) Асимптоты.
а) вертикальные
Прямая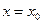 
является вертикальной асимптотой графика функции 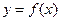, если функция имеет бесконечный разрыв в точке 
. Необходимо вычислить односторонние пределы функции в точках, ограничивающих промежутки ее .
б) наклонные
Если график функции 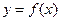имеет наклонную асимптоту, то ее уравнение будем искать в виде 
. Параметры k и b можно найти по формулам:
, 
(33)
Если хотя бы один из этих пределов является бесконечным или не существует, то наклонных асимптот нет. В случае, когда k = 0, график имеет горизонтальную асимптоту с уравнением y = b.
7) Дополнительные точки графика.
8) График.
Тема Интегральное исчисление функции одной переменной.
Неопределенный интеграл.
Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если для всех x из этого интервала выполняется равенство
(34)
Неопределенным интегралом от функции f(x) называется множество всех первообразных функции 
, и обозначается 
.
Операция интегрирования является обратной к операции дифференцирования.
Таблица 4.
Таблица интегралов
1. 
| 9. 
|
2. 
| 10. 
|
3. 
| 11. 
|
4. 
| 12. 
|
5. 
| 13. 
|
6. 
| 14. 
|
7. 
| 15. 
|
8. 
| 16. 
|
|
|
|
|
|
|
