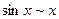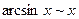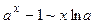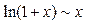|
Тема Функция. Предел и непрерывность функции.
|
|
|
|
Переменной называют величину 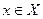 , принимающую значения из некоторого множества значений Х.
, принимающую значения из некоторого множества значений Х.
Если каждому значению переменной х из множества Х поставлено в соответствие по определенному правилу f единственное значение переменной у из множества Y, то говорят, что задана функция  , определенная на множестве Х с множеством значений Y.
, определенная на множестве Х с множеством значений Y.
При этом:
х – аргумент (независимая переменная);
у – значение функции (зависимая переменная);
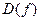 – область определения функции;
– область определения функции;
 – множество значений функции.
– множество значений функции.
Функция  , определенная на множестве
, определенная на множестве 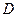 , называется четной, если область ее определения симметрична относительно начала координат и
, называется четной, если область ее определения симметрична относительно начала координат и 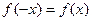 ,
,  . График четной функции симметричен относительно оси Oy.
. График четной функции симметричен относительно оси Oy.
Функция  , определенная на множестве
, определенная на множестве 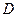 , называется нечетной, если область ее определения симметрична относительно начала координат и
, называется нечетной, если область ее определения симметрична относительно начала координат и 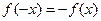 ,
,  . График нечетной функции симметричен относительно начала координат.
. График нечетной функции симметричен относительно начала координат.
Функция  , определенная на множестве
, определенная на множестве 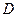 , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число  , что
, что  ,
,  .
.
Если 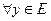 ставится в соответствие единственное значение
ставится в соответствие единственное значение  , то определена функция
, то определена функция  с областью определения
с областью определения 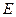 и множеством значений
и множеством значений 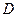 . Такая функция
. Такая функция 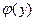 называется обратной к функции
называется обратной к функции  .
.
Функции  и
и  называются взаимно обратными функциями. Графики взаимно обратных функций симметричны относительно прямой у = х.
называются взаимно обратными функциями. Графики взаимно обратных функций симметричны относительно прямой у = х.
Функция  называется возрастающей на множестве
называется возрастающей на множестве 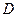 , если для любых значений
, если для любых значений 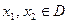 из неравенства
из неравенства 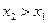 следует неравенство
следует неравенство  , то есть если большему значению аргумента из множества
, то есть если большему значению аргумента из множества 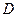 соответствует большее значение функции.
соответствует большее значение функции.
Функция  называется убывающей на множестве
называется убывающей на множестве 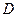 , если для любых значений
, если для любых значений 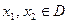 из неравенства
из неравенства 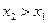 следует неравенство
следует неравенство 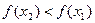 , то есть если большему значению аргумента из множества
, то есть если большему значению аргумента из множества 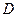 соответствует меньшее значение функции.
соответствует меньшее значение функции.
|
|
|
Промежутки возрастания и убывания функции называются промежутками монотонности функции.
Если функция  монотонна на множестве
монотонна на множестве 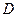 , то она имеет обратную функцию
, то она имеет обратную функцию 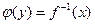 .
.
Точка х 0 называется точкой максимума функции  , если существует такая окрестность точки х 0, что для любой точки х ¹ х 0 этой окрестности выполняется неравенство
, если существует такая окрестность точки х 0, что для любой точки х ¹ х 0 этой окрестности выполняется неравенство 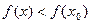 .
.
Если для любой точки х ¹ х 0 из некоторой окрестности точки х 0 выполняется неравенство  , то х 0 называется точкой минимума.
, то х 0 называется точкой минимума.
Точки максимумов и минимумов называются точками экстремумов функции, а значения y max и y min называются экстремумами функции.
Предел функции.
Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  .
.
Число А называется пределом функции  в точке
в точке  (или при
(или при 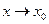 ), если для любого числа
), если для любого числа 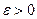 , можно указать такую окрестность
, можно указать такую окрестность  точки
точки  , что при всех
, что при всех  , принадлежащих этой окрестности, выполняется неравенство
, принадлежащих этой окрестности, выполняется неравенство  .
.
Предел функции обозначается  , или
, или 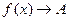 при
при 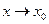 .
.
Если 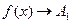 при
при 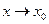 только при
только при 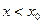 , то
, то  называется пределом функции
называется пределом функции  в точке
в точке 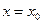 слева, а если
слева, а если 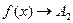 при
при 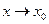 только при
только при 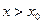 , то
, то  называется пределом функции
называется пределом функции  в точке
в точке 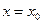 справа.
справа.
Пределы функции слева или только справа называются односторонними пределами(рис. 4).

Рисунок 4.
Если существуют оба односторонних предела и они равны, то существует предел  :
:
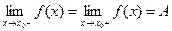
Бесконечно малые и бесконечно большие функции
Функция  называется бесконечно малой при
называется бесконечно малой при 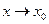 , если
, если 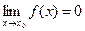
Две бесконечно малые функции f (x) и g (x) при 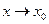 называются эквивалентными бесконечно малыми, если
называются эквивалентными бесконечно малыми, если 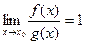 .
.
Таблица 2.
Основные эквивалентности (при 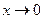 )
)
Функция 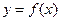 называется бесконечно большой при
называется бесконечно большой при 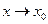 , если
, если 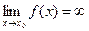
Основные теоремы о конечных пределах.
1. Если  = С (С – константа) при
= С (С – константа) при  , то
, то
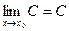 .
.
2. 
3.  , если
, если  – функция, непрерывная в точке
– функция, непрерывная в точке 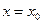 .
.
4. Если  и
и 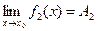 , то
, то
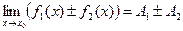
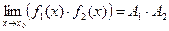
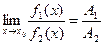
Раскрытие неопределенностей
Чтобы вычислить предел, имеющий неопределенность, нужно предварительно преобразовать функцию, стоящую под знаком предела так, чтобы неопределенность исчезла, т.е. раскрыть неопределенность. Основные виды неопределенностей:  .
.
|
|
|
Правило 1. Чтобы раскрыть неопределенность  при
при  , образованную
, образованную
отношением двух функций, нужно выражения в числителе и знаменателе почленно поделить на х в старшей степени.
Правило 2. Чтобы раскрыть неопределенность  при
при 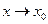 (где
(где  – число), образованную отношением двух функций, нужно в числителе и знаменателе дроби выделить критический множитель (х –
– число), образованную отношением двух функций, нужно в числителе и знаменателе дроби выделить критический множитель (х –  ), и сократить на него дробь.
), и сократить на него дробь.
Для выделения критического множителя в случае, когда данная неопределенность образована отношением тригонометрических, показательных, или логарифмических функций, используют замену бесконечно малых функций на их эквивалентности (см. таблицу 2).
Правило 3. Чтобы раскрыть неопределенность 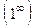 , нужно свести ее ко второму замечательному пределу:
, нужно свести ее ко второму замечательному пределу:
 или
или  .
.
|
|
|