Расчёт надёжности при основном соединении элементов в электрических аппаратах

Основным (последовательным) соединением элементов в сис­теме называется такое соединение, при котором отказ ЭА насту­пает в случае отказа любого из элементов (рис. 6.4).

Рис. 6.4

Основные соединения элементов ЭА

 

В этом случае вероятность безотказной работы ЭА, состоящей из N элементов, при условии, что отказы элементов независимы:

(6.1)

где P(t) — вероятность безотказной работы i-го элемента.

ВБР P(t) можно выразить через интенсивность отказов элемен­тов:

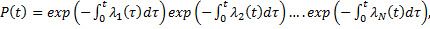(6.2)

где λ_i(t) — интенсивность отказов ί-го элемента системы, i = 1,..., N.

При расчете надежности ЭА с основным соединением элемен­тов и учетом лишь внезапных отказов обычно принимают допу­щение о простейшем характере потока отказов.

Так как поток отказов считается стационарным, то

(6.3)

Вычисление других количественных характеристик безотказ­ности ЭА в этом случае производится по следующим формулам:

§ интенсивность отказов

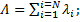(6.4)

§ средняя наработка до отказа

(6.5)

§ плотность распределения времени безотказной работы

(6.6)

Данный метод расчета надежности ЭА является наиболее про­стым, но имеет недостатки. Во-первых, элементы в ЭА работают в различных условиях по коэффициенту нагрузки, температуре, давлению и влажности окружающей среды, вибрации, радиаци­онному облучению и т. п. Поэтому при расчете надежности по это­му методу необходимо знать характеристики элементов в зависи­мости от условий эксплуатации. П ока для большинства элементов сложных ЭА зависимости λ = f (t, x), где — вектор эксплуатаци­онных факторов, не получены. Во-вторых, на ранних стадиях про­ектирования систем (т. е. при ориентировочном расчете надежно­сти) трудно установить режимы работы элементов. Вот почему рассматриваемый метод целесообразно применять при оконча­тельном расчете надежности системы, когда построены опытные образцы объекта и экспериментально определены режимы рабо­ты элемента.

Продолжительность работы по времени t ЭА можно разбить на три участка: приработки узлов аппарата; нормальной работы; ста­рения.

Вероятность безотказной работы аппарата представится в виде

где P ₁(t) — вероятность безотказной работы на первом участке; P₂(t) — на втором; P₃(t) — на третьем при учете износа дугогаси­тельного устройства и износа главных дугогасительных контактов.

Стендовые испытания показывают [20], что вероятность отка­зов на первом участке находится в пределах от 0,001 до 0,006. Сле­довательно, P₁ = 0,999...0,994.

Вероятность безотказной работы на втором участке соответст­вует экспоненциальному закону:

P₂ (t) = exp (-λt).

На третьем участке имеют место два состояния: безотказной работы р и отказа (1 - p). Аппарат в каждый конкретный момент может находиться в состоянии безотказной работы (их число — n). Полная вероятность безотказной работы на третьем участке будет подчиняться биномиальному закону распределения:

При ориентировочном расчете, позволяющем в начале проек­тирования объекта оценить надежность различных схемных ва­риантов и вовремя внести изменения в структурную схему, повы­сив тем самым надежность, принимают следующие допущения:

§ интенсивности отказов элементов известны;

§ известно число элементов каждого типа;

§ однотипные элементы равнонадежны, т. е. имеют одинаковую интенсивность отказов, равную ее среднестатистическому зна­чению;

§ все элементы работают в номинальном режиме.

Тогда

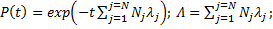
(6.7)

где λj — среднестатистическая интенсивность отказов j- го элемен­та; Nj — число элементов j -го типа; m — число типов элементов.

Таким образом, для ориентировочного расчета надежности ЭА любой степени сложности достаточно знать состав элементов, их число и среднестатистическое значение интенсивности отказов элементов каждого типа. Состав элементов и их количество берут­ся из структурной схемы ЭА. Среднестатистические данные о λ -характеристиках получают по данным специальных испытаний на надежность либо на основании анализа процесса эксплуатации

 

 

 

 

ЭА, подобных проектируемым. Например, интенсивность отказов на первом участке можно снизить, контролируя изготовление де­талей и сборку ЭА. Третий участок отказов можно уменьшить, используя материалы, которые практически не стареют, а также вовремя проводя профилактику ЭА. Продолжительность второго участка зависит от режима эксплуатации.

Математическое описание процесса возникновения отказа на­зывается моделью отказов.

Так как 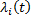одних и тех же элементов, работающих в различ­ных ЭА, могут отличаться, то целесообразно вести расчет надеж­ности проектируемого ЭА для двух крайних значений интенсив­ностей отказов λ_min и λ_max. Тем самым устанавливаются границы, внутри которых будут находиться количественные характеристи­ки надежности (рис. 6.5).

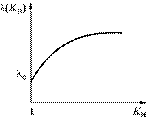
Для учета режима работы элементов при расчете надежности используется понятие коэффициента нагрузки К_н — отношение рабочего значения нагрузки к ее номинальному значению. (Номи­нальная температура при тепловой нагрузке принимается 25°С, при вибрационной g = 9,82м/с² ит. д.) При К_н = 1 интенсивность отказов λ = λ₀. Функция λ = λ(К_н) является монотонно возрастаю­щей (рис. 6.6).

Если необходимо учитывать несколько видов нагрузки, то при­нимается во внимание независимость воздействия нагрузок:

(6.8)

где s — число учитываемых видов нагрузки; h — поправочный коэффициент нагрузки.

При циклическом характере эксплуатации ЭА происходит увеличение интенсивности отказов из-за увеличения нагрузок в моменты включения (выключения) или не стационарности тепловых процессов:

где 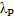— интенсивность отказов при непрерывной работе объекта; — интенсивность отказов на один цикл включения; I — сред­няя частота включений.

Общее время эксплуатации периодически работающего ЭА мо­жет быть разделено на два промежутка: t_Р — нахождение объекта в рабочем состоянии, t_XP — в выключенном состоянии. Для этих промежутков времени интенсивности отказов, соответственно, рав­ны λ_P и λ_ХР. При экспоненциальном законе надежности учет рабо­ты, хранения и включения ЭА можно производить по формуле

(6.9)

где

N_ц — общее число циклов включений ЭА.

При проектировании новых видов ЭА могут отсутствовать дан­ные по интенсивности отказов некоторых элементов. В этом слу­чае может быть использован коэффициентный метод расчета на­дежности. Допущения, принимаемые при этом методе расчета на­дежности, следующие:

§ поток отказов — простейший;

§ интенсивности отказов всех элементов ЭА изменяются в зави­симости от условий эксплуатации в одинаковой мере.

Первое условие означает, что справедлив экспоненциальный

закон надежности, а второе — что при различных условиях экс­плуатации имеет место соотношение

(6.10)

где λ₀ — интенсивность отказов элемента ЭА, количественные ха­рактеристики надежности которого достоверно известны.

Тот элемент, который имеет интенсивность отказов λ₀, есть ос­новной элемент расчета надежности ЭА, a Kj — коэффициент на­дежности j- го элемента. В качестве основных элементов расчета надежности ЭА используются такие элементы, как контакты, ре­зисторы, полупроводниковые приборы и т. д. Коэффициенты на­дежности элементов приводятся в справочниках по надежности.

Соотношение для расчета характеристик надежности имеют вид

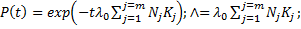(6.11)

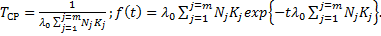
Порядок расчета надежности. Методика оценки безотказно­сти ЭА состоит в выполнении следующих этапов:

1) Формулировка понятия отказа ЭА.

2) Составление схемы расчета надежности, в которой указыва­ется время работы каждого блока.

3) Выбор метода расчета надежности.

4) Составление таблицы расчета надежности.

5) Расчет характеристик надежности.

6) Выводы и рекомендации, направленные на повышение на­дежности ЭА.

При расчете надежности ЭА часто приходится перемножать ве­роятности безотказной работы отдельных элементов расчета, воз­водить их в степень и извлекать корни. При значениях P (t), близ­ких к единице, эти вычисления можно с достаточной для практики точностью выполнять по следующим формулам (для N однотипных элементов):

(6.12)

Таблица 6.1 - Расчет надежности

Тип элемента	Коэффициент нагрузки		Наименование элементов счета
Блок№1	Блок № 2	…	Блок № 3 k

 

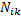
6.4

⇐ Предыдущая19202122232425262728Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: