Наиболее распространенные логические операции для двух простых высказываний

 

 

Название операции	Результат a/b функции а/6	Обозначе­ние опера­ции
0/0	0/1	1/0	1/1
Конъюнкция (логическое умножение)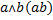
Дизъюнкция (логическое суммирование)
Суммирование по модулю 2
Эквивалентность
Отрицание
Импликация от b к а
Отрицание конъюнкции (штрих Шеффера)
Отрицание дизъюнкции (стрелка Пирса)

Правила перехода от любого сложного высказывания к выска­зыванию, содержащему операции конъюнкции, дизъюнкции и отрицания:

1) из таблицы выделить наборы простых высказываний, при­водящие сложное высказывание в единицу;

2) для каждого из таких наборов записать простые истинные высказывания без знака отрицания, а ложные — со знаком отри­цания; полученные высказывания соединить знаком конъюнкции;

3) конъюнкции простых высказываний соединить операцией дизъюнкции.

Основные логические связки рассмотрены в главе 3 данного пособия. Здесь приведены логические операции, используемые при расчетах надежности резервированных ЭА.

При расчетах надежности наиболее часто используются зако­ны и правила для преобразований сложных высказываний. С их помощью сложную логическую функцию можно привести к ми­нимальной бесповторной форме, т. е. к виду, когда функция со­держит минимальное число составляющих и в ней нет повторения одинаковых аргументов.

1.

2.

3.

4.

5.

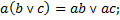
6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

Логическое уравнение, содержащее операции дизъюнкции, конъюнкции и отрицания, можно привести к арифметическому виду, если заменить логические операции на арифметические по следующему правилу: для определения вероятностей сложных высказываний необходимо логическую операцию сложного выска­зывания привести к минимальной бесповторной форме, арифметизировать ее и затем заменить высказывания на их вероятности:

(7.23)

Рис. 7.10 Структура расчета надежности

Расчет надежности, основанный на использовании параллель­но-последовательных структур. Параллельно-последовательная структура надежности объекта дает представление о связи между надежностью объекта и его элементов. Расчет надежности ведется последовательно, начиная от рас­чета элементарных узлов структу­ры к ее все более сложным узлам, и сводится к расчету отдельных участков схемы, состоящих из па­раллельно и последовательно со­единенных элементов. Например, на рис. 7.10 узел, состоящий из элементов 1—2 — элементарный, узел 1-2-3-4 — сложный.

Эта структура может быть сведена к эквивалентной, состоя­щей из узла 1-2-3-4 и элемента 5, соединенных последовательно.

Расчетные формулы для элементов, соединенных парал­лельно. Рассмотрим параллельное соединение из трех элемен­тов (см. рис. 7.11). Его отказ произойдет после выхода из строя всех элементов. Условие работоспособности: устройство работоспо­собно, если работоспособны элемент а, или элемент b, или элемент с,

или элементы а и b, а и с, b и с, а и b и с. Это­му условию соответствует логическая функ­ция (функция алгебры логики — ФАЛ), в ко­торой а, b, с — события, состоящие в том, что элементы а, b, с находятся в работоспо­собном состоянии:

(7.24)

ФАЛ, связывающую состояния элемента с состоянием системы, называют функцией работоспособности системы Для оценки работоспособных состояний системы используются два понятия:

1) кратчайший путь успешного функционирования, который представляет собой такую конъюнкцию элементов, ни один из ком­понентов которой нельзя изъять, не нарушив условия функцио­нирования системы;

2) минимальное сечение отказов — конъюнкция из отрицаний элементов, ни один из компонентов которой нельзя изъять, не на­рушив условия неработоспособности системы.

Используя эти понятия, условия работоспособности объекта можно записать либо в виде дизъюнкции всех кратчайших путей успешного функционирования — дизъюнктивная нормальная фор­ма (ДНФ), либо в виде конъюнкции отрицаний всех минимальных сечений отказов — конъюнктивная нормальная форма (КНФ). Далее, после составления функции работоспособности системы в виде ДНФ или КНФ необходимо перейти к вероятностной функ­ции, с помощью которой определяются характеристики надежно­сти. Однако непосредственно перейти к вероятностной функции от ДНФ или КНФ, как правило, нельзя, так как одна и та же пере­менная может входить в состав нескольких конъюнкций (7.24). Поэтому полученное выражение (7.24) необходимо преобразовать к бесповторной форме функции алгебры логики (БФАЛ). Имеется несколько алгоритмов преобразования ФАЛ и БФАЛ: алгоритмы С. В. Макарова, Ю. Б. Мерекина, И. А. Рябинина, А. С. Смирнова и др.

Минимизируем выражение (7.24):

Fn = а (1 v b v bc)v b (1v с v ас)v c (l v a v ab)= a v b vc, (7.25)

и арифметизируем его:

F_a = a + b + с - (ab + ас + bc) + abc. (7.26)

Теперь заменим события их вероятностями и получим

(7.27)

ВБР системы, состоящей из N параллельно соединенных эле­ментов:

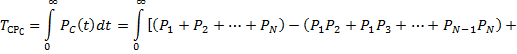
(7.28)

Интенсивность отказов объекта, состоящего из N параллельно соединенных элементов, обладающих постоянной интенсивностью отказов λ_о:

(7.29)

Расчетные формулы для объекта, состоящего из последова­тельно соединенных элементов. Пусть система для простоты со­стоит из трех последовательно соединенных элементов а, b, с. От­каз системы произойдет при отказе любого из элементов. Условие работоспособности: система работоспособна, если работоспособны элемент а и элемент b, и элемент с. Этому условию соответствует логическая функция

(7.30)

Ее арифметическое представление совпадает с логическим:

Вероятность безотказной работы

(7.31)

Для системы, состоящей из N последовательно соединенных элементов,

Последовательность логико-вероятностных расчетов надежно­сти резервированных объектов. Относительная простота расчетов надежности, основанных на использовании параллельно-последо­вательных структур, делает их самыми распространенными в ин­женерной практике. Однако не всегда условие работоспособности можно непосредственно представить параллельно-последователь­ной структурой. В этом случае сложную структуру можно заме­нить ее эквивалентной параллельно-последовательной структурой. К таким преобразованиям относятся:

а) преобразование с эквивалентной заменой треугольника на звезду и обратно;

б) разложение сложной структуры по базовому элементу.
Способы преобразования сложных структур изложены в кни­ге И. А. Рябинина [14].

Последовательность логико-вероятностного метода расчета надежности объектов следующая:

1. Словесная формулировка условий работоспособности системы.

2. Составление логической функции работоспособности.

3. Минимизация и приведение к бесповторной форме.

4. Арифметизация .

5. Замена событий (высказываний) их вероятностями.

6. Расчет надежности (определение P_c (t), fc (t), A_c (t)и других характеристик).

7. Анализ полученных результатов.

 

7.5.

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: