Модели случайных процессов

В ТЕОРИИ НАДЕЖНОСТИ

Случайной функцией (или случайным анализом) на вероятно­стном пространстве называется семейство случайных ве­личин зависящих от вещественного параметра t, принимаю­щего значения из некоторого множества Т. Это множество назы­вается областью определения функции. Пространство X, в котором принимает свои значения, называется фазовым пространст­вом функции. При обозначении случайных величин аргумент ω часто опускают и пишут ξ(t) вместо Параметр t иногда за­писывают в виде индекса

Если Т — подмножество действительной прямой, а параметр t интерпретируется как время , то вместо термина «слу­чайная функция» употребляется термин «случайный процесс». Если Т состоит из целых чисел, то говорят также о случайной по­следовательности.

Здесь рассматриваются в основном случайные процессы. Если в функции зафиксировать элементарное событие ω, то это уже не случайная функция от , а выборочная (ее еще называ­ют траекторией или путями случайного процесса). Однако в каждой точке являются случайными величинами.

Одной из основных характеристик случайного процесса явля­ются его конечномерные (частные) распределения — набор функ­ций, определенных для каждого натурального k соотношениями

(5.6)

где множества из области значений процесса.

Явные выражения для конечномерных функций распределе­ния случайного процесса часто бывают сложными и неудобными в инженерных применениях. Поэтому в ряде случаев задают конеч­номерные распределения их плотностями или характеристически­
ми функциями. Если плотность распреде­ления функции распределения , то

(5.7)

Характеристическая функция конечномерного распределения определяется формулой

(5.8)

где — вещественные числа.

Характеристическая функция является преобразованием Фу­рье плотности распределения

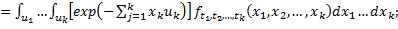(5.9)

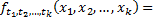
(5.10)

Два случайных процесса называются стохастически эквива­лентными в широком смысле, если совпадают их конечномерные распределения.

В теории случайных процессов выделяются в зависимости от при­меняемых методов и объектов исследования различные классы.

1. Случайный процесс называется гауссовским, если все его конечномерные распределения — гауссовские, т. е. случай­ный вектор имеет нормальное распределение при любых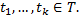

2. Случайный процесс называется процессом с неза­висимыми приращениями, если его приращения на непересекаю­щихся отрезках не зависят друг от друга: для

случайные величины независимы.

3. Случайный процесс называется процессом с некоррелированными приращениями, если его приращения на не­пересекающихся отрезках некоррелированы, т. е. для имеем

Если — процесс с независимыми приращениями, , то он также является и процессом с некоррелированными прира­щениями; если — гауссовский процесс с некоррелированны­ми приращениями, то это также и процесс с независимыми прира­щениями.

4. Случайный процесс называется стационарным, если для любого действительного h его конечномерные распреде­ления не меняются при сдвиге на h:

(5.11)

если только

5. Марковские случайные процессы — это процессы, в кото­рых будущее и прошлое при фиксированном настоящем независи­мы, или те, в которых будущее зависит от прошлого только через настоящее.

Важный класс случайных процессов образуют стационарные процессы, те или иные характеристики которых остаются неиз­менными от начала интервала и во всем интервале. В более общем случае стационарными называют такие случайные процессы, оп­ределенные характеристики которых инвариантны относительно некоторой группы или полугруппы преобразований. В качестве характеристик случайных процессов чаще всего выступают конеч­номерные распределения.

Однако еще важнее процессы, обладающие свойством стацио­нарности второго порядка, обычно называемые стационарными в широком смысле, т. е. зависящие не от начала интервала, но от рас­сматриваемого интервала. Если в качестве инвариантных характе­ристик выбираются конечномерные распределения, то соответст­вующие процессы называют стационарными в узком смысле.

Спектральное представление случайных процессов. Техноло­гические и режимные параметры объектов часто представляют собой колебания со случайными составляющими, являясь стацио­нарными в широком смысле случайными процессами. В этом пла­не для физической интерпретации таких случайных процессов вводятся следующие термины.

Энергией, переносимой случайным процессом ξ(t) в течение промежутка времени называется величина

Полной энергией, переносимой процессом на­зывается интеграл

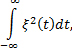
если он существует.

Средней мощностью случайного процесса называется предел

Если процесс ξ(t) является комплексным, то вместо в пре­дыдущих выражениях следует писать

Случайные процессы удобно моделировать суммами гармоник, с заданными частотами и случайными амплитудами A (t)и фаза­ми φ(t):

Теоретико-вероятностная структура этого процесса полностью определяется совместным распределением случайных величин , Во многих случаях целесообразно рассматри­вать комплекснозначные случайные процессы колебательного ха­рактера

(5.12)

где комплексные амплитуды - являются случайными величина­ми вещественны. При этом совокупность всех частот рассматриваемая как множество точек на прямой 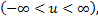называется спектром случайного процесса. Случайный процесс ξ(t)можно расщепить на вещественную и мнимую части:

где

Средняя мощность, переносимая случайным колебательным процессом ξ(t):

Каноническое представление случайных процессов. В ряде случаев для описания случайного процесса применяют представление его через сумму случайных процессов более простого вида.
Один из способов такого представления называется каноническим разложением:

(5.13)

где координатные функции, являющиеся неслу­чайными функциями времени; 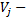коэффициенты, являющиеся некоррелированными случайными величинами с нулевыми мате­матическими ожиданиями и дисперсиями

В качестве координатных функций в канонических разложе­ниях используют семейства функций, обладающих свойством ортонормированности:

Квазистационарные случайные процессы. Технологические процессы, протекающие в сложных системах, под влиянием раз­нообразных факторов конструктивного, производственного и экс­плуатационного характера изменяются случайным и неслучайным образом во времени. Поэтому при математическом описании тех­нологических процессов необходимо учитывать нестационарность случайных процессов. Вид нестационарности случайных процес­сов в оборудовании может быть различным.

1. Случайный процесс ξ(t) называется нестационарным по ма­тематическому ожиданию, если он имеет вид

(5.14)

где a (t)— неслучайная функция времени; 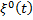— стационарный случайный процесс.

2. Случайный процесс ξ(t) называется нестационарным по дис­персии, если он представим в виде произведения

(5.15)

где — функция изменения дисперсии во времени.

3. Случайный процесс ξ(t) может быть нестационарным и по математическому ожиданию, и по дисперсии одновременно:

(5.16)

при этом считается, что

Решение многих статистических задач для квазистационар­ных процессов часто сводится к стационарному случаю.

⇐ Предыдущая15161718192021222324Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: