Расчет надежности при общем и раздельном резервировании

Общее резервирование с постоянно включенным резервом (см. рис. 7.3). Допущения:

1) отказы элементов системы описываются простейшим пото­ком отказов;

2) резервируемые и резервные элементы равнонадежны.

Задано:

1) число основных элементов в объекте N;

2) ВБР i- гоэлемента;

3) кратность резервирования.

Требуется определить характеристики надежности резервиро­ванной системы.

ВБР системы без резервирования при независимых отказах

(7.1)

вероятность отказа

(7.2)

Вероятность отказа объекта с общим резервированием составит

(7.3)

В случае равенства вероятностей отказа основного и резервно­го объектов

(7.4)

или

(7.5)

 

 

Для экспоненциального закона надежности

где

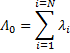
— интенсивность отказов любого из m+1 объектов;

(7.6)

плотность вероятности

(7.7)

интенсивность отказов

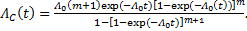(7.8)

При анализе надежности резервированных устройств на этапе проектирования приходится сравнивать различные схемные ре­шения. В этом случае за критерий качества резервирования при­нимается выигрыш надежности — отношение количественной характеристики надежности резервированного устройства к той же количественной характеристике нерезервированного устрой­ства или устройства с другим видом резервирования. Наиболее часто используются следующие критерии качества резервированных устройств:

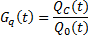
— выигрыш надежности в течение времени t по вероятности отказов;

— выигрыш надежности в течение времени t по вероятности без­отказной работы;

— выигрыш надежности по среднему времени безотказной работы.

Выигрыш надежности резервированной системы существенно зависит от того, какой количественной характеристикой оцени­вается надежность, т. е.

(7.9)

Общее резервирование с замещением (см. рис. 7.5). Выраже­ния (7.1)...(7.9) пригодны для расчета надежности резервирован­ных систем при наличии идеального (абсолютно надежного) пере­ключателя. На самом деле переключатель имеет отказы различ­ного характера: несрабатывание, ложное срабатывание, отказы, которые выводят из строя резервную группу в целом. Поэтому при наличии переключателя

(7.10)

Раздельное резервирование с постоянно включенным резер­вом (см. рис. 7.4). Вероятность того, что произойдет отказ систе­мы из-за отказов элементов i -го типа, равна произведению вероят­ностей отказов i -го элемента и всех его резервирующих, т. е.

(7.11)

а ВБР

(7.12)

Так как обычно основные и резервные элементы равнонадёжны, то

(7.13)

Функциональные группы соединены в системе последователь­но, отказы их принимаем независимыми, поэтому

(7.14)

Вычисление по P_c(t)других количественных характеристик на­дежности резервированных систем, содержащих большое число эле­ментов, затруднительно. Поэтому примем упрощающие допущения. Предположим, что все элементы системы равнонадежны, тогда

(7.15)

где интенсивность отказов λ представляет собойсредневзвешен­ное значение интенсивностей отказов всех элементов, из которых состоит объект:

или

(7.16)

Выражение для вычисления впредположе­нии о равнонадежности элементов объекта имеют вид

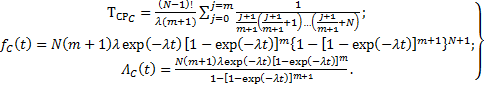(7.17)

7.3.

РАСЧЕТ НАДЕЖНОСТИ ПРИ РЕЗЕРВИРОВАНИИ ОБЪЕКТОВ

С ДРОБНОЙ КРАТНОСТЬЮ

Рассмотрим случай резервирования объекта с дробной кратно­стью и нагруженным резервом (рис. 7.9).

При таком резервировании нормальная работа резервирован­ного соединения возможна при условии, если число исправных элементов не меньше необходимого для нормальной работы.

Кратность резервирования определяется из соотношения

(7.18)

Рис. 7.9 Резервирование с дробной кратно­стью при нагруженном резерве

где Z — общее число элементов расчета резервированного сое­динения; N — число элементов, необходимое длянормальной работы соединения; Z - N — число резервных элементов.

В случае общего резервирования (см. рис. 7.3, 7.5) кратность резервирования всегда равна числу резервных устройств.

В общем случае т является числом дробным. Однако может оказаться, что при делении величины Z — N на ЛГ кратность резер­вирования т получается числом целым. Так как одно и то же т может получаться при различных Z и N, то кратность резервиро­вания следует записывать в виде простой дроби без сокращения. Например, если записано т = 4/2, то это означает, что здесь имеет место резервирование с дробной кратностью, причем для нормаль­ной работы объекта необходимо не менее 2 элементов, а число ре­зервных элементов равно 4. Записать в данном случае т = 2 нель­зя — такая запись означает, что имеет место резервирование с це­лой кратностью, причем число резервных элементов равно 2, общее число элементов — 3.

Пусть резервированная система состоит из N основных и К ре­зервных элементов

(N > К). При отказе одного из основных эле­ментов на его место без перерыва в работе включается один из ре­зервных (резервные элементы также могут отказывать). Таких замещений, не нарушающих работу резервированной системы в целом, не может быть больше К.

Средняя наработка до отказа рассматриваемой резервирован­ной системы в предположении абсолютно надежных переключаю­щих устройств и равнонадежных элементов, с интенсивностью отказов каждого λ, составит

(7.19)

Найдем вероятность безотказной работы объекта. Безотказная работа объекта в течение времени t будет иметь место, если за это время осуществится хотя бы одна из гипотез:

Н_о — все элементы исправны;

Н₁ — один элемент отказал, (К + N - 1) элементов исправны;

(H_i - i)элементов отказали, (К + N - i)элементов исправны;

(Н_к - К)элементов отказали, N элементов исправны.

Число различных вариантов

(7.20)

Тогда ВБР системы можно определить из выражения

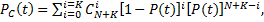(7.21)

где P (t)— ВБР элемента при условии, что все элементы равнонадежны.

Для мажоритарного резервирования по схеме «2 из 3» ВБР сис­темы можно подсчитать по формуле

(7.22)

где P (t)— ВБР одного канала (элемента, подсистемы); P _M(t)— ВБР мажоритарного органа.

7.4.

⇐ Предыдущая22232425262728293031Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: