Потоки отказав и восстановлений

В ТЕОРИИ НАДЕЖНОСТИ

5.1 ХАРАКТЕРИСТИКА ПОТОКОВ ОТКАЗОВ И ВОССТАНОВЛЕНИЙ

Какбыло показано на рис. 1.3, процесс функцио­нирования объектов состоит из чередующихся слу­чайных событий: исправная работа, отказ, восстанов­ление работоспособности, исправная работа и т. д. По­этому в теории надежности принято пользоваться понятием потока событий — это такая последова­тельность событий, при которой они происходят одно за другим в случайные моменты времени.

Основными потоками событий, изучаемыми в тео­рии надежности, являются потоки отказов и восста­новлений. По своему характеру они могут быть самы­ми разными. Наибольшее применение в теории надеж­ности получили простейший поток и потоки Эрланга.

Среди самых важных характеристик потоков от­казов и восстановлений являются математическое ожидание числа отказов (восстановлений) Ω(t)на интервале (0, t), интенсивность отказа λ(t)или вос­становления μ(t)и ω(t) — параметр потока отказов. Под интенсивностью потока отказов (восстановле­ний) понимается математическое ожидание числа отказов (восстановлений) в единицу времени, т. е.

Простейшим потоком событий называется поток, удовлетворяющий условиям стационарности, орди­нарности и отсутствия последействия.

Стационарность потока отказов означает, что вероятность по­явления определенного числа отказов за определенный интервал времени длительностью t зависит не от того, где располагается на оси времени t этот интервал, а только от его длительности, т. е, плотность потока появления отказов постоянна во времени. Ина­че говоря, вероятность возникновения фиксированного числа от­казов на заданном интервале времени не зависит от выбора начала отсчета времени. Потоки отказов многих объектов в период нор­мальной эксплуатации близки к стационарному потоку. В перио­ды приработки и старения объектов потоки отказов являются не­стационарными.

Поток отказов принадлежит к классу ординарных потоков, если вероятность возникновения двух и более отказов за проме­жуток времени At пренебрежимо мала по сравнению с вероятно­стью возникновения одного отказа, т. е.

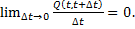(5.1)

Иными словами, ординарность потока исключает случаи од­новременного возникновения нескольких отказов.

Отсутствие последействия означает, что вероятность возник­новения фиксированного числа отказов на интервале времени (t, t + τ) не зависит от того, сколько отказов возникло до момен­та τ. Аналитически условия принадлежности к классу потоков без последействия можно записать в виде

(5.2)

Для потоков с последействием

(5.3)

Условие (5.3) свидетельствует о том, что отказы являются со­бытиями случайными и независимыми.

Несмотря на то что на практике не всегда наблюдается одно­временное выполнение всех трех указанных условий, простейший поток может служить приближенной физической моделью для широкого круга задач, выдвигаемых требованиями эксплуатации объектов. Доказано, что если поток отказов является простейшим, то он описывается распределением Пуассона с постоянным пара­метром распределения λ:

(5.4)

Поэтому простейший поток часто называют пуассоновским.

Потоки отказов элементов сложных систем часто являются нестационарными. Поток, удовлетворяющий одновременно усло­виям ординарности и отсутствия последействия, но нестационар­ный, называется нестационарным потоком Пуассона. Он наблю­дается в процессе приработки системы и в случае, если элементы сложной системы работают неодновременно из-за износа изоля­ции, нарушения правильной работы ручного или дистанционного привода, а также из-за сбоя последовательности замыкания и раз­мыкания при включении и отключении главных и дугогасительных контактов. На отказ ЭА, расположенных на открытой мест­ности, влияют погодные явления.

Нарушение условий стационарности или наличие последствия приводит к тому, что поток становится не простейшим. К не про­стейшим потокам относятся потоки Эрланга, которые возникают вследствие «просеивания» простейшего потока отказов. Потоком Эрланга k -го порядка называется поток, получающийся в резуль­тате сохранения каждого k -го события в простейшем потоке. При k = 1 поток Эрланга — простейший. С увеличением числа k послед­ствие возрастает. При поток приближается к регулярному потоку с постоянным интервалом между событиями

Дифференциальный закон распределения потока Эрланга опи­сывается формулой

(5.5)

где λ— интенсивность простейшего исходного потока.

Интенсивность отказов при потоке Эрланга:

математическое ожидание времени между событиями:

дисперсия времени между событиями:

 

⇐ Предыдущая14151617181920212223Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: