 |
Марковские процессы в теории надежности
|
|
|
|
Марковские процессы играют чрезвычайно важную роль в различных приложениях. Хотя эти процессы представляют собой весьма специальный класс случайных процессов, значение их для теории надежности, особенно для решения задач прогнозирования характеристик надежности, очень велико. При определении характеристик надежности оборудования сложных технологических систем в процессе эксплуатации и прогнозирования остаточного ресурса наибольший интерес представляют процессы Маркова с непрерывным временем, которые и будут здесь рассмотрены.
Марковское свойство. В основе понятия марковского процесса лежит представление об изменяющихся во времени системах, обладающих свойством «отсутствия последействия» («отсутствия памяти»). Пусть имеется некоторое вероятностное пространство {Ω, ψ, P }. Время изменяется на некотором отрезке (интервале, полуинтервале) τ (например, τ = [0, ∞]), содержащемся во множестве всех действительных неотрицательных чисел. Поток σ-алгебр  задан, т. е. задано такое семейство σ-алгебр
задан, т. е. задано такое семейство σ-алгебр 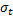 , что
, что  Задана также функция двух переменных
Задана также функция двух переменных 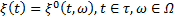 со значениями в некотором измеримом пространстве (X, β) такая, что ξ(t) при каждом
со значениями в некотором измеримом пространстве (X, β) такая, что ξ(t) при каждом  является измеримым отображением пространства
является измеримым отображением пространства 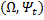 в (X, β). Тем самым задан случайный процесс ξ(t) подчиненный потоку σ-алгебр
в (X, β). Тем самым задан случайный процесс ξ(t) подчиненный потоку σ-алгебр  .
.
Случайный процесс ξ(t), подчиненный потоку σ-алгебр 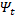 , обладает марковским свойством относительно этого потока, если при всех
, обладает марковским свойством относительно этого потока, если при всех  с вероятностью 1 выполняется соотношение
с вероятностью 1 выполняется соотношение
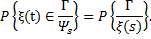
Такой процесс принято называть марковской случайной функцией. Измеримое пространство (X, Ψ)называется фазовым пространством, а точки фазового пространства — состояниями.
|
|
|
Если ξ(t) интерпретировать как состояние некоторой системы в момент времени t, то марковское свойство означает, что такая система обладает свойством отсутствия последействия: при прогнозировании поведения системы в «будущие» моменты времени по наблюдениям за системой во все «прошедшие» моменты времени вплоть до «настоящего» существенным является знание состояния системы лишь в «настоящий» момент времени.
Вероятность перехода. Пусть 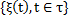 — марковская случайная функция. Следствием марковского свойства и формулы полной вероятности является соотношение
— марковская случайная функция. Следствием марковского свойства и формулы полной вероятности является соотношение
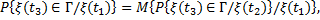 (5.17)
(5.17)
справедливое почти наверное относительно меры Р при всех  и
и 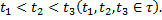 Это соотношение называется уравнением Колмогорова — Чепмена.
Это соотношение называется уравнением Колмогорова — Чепмена.
Особый интерес представляет случай, когда для условной вероятности 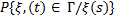 существует условная вероятность, т. е. такая функция
существует условная вероятность, т. е. такая функция 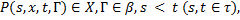 что выполняются условия:
что выполняются условия:
а) при фиксированных s, t, Г функция P (s, x, t, Г) является вероятностной мерой на (X, β);
б) при фиксированных s, t, Г функция P (s, х, t, Г) измерима;
в) с вероятностью 1 при всех s, t, Г
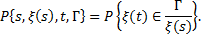
Если для данной марковской случайной функции существует функция P (s, х, t, Г), удовлетворяющая условиям (а...в), то она называется вероятностью перехода (переходной вероятностью). В терминах вероятности перехода уравнение Колмогорова — Чеп-мена запишется в виде
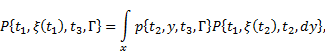
где 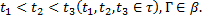
Определение марковского процесса. При изучении марковского свойства удобно не фиксировать начальное распределение процесса (да и сам начальный момент времени), а рассматривать целое семейство марковских случайных функций, «начинающихся» в произвольный момент времени в произвольной точке фазового пространства. Это означает, что на вероятностном пространстве имеется уже не одна фиксированная вероятностная мера, а семейство мер  зависящих от временной и фазовой переменных и связанных между собой марковским свойством. При этом мера
зависящих от временной и фазовой переменных и связанных между собой марковским свойством. При этом мера  интерпретируется как условная вероятность некоторого события, которое может произойти после момента времени s при условии, что ξ(s) = х.
интерпретируется как условная вероятность некоторого события, которое может произойти после момента времени s при условии, что ξ(s) = х.
|
|
|
Если заданы пространство элементарных событий 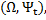 семейство σ-алгебр
семейство σ-алгебр  функция двух переменных
функция двух переменных 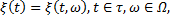 со значениями в измеримом пространстве (X, β) и семейство вероятностных мер
со значениями в измеримом пространстве (X, β) и семейство вероятностных мер  на σ-алгебре
на σ-алгебре 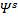 , то система этих объектов называется марковским процессом при выполнении следующих условий:
, то система этих объектов называется марковским процессом при выполнении следующих условий:
1) при любых 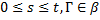 функция
функция 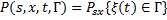 есть β-измеримая функция от х;
есть β-измеримая функция от х;
2) при любых 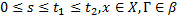 с вероятностью
с вероятностью 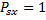 выполнено соотношение
выполнено соотношение

Строгая марковость. Случайную величину υ = υ(ω) со значениями в (s, ∞) будем называть марковским моментом относительно потока σ-алгебр 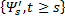 , если при всех
, если при всех  выполняется условие
выполняется условие 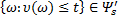 . Марковские моменты называют иногда величинами, не зависящими от будущего, так как наглядно условие
. Марковские моменты называют иногда величинами, не зависящими от будущего, так как наглядно условие 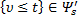 означает, что наступление или ненаступление события
означает, что наступление или ненаступление события  зависит лишь от явлений, наблюдаемых в течение времени от момента s до момента t.
зависит лишь от явлений, наблюдаемых в течение времени от момента s до момента t.
Марковский процесс ξ(t)в фазовом пространстве (X, β) называется строго марковским, если выполнены следующие условия:
1) при фиксированном  вероятность перехода P(s, x, t, Г) процесса
вероятность перехода P(s, x, t, Г) процесса 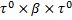 -соизмеримой функции от (s, x, t)на множестве
-соизмеримой функции от (s, x, t)на множестве  здесь
здесь  σ-алгебра борелевских подмножеств полуоси [0, ∞];
σ-алгебра борелевских подмножеств полуоси [0, ∞];
2) для любых  и произвольного марковского момента и относительно потока σ-алгебр выполнено соотношение
и произвольного марковского момента и относительно потока σ-алгебр выполнено соотношение
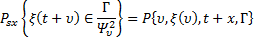
на множестве 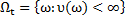 относительно меры
относительно меры 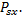
Другими словами, марковский процесс ξ = ξ(t)называется строго марковским, если для любого марковского момента времени и при условии ξ(υ) = х, где х — известное состояние, поведение процесса при t > υ не зависит от его поведения до момента υ, причем переход из х = ξ(υ) в то или иное состояние у через время h осуществляется с такими же вероятностями, как и в случае фиксированного момента υ = s. Точнее, условная вероятность оказаться через время h в множестве Г равна
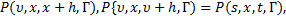
где P (s, х, t, Г) — вероятность перехода марковского процесса.
Если ξ(t) есть случайный вектор в n -мерном пространстве  и его распределение вероятностей при условии ξ(s)= x имеет плотность
и его распределение вероятностей при условии ξ(s)= x имеет плотность  , то
, то
 (5.18)
(5.18)
Условную плотность вероятности  обычно называют переходной плотностью марковского процесса ξ(t).
обычно называют переходной плотностью марковского процесса ξ(t).
Однородные марковские процессы. Марковский процесс ξ(t) называется однородным, если вероятность перехода P (s, x, t, Г) обладает тем свойством, что функция P (s, x, s + h, Г) не зависит от s. Если положить Р (h, х, Г) = P (s, x, s + h, Г), то для конечномерных распределений процесса будет иметь место равенство
|
|
|
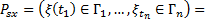
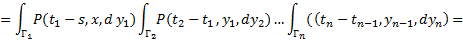
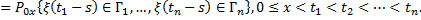
Таким образом, вместо семейства мер  зависящих от временной и пространственной переменных, в однородном случае достаточно семейства мер
зависящих от временной и пространственной переменных, в однородном случае достаточно семейства мер  зависящих лишь от пространственной переменной. Другими словами, каждый раз, когда процесс выходит из состояния х в момент времени s, мы производим сдвиг времени так, чтобы точка s стала начальной (нулевой). Естественно, что при этом необходимо сдвигать и все траектории процесса. Так как закономерности поведения однородного марковского процесса на любом интервале времени (s, t)при известном состоянии ξ(s)= х не зависят от расположения интервала (s, t)на временной оси, то для переходных вероятностей P(s, х, t, Г) это означает фактическую зависимость лишь от разности t — s, а не от t и s, как в общем случае P (s, x, t, Г) = P (t - s, x, Г).
зависящих лишь от пространственной переменной. Другими словами, каждый раз, когда процесс выходит из состояния х в момент времени s, мы производим сдвиг времени так, чтобы точка s стала начальной (нулевой). Естественно, что при этом необходимо сдвигать и все траектории процесса. Так как закономерности поведения однородного марковского процесса на любом интервале времени (s, t)при известном состоянии ξ(s)= х не зависят от расположения интервала (s, t)на временной оси, то для переходных вероятностей P(s, х, t, Г) это означает фактическую зависимость лишь от разности t — s, а не от t и s, как в общем случае P (s, x, t, Г) = P (t - s, x, Г).
Для однородного марковского процесса должны выполняться следующие условия:
1) при любых 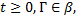 функция
функция  измерима как функция от х, причем
измерима как функция от х, причем 
2) для любых 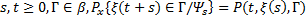 относительно меры
относительно меры 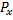 на множестве
на множестве 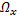 ;
;
3) для каждого 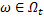 найдется такое
найдется такое 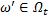 , что
, что 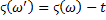 и
и 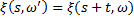 при
при 
Условие 2 соединяет свойство марковости процесса и свойство его однородности во времени. Условие 3 означает, что вместе с каждой траекторией процесса произвольный кусок ее после некоторого момента времени также является возможной траекторией.
Функция P (t, х, Г) — вероятность перехода однородного марковского процесса - удовлетворяет уравнению Колмогорова — Чепмена:
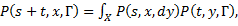 (5.19)
(5.19)
где  При этом
При этом 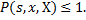
Если 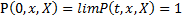 при
при 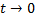 , то вероятность перехода называется нормальной, а соответствующий процесс — нормальным.
, то вероятность перехода называется нормальной, а соответствующий процесс — нормальным.
Инфинитезимальный оператор марковского процесса. Для изучения марковских процессов эффективным средством является теория полугрупп. Пусть ξ(t)— однородный марковский процесс в фазовом пространстве (X, β) с вероятностью перехода P (t, x, Г). Обозначим через В (Х)банахово пространство во всех вещественных ограниченных β-измеримых функциях на X с нормой 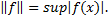 Рассмотрим на В (Х)семейство операторов
Рассмотрим на В (Х)семейство операторов 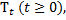 определяемых формулой
определяемых формулой
|
|
|

Из свойств вероятности перехода следуют свойства семейства операторов 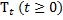 :
:
1) при каждом 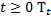 является линейным ограниченным оператором, отображающим В (Х)в В (Х), причем
является линейным ограниченным оператором, отображающим В (Х)в В (Х), причем 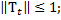
2) при всех 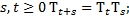
3) если  при всех
при всех 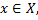 то
то 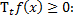 при всех
при всех 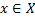 и
и 
4) если 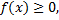 то
то 
5) если при всех 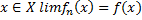 при
при  , где
, где 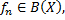 причем
причем 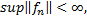 то
то 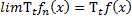 при
при 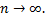
Семейство операторов 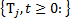 , удовлетворяющих условиям 1 и 2, называется сжимающей полугруппой операторов. А всякий однородный марковский процесс в фазовом пространстве (X, β) порождает сжимающую полугруппу операторов
, удовлетворяющих условиям 1 и 2, называется сжимающей полугруппой операторов. А всякий однородный марковский процесс в фазовом пространстве (X, β) порождает сжимающую полугруппу операторов 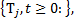 удовлетворяющую условиям 3...5. В свою очередь, всякая сжимающая полугруппа операторов, действующих в В (Х)и удовлетворяющих условиям 3...5, порождает однородную вероятность перехода, причем
удовлетворяющую условиям 3...5. В свою очередь, всякая сжимающая полугруппа операторов, действующих в В (Х)и удовлетворяющих условиям 3...5, порождает однородную вероятность перехода, причем 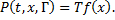
Оператор А полугруппы 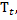 определяемый формулой
определяемый формулой
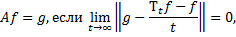
называется инфинитезимальным оператором марковского процесса. Область определения оператора DA состоит из всех тех функций  для которых предел
для которых предел
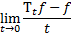
существует равномерно относительно 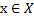 . Очевидно, что
. Очевидно, что
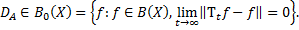
Свойства инфинитезимального оператора:
1) замыкание множества 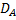 (в смысле сходимости по норме) совпадает с
(в смысле сходимости по норме) совпадает с 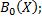
2) если 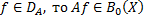 и
и
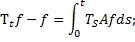
3) если  то функция
то функция  дифференцируема по t (t > 0) и
дифференцируема по t (t > 0) и
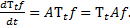 (5.20)
(5.20)
Уравнение (5.20) называется уравнением эволюции;
4) оператор A замкнут.
Инфинитезимальный оператор А является линейным оператором и позволяет перейти от нелинейных уравнений Колмогорова — Чепмена к линейным уравнениям, которые могут быть интегро-дифференциальными уравнениями и уравнениями в частных производных параболического типа.
ВИДЫ МАРКОВСКИХ ПРОЦЕССОВ
При изучении сложных технологических систем, в том числе и ЭА, используют математические модели, основанные на марковских процессах. Основные понятия марковского процесса — состояние и переход системы из одного состояния в другое. Сложные системы в любой момент времени находятся в одном из возможных состояний. Состояние системы часто описывается числом работоспособных элементов. Если рассматривать переходы системы из одного состояния в другое и точно пронумеровать их во времени, поведение системы можно представить как процесс с дискретным временем.
Пусть система находится в одном из 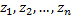 возможных состояний, где номер состояния системы
возможных состояний, где номер состояния системы 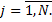 Переход из одного состояния в другое называется шагом процесса. Для описания поведения системы достаточно внести набор условных вероятностей
Переход из одного состояния в другое называется шагом процесса. Для описания поведения системы достаточно внести набор условных вероятностей 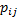 того, что осуществится переход из
того, что осуществится переход из 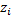 в
в  и задать исходное состояние, в котором находилась система в начальный момент времени. Обозначим через
и задать исходное состояние, в котором находилась система в начальный момент времени. Обозначим через  вероятность того, что система, находясь в момент s в состоянии z, в момент t окажется в одном из состоянии множества Г. Если дополнительные знания о системе в моменты не изменяют этой вероятности при любых s, z, t, Г, то мы имеем дело с марковским процессом.
вероятность того, что система, находясь в момент s в состоянии z, в момент t окажется в одном из состоянии множества Г. Если дополнительные знания о системе в моменты не изменяют этой вероятности при любых s, z, t, Г, то мы имеем дело с марковским процессом.
|
|
|
Обоснование применения марковской модели:
§ если каждый из элементов системы имеет приблизительно экспоненциальное распределение времени безотказной работы;
§ знание какой-либо предыстории системы не представляет большой ценности для предсказания ее поведения в будущем.
Различают следующие основные виды марковских процессов: марковская цепь, марковская последовательность, разрывной марковский процесс, непрерывный марковский процесс, дискретный марковский процесс.
Марковская цепь (дискретный марковский процесс с дискретным временем): в этом случае время t принимает конечное или счетное множество значений 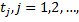 и случайная величина может принимать на этом множестве дискретные значения
и случайная величина может принимать на этом множестве дискретные значения 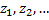 Множества значений {
Множества значений { 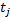 } и {
} и { 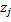 } могут быть конечными или бесконечными.
} могут быть конечными или бесконечными.
Марковская последовательность (непрерывный марковский процесс с дискретным временем) отличается от процесса первого вида тем, что случайная величина 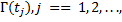 может принимать непрерывное множество значений.
может принимать непрерывное множество значений.
Разрывной марковский процесс (дискретный марковский процесс с непрерывным временем): здесь Г(t) принимает дискретные значения  а время t изменяется непрерывно в интервале [0, Т ], где Т — длина временного интервала, на котором задан процесс Г(t). Множество
а время t изменяется непрерывно в интервале [0, Т ], где Т — длина временного интервала, на котором задан процесс Г(t). Множество 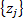 может быть конечным или счетным.
может быть конечным или счетным.
Непрерывный марковский процесс (непрерывный марковский процесс с непрерывным временем): здесь Г(t)принимает значения из некоторого непрерывного множества, параметр t также изменяется непрерывно.
Дискретный марковский процесс (дискретно-непрерывный марковский процесс). В данном случае при непрерывном изменении времени t случайный марковский процесс Г(t) в некоторые моменты времени имеет скачки, а на интервалах времени между скачками ведет себя как непрерывный марковский процесс.
 Помимо перечисленных, возможны более сложные смешанные случайные марковские процессы.
Помимо перечисленных, возможны более сложные смешанные случайные марковские процессы.
При анализе надежности объектов их функционирование обычно рассматривается как случайный процесс перехода объекта из одного состояния в другое, обусловленный отказами и восстановлениями составляющих систему элементов. Этот процесс при определенных условиях может быть достаточно строго описан дискретным марковским
 процессом. Поэтому при анализе надежности объектов наибольшее распространение получили дискретные марковские процессы с непрерывным временем и конечным числом состояний.
процессом. Поэтому при анализе надежности объектов наибольшее распространение получили дискретные марковские процессы с непрерывным временем и конечным числом состояний.
 Отдельную реализацию дискретного марковского процесса можно представить графически в виде ступенчатой функции (рис. 5.1).
Отдельную реализацию дискретного марковского процесса можно представить графически в виде ступенчатой функции (рис. 5.1).
 Процесс Г(t) может принимать только дискретные значения
Процесс Г(t) может принимать только дискретные значения  Смена этих значений - состояний процесса — происходит в некоторые случайные моменты времени
Смена этих значений - состояний процесса — происходит в некоторые случайные моменты времени 
Среди марковских процессов можно выделить так называемые процессы гибели и размножения, т. е. процессы отказа и безотказности.
Рассмотрим функционирование восстанавливаемой системы при следующих предположениях:
1) поток отказов системы носит пуассоновский характер, и интенсивность отказов равна X;
2) время восстановления системы является величиной случайной, распределенной по экспоненциальному закону 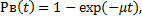 где и — интенсивность восстановления;
где и — интенсивность восстановления;
3) система может находиться в двух состояниях: состоянии 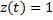 (работоспособности) и состоянии
(работоспособности) и состоянии 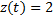 (ремонта).
(ремонта).
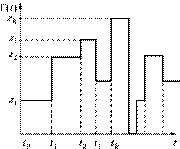
Поведение системы с точки зрения работоспособности опишем графом переходов (рис. 5.2).
На рис. 5.2 кружки с номером означают состояние системы, а стрелки (дуги) — направление переходов системы и вероятности этих переходов за бесконечно малый интервал времени.
Вероятности переходов в силу сделанных предположений и свойства показательного закона надежности не зависят от времени. Введем вероятности нахождения системы в состояниях 1 и 2 как 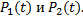 Очевидно, что
Очевидно, что 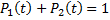 для любого момента времени. Рассмотрим поведение системы в интервале времени [0, t + ∆ t ].Тогда система в момент t + ∆t будет находиться в состоянии 1, если она в момент времени t находилась в этом состоянии и за время ∆t не наблюдалось отказов, а также если система в момент времени t находилась в состоянии 2 и за время ∆t был закончен ее ремонт. Тогда по формуле полной вероятности
для любого момента времени. Рассмотрим поведение системы в интервале времени [0, t + ∆ t ].Тогда система в момент t + ∆t будет находиться в состоянии 1, если она в момент времени t находилась в этом состоянии и за время ∆t не наблюдалось отказов, а также если система в момент времени t находилась в состоянии 2 и за время ∆t был закончен ее ремонт. Тогда по формуле полной вероятности
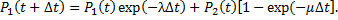
Так как

то

Аналогичные рассуждения приводят к уравнению
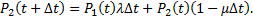
Предельный переход при 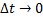 дают дифференциальные уравнения, описывающие поведение системы во времени:
дают дифференциальные уравнения, описывающие поведение системы во времени:
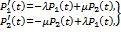 (5.21)
(5.21)
Уравнения вида (5.21) получили название дифференциальных уравнений Колмогорова — Чепмена. Решая их, можно получить
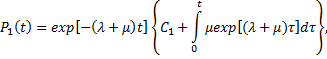
что позволяет оценить вероятности состояния системы в зависимости от начального состояния:
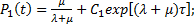 (5.22)
(5.22)

При 
 (5.23)
(5.23)
Для сложной системы, состоящей из разнородных элементов, имеющих различные λ(t)и μ(t), операции составления полного набора радиусов-векторов вершин графа состояний и построение его прямых и обратных ребер могут быть формализованы и производиться на компьютере.
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ
1. Что такое поток событий?
2. Что подразумевается под понятием «простейший поток»?
3. Расскажите о свойствах простейшего потока.
4. Каким условиям удовлетворяет поток Эрланга?
5. Как вы понимаете термины «случайная функция» и «случайный процесс»?
6. Какими характеристиками оценивается случайный процесс?
7. Назовите классы случайных процессов и дайте им краткую характеристику?
8. В чем отличие стационарных случайных процессов в широком и узком смысле?
9. Что такое «эргодическое свойство» стационарного случайного процесса?
10. Расскажите о спектральном представлении случайных процессов.
11. Напишите аналитическое выражение для экспоненциального коррелированного случайного процесса.
12. В чем преимущество канонического представления случайного процесса?
13. Назовите модели нестационарных случайных процессов.
14. Дайте определение марковскому процессу.
15. Как вы понимаете вероятность перехода марковского процесса из одного состояния в другое?
16. Расскажите о инфинитезимальном операторе марковского процесса и его свойствах.
17. Какие вы знаете виды марковских процессов?
18. Какие виды марковских процессов наиболее подходят для описания потоков отказов и восстановлений объектов?
19. Что такое процесс «гибели и размножения»?
20. Сделайте вывод дифференциального уравнения Колмогорова — Чепмена.
21. Оцените вероятность состояния объекта в зависимости от его начального состояния.
РАЗДЕЛ ВТОРОЙ
|
|
|


