 |
И различной глубины контроля
|
|
|
|
Большинство элементов сложных ЭА являются восстанавливаемыми, при этом быстрота и качество восстановления зависят от приспособленности ЭА к ремонту (ремонтопригодности) и от организации восстановления. Применительно к элементам сложных ЭА восстановление включает решение следующих вопросов:
§ обнаружение факта появления отказа;
§ обнаружение места появления отказа;
§ обеспечение хорошей приспособленности к замене отказавших элементов.
В общем случае время после появления отказа может быть разделено на три периода, а именно время с момента:
§ появления отказа до момента установления этого факта системой контроля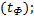 
§ установления факта появления отказа до момента обнаружения места появления отказа 
§ обнаружения места появления отказа до момента замены отказавшего элемента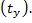 
Длительность каждого из этих периодов зависит от эффективности контроля и поиска места появления отказов, конструкции ЭА, квалификации обслуживающего персонала и т. д. Как правило, основное время затрачивается на поиск отказавшего элемента, поэтому ивремя восстановления будет, в основном, определяться этой величиной.
Выявление мест появления отказа производится с помощью специальных программ, встроенной аппаратуры контроля и контрольно-измерительного оборудования. Сам процесс поиска заключается в последовательной проверке неправильно работающих элементов по определенной программе.
Если законы поиска отказавшего элемента и его замены экспоненциальны
то закон восстановления можно определить следующим образом.
Плотность вероятности двух случайных величин 
и 
составляет
(6.13)
где
При 
получаем уравнение
|
|
|
(6.14)
которое характеризует время восстановления ЭА.
Если известны интенсивности отказов каждого элемента ЭА, то среднее время восстановления при экспоненциальном законе:
(6.15)
где
— интенсивность восстановления i - го элемента; 
среднее время обнаружения места отказа;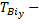 
среднее время устранения отказа.
Определим основные характеристики надежности нерезервированного ЭА, предполагая, что поток отказов простейший и время восстановления экспоненциально. Обратимся к модели системы, изображенной на рис. 5.2 и описываемой выражениями (5.21). Рассмотрим формулу для вероятности нахождения системы в работоспособном состоянии:
(6.16)
Учитывая, что 
Если предположить, что в начальный момент времени ЭА с вероятностью F будет находиться в работоспособном состоянии, т. е. 
тогда
(6.17)
Если перед включением в работу производится проверка объекта, и он оказывается работоспособным, то F = 1 и
(6.18)
Если в момент включения объект неработоспособен (F = 0), то
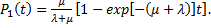(6.19)
Выражения (6.17)...(6.19) характеризуют вероятность работоспособного состояния ЭА в произвольный момент времени t и могут быть использованы для определения функции готовности ЭА.
Введем обозначение 
Тогда выражение (6.19) принимает вид
(6.20)
Для вероятности наступления неработоспособного состояния можно аналогичным путем получить следующую зависимость:
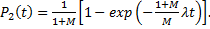(6.21)
При 
, что соответствует условию длительного нахождения ЭА в рабочем состоянии, получим стационарное решение
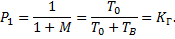
Выражение для определения функции готовности может быть представлено в следующем виде:
Если значение t мало, то
т. е.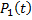 
совпадает с приближенным выражением для ВБР при малых значениях t.
Итак, при малых значениях t функция готовности совпадает с ВБР P (t),при больших — с коэффициентом готовности. Эти выводы получены для простейшего потока отказов и экспоненциальном законе времени восстановления.
|
|
|
Рассмотрим характеристики надежности при произвольных законах отказов и восстановления. Если оценивать произвольный, но достаточно большой промежуток времени t, то, согласно эргодической теореме, вероятности 
и 
можно рассматривать как отрезок времени, в течение которого объект находится в работоспособном или неработоспособном состоянии. Таким образом, величина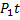 
представляет собой время, в течение которого объект работоспособен, a 
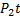— время, затрачиваемое на восстановление работоспособности. Если за время t было п отказов, то средняя наработка на отказ и среднее время восстановления будут соответственно равны
откуда
Так как 
то
Полученные зависимости для оценки надежности нерезервированных восстанавливаемых ЭА основаны на предположении, что существует система контроля, которая выявляет все отказы, причем восстановление начинается немедленно. В действительности некоторая часть элементов сложного ЭА может быть не охвачена системой контроля; кроме того, контроль правильности работы части элементов сложного ЭА осуществляется во времени периодически (дискретно) при проведении ПНР. Поэтому значения показателей надежности будут хуже, чем в случае наличия идеальной системы контроля. Степень этого ухудшения значений показателей надежности можно оценить величиной
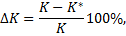
где К и К* — значения критериев соответственно при идеальной и реальной системе контроля.
Для ориентировочных расчетов ∆ К = 0,5...5,0%.
Так как в процессе эксплуатации сложного ЭА некоторые отказы система контроля может не выявить, то элементы сложного ЭА можно разделить на две группы: контролируемые и неконтролируемые с интенсивностями отказов 
и 
В этом случае функция готовности ЭА в целом будет равна произведению функций готовности этих двух групп и определяться по формуле
(6.22)
|
|
|
