Решение уравнений, описывающих вероятности состояний системы

Случай 1. Вероятности отказов и восстановлений заданы в виде функций интенсивностей. Тогда с достаточной для практических целей точностью можно принять

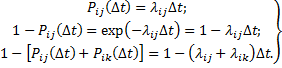(7.34)

Подставим (7.34) в (7.33), получим

(7.35)

Так как

то (7.35) приобретает вид

(7.36)

Существует правило, позволяющее записывать уравнение вида (7.36) непосредственно по графу состояния: в левой части уравне­ния записать (где P_k(t)— вероятность k -го состояния) и в правой части столько членов, сколько стрелок связано с данным состоянием. Если стрелка направлена в данное состояние, то ста­вится плюс, если из данного состояния, — минус. Каждый член равен плотности вероятности потока событий λ,переводящего сис­тему по данной стрелке, умноженной на вероятность того реше­ния, из которого исходит стрелка.

Решение системы уравнений (7.36) можно провести с исполь­зованием преобразования Лапласа. Это позволяет преобразовать систему дифференциальных уравнений в систему алгебраических.

В качестве примера расчета надежности восстанавливаемого объекта с использованием графа перехода рассмотрим ЭА, изобра­женный на рис. 7.14.

Запишем систему дифференциальных уравнений (5.21):

(7.37)

Произведем переход к изображениям по Лапласу и определим

Для того чтобы привести выражение 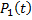к табличному, умножим и разделим правую часть на постоянную величину В результате получим

(7.38)

т. е. мы получили выражение (6.18). Правая часть формулы (7.38) состоит из постоянной и убывающей с течением времени частей. Постоянную часть называют стационарным коэффициентом го­товности.

Расчет надежности, связанный с решением дифференциальных уравнений, весьма трудоемок, особенно если его вести вручную. Поэтому существуют приемы, упрощающие расчет.

Исследования характеристик надежности, формируемых под воздействием потока отказов и восстановления, позволяют сделать вывод о том, что при существующих соотношениях λ и μ. сравни­тельно быстро наступает период установившегося режима, когда вероятности состояний объекта становятся постоянными, т. е. Тогда система дифференциальных уравнений (7.36) становится системой алгебраических уравнений. Например, сис­тема уравнений (7.37) трансформируется в следующую систему алгебраических уравнений:

(7.39)

 

Решив систему (7.39), получаем установившийся коэффици­ент готовности

Граф переходов с учетом восстановления в общем случае пред­ставлен на рис. 7.15.

Для облегчения расчетов можно пользоваться следующим пра­вилом. Если состояния заданы графом, имеющим вид рис. 7.15, тогда расчет надежности производится в следующей последова­тельности.

1. Записать уравнения состояний для каждого состояния по правилу: в левой части написать нуль, в правой части — столько членов, сколько стрелок связано с данным состоянием (каждой стрелке должно соответствовать слагаемое, представляющее со­
бой произведение интенсивности перехода на вероятность того состояния, из которого происходит переход; выходящей стрелке соответствует минус, входящей — плюс).

2. Вероятности каждого из состояний определяют выражениями

(7.40)

Запись для вероятности k -го состояния в (7.40) следует чи­тать так: вероятность k -го состояния равна произведению коэф­фициента на вероятность первого состояния Р₁. Коэффициент равен дроби, числитель которой — произведение интенсивностей отказов, стоящих над стрелками, идущими вправо до k -гo состоя­ния, а знаменатель — произведение интенсивностей восстанов­лений, стоящих над стрелками, идущими влево от k -гo состоя­ния до первого.

Случай 2. Характеристики отказов и восстановлений заданы вероятностями отказа Q(t)и восстановления Р_В (τ). В этом случае выражение для вероятности работоспособного состояния записы­вается следующим образом:

т. е. вероятность безотказного состояния за время t + τ с учетом восстановления равна вероятности отсутствия отказов за время t плюс вероятность восстановления за время t при условии, что за время t произошел отказ.

 

⇐ Предыдущая24252627282930313233Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: