 |
Средняя наработка до отказа восстанавливаемой системы
|
|
|
|
Средняя наработка до отказа

преобразование Лапласа для P(t):
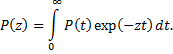
Отсюда ТСР = P (z)при z = 0. Преобразование Лапласа для dP (t)/ dt:

Если преобразовать (7.36) при z = 0 и учесть, что вероятность начального состояния при
t = 0 равна единице, а вероятности всех других состояний при t = 0 — нулю, получим следующие уравнения для времени пребывания системы в каждом из работоспособных состояний для графа состояний (см. рис. 7.12):

Правило написания уравнений для определения средней наработки до отказа восстанавливаемого объекта следующее: после того как получены уравнения для нахождения объекта в каждом из возможных работоспособных состояний, в левой части первого уравнения (для исходного состояния) ставится минус единица, во всех уравнениях вместо вероятностей — время пребывания объекта в этих состояниях. Решением полученной новой системы уравнений определяется TCPi. Сумма TCPiравна значению средней наработки до отказа системы.
Желающим познакомиться с расчетом надежности объекта при скользящем резервировании и учете последействия отказов рекомендуем обратиться к книге В. А. Острейковского [11]. Авторы не знают примеров такого вида резервирования для электрических аппаратов самой большой сложности.
РЕКОМЕНДУЕМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧИ И УПРАЖНЕНИЯ
ПРИНЦИПЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ
ПРИ РАСЧЕТЕ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
РЕЗЕРВИРОВАННЫХ СИСТЕМ
Задача 1. Дана система, схема расчета надежности которой изображена на рис. 7.16.
Необходимо найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов (значения вероятностей указаны на рис. 7.16)
Решение.
Из рис. 7.16 следует, что объект состоит из двух неравнонадежных устройств (1, 2). Устройство 1состоит из четырех узлов: А — дублированный узел с постоянно включенным резервом, причем каждая часть узла состоит из трех последовательно соединенных (в смысле надежности) элементов расчета; Б — дублированный узел по способу замещения; В — узел с одним нерезервированным элементом; Г — резервированный узел с кратностью т = 0,5 (схема группирования).
|
|
|

Устройство 2 представляет собой нерезервированное устройство, надежность которого известна. Так как оба устройства неравнонадежны, то вероятность безотказной работы всего объекта:

Найдем вероятность Pi(t).Вероятность безотказной работы устройства 1равна произведению вероятностей безотказной работы всех узлов, т.е.

В узле А используется общее резервирование кратности т = 1. При этом число элементов основной и резервной цепей равно трем, т. е. п = 3. Следовательно,

В узле Б кратность резервирования замещением т = 1. Тогда вероятность безотказной работы узла Б вычисляется по формуле

Для вычисления величины  использовано разложение в ряд Тейлора:
использовано разложение в ряд Тейлора:

В узле Г применено резервирование с дробной кратностью, когда общее число основных и резервных блоков l = 3, число блоков, необходимых для нормальной работы (основных), h = 2; тогда вероятность безотказной работы этого узла
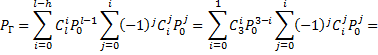

Теперь можно вычислить вероятность безотказной работы устройства 1:

тогда вероятность безотказной работы всего резервированного объекта будет вычисляться следующим образом:



Задача 2. Для повышения надежности электронной схемы все конденсаторы зарезервированы путем последовательного их соединения, как показано на рис. 7.17.
Необходимо найти вероятность безотказной работы соединения, если известно, что интенсивность отказов конденсатора λ = 0,3 • 10-6 1/ч, а вероятность возникновения отказов типа обрыва φ0 = 0,02. Предполагается, что электронная схема не критична к изменению емкости цепи конденсаторов и последействие отсутствует.
|
|
|
Решение.
Благоприятные ситуации, не приводящие к отказу схемы рис. 7.18, возникают в том случае, если А — не откажет ни один из конденсаторов; Б — пробит один любой конденсатор; В — пробиты два любых конденсатора, а один исправен.
Принимая эти ситуации за гипотезы, найдем вероятность их появления.
Вероятность того, что не откажет ни один из конденсаторов, будет равна произведению вероятностей p(t)безотказной работы всех трех конденсаторов, т. е. 
Вероятность, что два конденсатора исправны, а один пробит, равна p2qП. Но вероятность пробоя конденсатора qП равна произведению вероятности того, что отказ возникнет, на вероятность того, что возникший отказ будет типа пробоя, т. е. 
Так как в схеме три конденсатора, то возможен пробой любого из них, поэтому вероятность гипотезы Б

Вероятность того, что пробиты два конденсатора, а один исправен, равна  но так как по-прежнему
но так как по-прежнему  и таких ситуаций в схеме возможно ровно
и таких ситуаций в схеме возможно ровно  , то
, то

Суммируя вероятности всех гипотез, получим

Так как
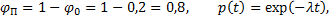
то очевидно, что


Выигрыш надежности по вероятности отказа будет
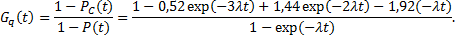
|
|
|


