Расчет надежности восстанавливаемых резервируемых систем

Задача 3. Система электроснабжения постоянным током со­стоит из трех источников напряжения: промышленной сети с пре­образователем переменного тока в постоянный, автономного мало­мощного источника и аккумуляторной батареи. При исправной промышленной сети потребители снабжаются электроэнергией только от преобразователя. При отказе промышленной сети или преобразователя подключается автономный маломощный источник совместно с буферной батареей. Система электроснабжения не обес­печивает питанием потребителей в том случае, если все три источ­ника отказали или отказала сеть и автономный источник системы электроснабжения (одна аккумуляторная батарея не может обес­печить питанием потребителя). Необходимо найти вероятность безотказной работы системы, если известны следующие данные:

— суммарная интенсивность отказов про­мышленной сети и преобразователя;

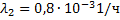— интенсивность отказов автономного источ­ника при совместной параллельной работе с аккумуляторной ба­тареей;

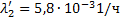— интенсивность отказов автономного источ­ника при отказе аккумуляторной батареи;

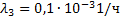— интенсивность отказа аккумуляторной ба­тареи при параллельной работе с автономным источником;

t = 100 ч — необходимое время непрерывной работы системы электроснабжения (потребители допускают перерыв в работе лишь на короткое время подключения автономного источника с акку­муляторной батареей в случае отказа сети).

До включения в работу автономный источник и аккумулятор­ная батарея отказать не могут

λ₂ = λ₃ = 0.

Задача 4. Для повышения надежности снабжения электроэнер­гией ответственного потребителя применена схема группирова­ния ЭА из 5 по 3. Требуется найти вероятность и среднюю нара­ботку до отказа системы, если интенсивность отказов каждого ЭА

последействие отсутствует, а время, в тече­ние которого система снабжения должна быть исправна, t = 500 ч.

Задача 5. Известны: λ — интенсивность отказов конденсато­ра; λ_о, λ_п = λ₁ — интенсивности отказов конденсатора соответст­венно по обрыву и пробою; φ₀ = λ₀/(λ₀ + λ₁)— вероятность того, что возникший отказ конденсатора произойдет из-за обрыва; t — вре­мя непрерывной работы схемы. Предполагается, что схемы не кри­тичны к изменению емкости цепи конденсаторов, последействие отказов отсутствует. Найти вероятность безотказной работы схем соединения конденсаторов, показанных на рис. 7.18.

Задача 6. На рис. 7.19 изображены две схемы резервирования диодов.

 

Известно, что интенсивность отказов диода λ 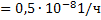, вероятность отказов типа «пробой» φ_п = 0,85, а время непрерыв­ной работы схемы t = 5000 ч. Предполагается, что последействие отказов отсутствует. Необходимо выяснить, какая схема лучше и какой выигрыш надежности по G_q она дает.

Задача 7. В системе телеконтроля могут быть применены схе­мы резервирования с дробной кратностью каналов 2 из 3 или 3 из 5. Интенсивность отказов одного канала λ 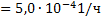. Требуется определить, какая схема имеет большую вероятность безотказ­ной работы в течение наработки до отказа.

Задача 8. В системе управле­ния, логическая схема которой изображена на рис. 7.20, приме­нено резервирование с дробной кратностью по схеме 2 из 3 измерительного устройства и пассив­ное резервирование с неизменной нагрузкой усилителя преобра­зователя.

Известны интенсивности отказов нерезервированного измери­теля 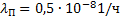, нерезервированного усилителя преобразо­вателя λ_У 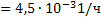и сервопривода

. Требует­ся рассчитать вероятность безотказной работы системы в течение наработки t = 50 ч.

Задача 9. Устройство состоит из (k + 1) параллельно соединен­ных равнонадежных блоков, вероятность безотказной работы каж­дого из которых P(t) = exp(-λt) = 0,85. Резерв пассивный с неизмен­ной нагрузкой. Определить потребную кратность резервирования, чтобы вероятность безотказной работы была не ниже заданной Р_зад = 0,98.

Задача 10. Устройство обработки информации состоит из трех одинаковых блоков. Вероятность безотказной работы устройства P_У(t) в течение наработки (0, t)должна быть не менее 0,9. Опреде­лить, какова должна быть вероятность безотказной работы каж­дого блока в течение наработки (0, t)для случаев: а) резерв отсут­ствует; б) имеется пассивный общий резерв с неизменной нагруз­кой всего устройства в целом; в) имеется пассивный раздельный резерв с неизменной нагрузкой по блокам.

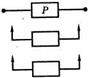
Задача 11. Определить вероятность безотказной работы систе­мы в течение наработки 10 ч. Структурная схема системы пред­ставлена на рис. 7.21, а блоки имеют следующие значения вероят­ностей безотказной работы: P₁(10) = 0,8; Р ₂(10)= 0,9; Р₃(10) = 0,95.

Задача 12. Определить вероятность безотказной работы систе­мы, структурная схема которой представлена на рис. 7.22, в тече­ние 50 ч непрерывной работы.

Вероятности безотказной работы блоков соответственно рав­ны Р₁(50) = 0,85; Р₂(50) - 0,8; P₃(50)= 0,95.

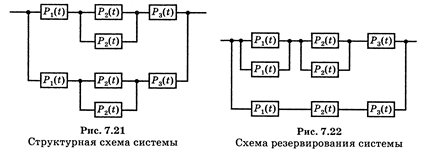
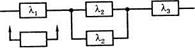
Рис. 7.23

Схема расчета надежности

Задача 13. Схема расчета надежности ЭА приведена на рис. 7.23. Необходимо найти интенсивность отказов уставки по перегруз­ке λ _сЭА при t = 0 и t = 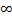, если первый элемент имеет ненагруженный активный резерв, а второй — нагруженный пассивный резерв.

Задача 14. Предложены следующие три системы электроснабже­ния промышленной сети:

а) один генератор мощностью 300 000 кВт; б) три генератора, каждый мощностью 100 000 кВт; в) пять гене­раторов, каждый мощностью 6000 кВт. Какая система электро­снабжения более надежна, если она не допускает восстановления и перерыва в работе и предназначена для непрерывной работы в течение t = 1000 ч? Интенсивности отказов генераторов растут пропорционально убыванию их мощности. Интенсивность отка­зов генератора мощностью

300 000 кВт 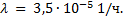Предпо­лагается, что в системе электроснабжения б) допустим отказ од­ного генератора, а в системе в) — двух генераторов.

Задача 15. Какая из систем электроснабжения, указанных в задаче 10, более надежна, если интенсивность отказов генерато­ров не зависит от мощности и составляет

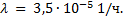
Задача 16. Две аккумуляторные батареи работают на одну на­грузку. Интенсивность отказов каждой из них 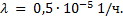При повреждении (отказе) одной из батарей интенсивность отказов исправной возрастает вследствие более тяжелых условий работы и равна Необходимо найти сред­нее время безотказной работы системы.

Задача 17. Схема расчета надежности ЭА при­ведена на рис. 7.24.

Рис. 7.24 Схема расчета надежности

Вероятность безотказной работы нерезервиро­ванного устройства в течение

t = 300 ч равна 0,74. Резерв ненагруженный и интенсивность отказов устройств λ = const. Необходимо найти его веро­ятность и среднее время безотказной работы.

Задача 18. Имеется дублированная система (два ЭА) при об­щем резервировании с постоянно включенным резервом. Интен­сивность отказов одного ЭА равна λ ₁а другого — λ ₂. При отказе первого ЭА интенсивность отказов второго возрастает и становится равной λ'₂ >λ₂, при отказе второго ЭА интенсивность отказов первого также возрастает и становится λ'₁ >λ₁. Требуется полу­чить формулу для вероятности безотказной работы системы Р_C(t) и средней наработки до отказа системы Т_СРс.

 

⇐ Предыдущая26272829303132333435Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: