 |
Погрешность простейших функций двух переменных.
|
|
|
|
ЧИСЛЕННЫЕ МЕТОДЫ
УЧЕБНОЕ ПОСОБИЕ
МОСКВА 2003
ББК 32.849+32.973-04
П18
УДК 396.62+681.327.8
Рецензенты:
П18 Куликов С.П., Самохин А.Б., Чердынцев В.В. Численные методы: Учебное пособие / Московский государственный институт радиотехники, электроники и автоматики (технический университет) – М., 2003. – 108с.
ISBN 5-7339-0211-6
Рассмотрены некоторые численные методы решения прикладных математических задач. Учебное пособие написано для студентов, обучающихся по математическим специальностям факультета кибернетики. Оно может быть полезным также при изучении дисциплин “Математическое моделирование” и “Методы оптимизации”.
Табл.3, Ил.60, Библиогр.: 7 назв.
Печатается по решению редакционно-издательского совета Московского государственного института радиотехники, электроники и автоматики (технического университета).
 Без объявл. ББК 32.849+32.973-04
Без объявл. ББК 32.849+32.973-04
ISBN 5-7339-0211-6
© С.П. Куликов,
А.Б. Самохин,
В.В. Чердынцев.
Введение
Вычислительные задачи, возникающие при инженерных исследованиях, разбиваются на ряд элементарных. В настоящем курсе рассмотрены некоторые классические задачи вычислительной математики. Для многих задач существует несколько методов решения и выбор оптимального требует определенного опыта, поэтому особое внимание уделено изложению алгоритмов.
Настоящее пособие является введением в численные методы. В конце каждой темы приведены задания для практических занятий, выполнение которых позволяет лучше усвоить вычислительные алгоритмы. При их решении допустимо использование инженерных калькуляторов и крайне нежелательно применение математических пакетов прикладных программ.
|
|
|
Абсолютная и относительная погрешности.
Численные методы, служат для нахождения приближенного решения математических задач. Любое приближенное решение связано с ошибкой (погрешностью). Виды ошибок:
1. Погрешность математической модели, связанная с неполными знаниями о процессе.
2. Погрешность упрощения модели.
3. Погрешность, связанная с приближенным характером начальных данных.
4. Погрешность округления при расчетах.
Первые две погрешности относятся к систематическим, а две последние - к статистическим ошибкам. Для их оценки вводится абсолютная и относительная погрешности.
Абсолютная (предельная) погрешность – определяет интервал, в котором лежит точное значение величины.
Пусть А - точное значение величины (неизвестно), а а - приближенное значение величины (известно). За абсолютную погрешность  принимается минимальное число
принимается минимальное число  ,
,  удовлетворяющее условию:
удовлетворяющее условию:
 (1.1)
(1.1)
При статистических измерениях погрешность  задается с определенной достоверностью, т.е. вероятность события
задается с определенной достоверностью, т.е. вероятность события  больше определенной величины
больше определенной величины  . Перепишем определение:
. Перепишем определение:  ; то есть точное значение
; то есть точное значение  лежит в заданном интервале. Для оценки качества измерений вводится относительная погрешность:
лежит в заданном интервале. Для оценки качества измерений вводится относительная погрешность:

 . (1.2)
. (1.2)
Заданные величины  или
или  позволяют записать точное значение А в символическом виде:
позволяют записать точное значение А в символическом виде:  или
или  .
.
1..1 Число верных знаков приближенного числа.
Приближенное число можно представить в виде:
 , (1.3)
, (1.3)
где m - величина старшего разряда, n - текущий номер знака, отсчитываемый слева направо. Говорят, что n первых знаков приближенного числа верные, если абсолютная погрешность  удовлетворяют условию:
удовлетворяют условию:  , то есть меньше половины соответствующего разряда. Подбирается минимальное число вида 0,5×10к большее,
, то есть меньше половины соответствующего разряда. Подбирается минимальное число вида 0,5×10к большее,  и сравниваются разряды.
и сравниваются разряды.
Погрешность функций
Пусть дана функция  от n приближенных значений
от n приближенных значений  , погрешности которых известны. Требуется определить погрешность функции
, погрешности которых известны. Требуется определить погрешность функции  .
.
 , где
, где  - абсолютная погрешность приближенной величины
- абсолютная погрешность приближенной величины  . Если
. Если  , то разность, стоящую в формуле можно оценить в линейном приближении:
, то разность, стоящую в формуле можно оценить в линейном приближении:
|
|
|

Отсюда следует оценка погрешности:
 ,
,  (1.4)
(1.4)
Погрешность простейших функций двух переменных.
Погрешность суммы:

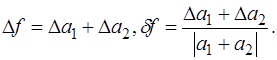
Погрешность разности:

При  качество измерений разности ухудшается.
качество измерений разности ухудшается.
Замечание: Абсолютная погрешность суммы и разности n приближенных величин равна сумме их абсолютных погрешностей.
Погрешность произведения:



То есть предпочтительней сначала найти относительную погрешность, а затем искать абсолютную: 
Замечания:
· Относительная погрешность степени есть произведение модуля показателя на относительную погрешность основания степени:  .
.
· Относительная погрешность произведения n сомножителей приближенных величин равна сумме относительных погрешностей сомножителей:

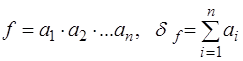 .
.
Погрешность частного:


Все замечания сделанные для произведения справедливы и в этом случае.
Примеры и задания.
Пример: дано приближенное число 3457,0погрешность - 0,6. Найти число верных знаков. Цифра 3 входит в число с весом 103, (1.3) то есть m =3.  , минимальное k =1,
, минимальное k =1,  , то есть верны три знака
, то есть верны три знака 
Пример: Дан куб, сторона которого  , измерена с точностью
, измерена с точностью  . Определить погрешности измерения поверхности и объема куба:
. Определить погрешности измерения поверхности и объема куба:



Пример. Расчет погрешности функции трех переменных (1.4):

 ,
, 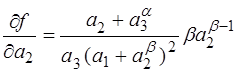 ,
,  .
.
 .
.
Пример. Катеты прямоугольного треугольника  см. и
см. и  см. измерены с погрешностью
см. измерены с погрешностью  см. Определить погрешность измерения гипотенузы с.
см. Определить погрешность измерения гипотенузы с.
 см.,
см.,  ,
,  ,
,  см.
см.
В каждом варианте задания три задачи, ниже приведены последовательно первая, вторая и третья задачи вариантов.
А. Найти абсолютную и относительную ошибки выражения, где  ,
,  и
и  - приближенные величины данные с погрешностями
- приближенные величины данные с погрешностями  - соответственно:
- соответственно:
1)  ,
,  . 2)
. 2) 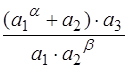 ,
, 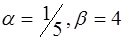 .
.
3)  ,
, 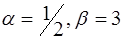 .
.
4)  ,
,  .
.
5)  ,
, 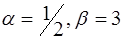 . 6)
. 6) 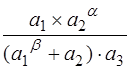 ,
, 
7) 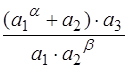 ,
,  . 8)
. 8)  ,
,  . 9)
. 9)  ,
, 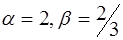 .
.
10) 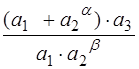 ,
,  . 11)
. 11)  ,
, 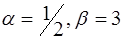 . 12)
. 12)  ,
,  .
.
13)  ,
, 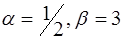 . 14)
. 14) 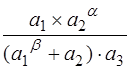 ,
,  .
.
15)  ,
,  . 16.
. 16.  ,
,  .
.
Б. Дано приближенное число и его погрешность. Найти количество верных знаков:
1) 23,587; 0,08. 2) 13,58; 0,07. 3) 103,58; 0,03. 4) 1655; 6.
5) 323,07; 0,06. 6) 43,837; 0,008. 7) 16,402; 0,009. 8) 13,540; 0,006.
9) 31,541; 0,003. 10) 13,42; 0,03. 11) 137,5; 0,08. 12) 134; 20.
13) 3457,0; 0,6. 14) 4657; 8. 15) 16,47; 0,07. 16) 130,6; 0,06.
В. Дана геометрическая фигура. Определить в трехмерном случае объем и полную поверхность, а в плоском случае площадь и периметр. Погрешность определения размеров линейных элементов равна 1см:
|
|
|
1) Равнобедренная трапеция со сторонами основания, равными 20 и 30см. и высотой равной 12см.
2) Правильная четырехугольная пирамида со стороной основания равной 10см. и высотой равной 12см.
3) Конус с высотой равной 30см. и радиусом равным 40см.
4) Прямоугольный параллелепипед с высотой 30см стороной основания 60см и диагональю основания 100см.
5) Цилиндр с главной диагональю равной 100см. и радиусом равным 40см.
6) Равнобедренная трапеция со сторонами основания, равными 20 и 80см. и высотой равной 40см.
7) Правильная четырехугольная пирамида со стороной основания равной 60см. и высотой равной 40см.
8) Прямоугольный параллелепипед с высотой 25см, стороной основания 60 и диагональю основания 100см.
9) Равнобедренная трапеция со сторонами основания, равными 34 и 58см. и высотой равной 5см.
10) Правильная четырехугольная пирамида со стороной основания равной 120см. и высотой равной 80см.
11) Конус с высотой равной 12см. и радиусом основания, равным 5см.
12) Прямоугольный параллелепипед с высотой 20см стороной основания 50 и диагональю основания 130см.
13) Цилиндр с образующей равной 60см. и главной диагональю равной 100см.
14) Равнобедренная трапеция со сторонами основания, равными 20 и 32см. и высотой равной 8см.
15) Правильная четырехугольная пирамида со стороной основания равной 24см. и высотой равной 5см.
16) Прямоугольный параллелепипед со стороной основания 12см, его диагональю 13см и высотой 40см.
Приближение функций
Во многих случаях функция задается таблично, то есть, известны её значения только в узловых точках (узлах):
Таблица 2.1

Необходимо построить функцию, приблизительно описывающую зависимость между узлами. Приближающая функция обычно берется в виде суммы элементарных функций. На практике используются степенные, показательные, тригонометрические функции. В дальнейшем будем рассматривать полиномиальное приближение, т.е. приближающая функция имеет вид:
 .
.
|
|
|
Существуют два основных критерия (условия) построения приближающих функций. Критерий интерполяции требует, чтобы приближающая функция проходила через узлы. Критерий аппроксимации требует минимизации некоторого функционала.
|
|
|


